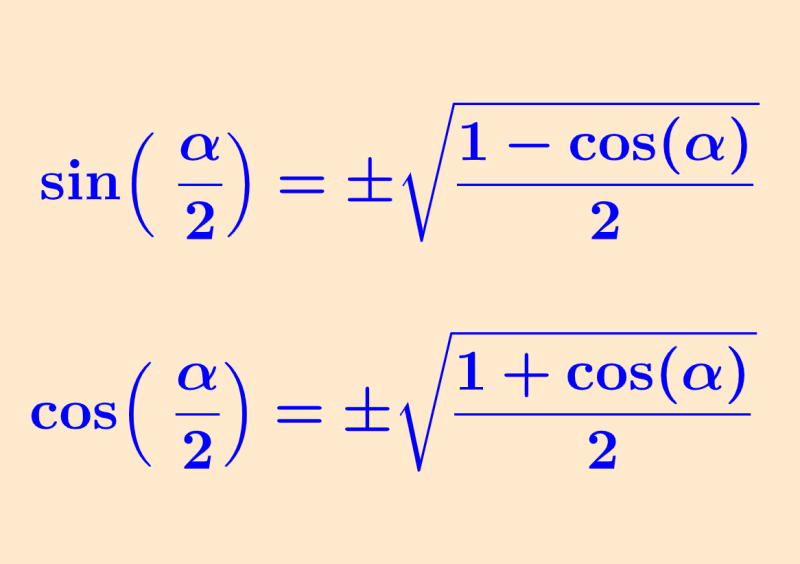Las identidades de ángulos medios son identidades trigonométricas usadas para simplificar expresiones trigonométricas y calcular el seno, coseno o tangente de ángulos medios cuando conocemos los valores de un ángulo dado. Estas identidades son obtenidas usando las identidades de ángulos dobles y realizando una sustitución.
A continuación, aprenderemos a derivar las identidades de ángulos medios y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cuáles son las identidades de ángulos medios?
Las identidades de ángulos medios son identidades trigonométricas que son usadas para calcular o simplificar expresiones con ángulos medios, como $latex \sin(\frac{\theta}{2})$. Estas identidades también pueden ser usadas para transformar expresiones trigonométricas con exponentes a una sin exponentes.
La identidad de ángulo medio del seno es:
| $latex \sin(\frac{\theta}{2})=\pm \sqrt{\frac{1-\cos(\theta)}{2}}$ |
La identidad de ángulo medio del coseno es:
| $latex \cos(\frac{\theta}{2})=\pm \sqrt{\frac{1+\cos(\theta)}{2}}$ |
La identidad de ángulo medio de la tangente es:
| $latex \tan(\frac{\theta}{2})=\frac{\sin(\theta)}{1+\cos(\theta)}$ $latex =\frac{1-\cos(\theta)}{\sin(\theta)}$ |
¿Cómo derivar las identidades de ángulos medios?
Las identidades de ángulos medios pueden ser derivadas usando las indentidades de ángulos dobles.
Para derivar la fórmula de la identidad de ángulo medio de senos, empezamos con la identidad de ángulos dobles de cosenos:
$latex \cos(2\theta)=1-2{{\sin}^2}(\theta)$
Si es que usamos la relación $latex \theta=\frac{\alpha}{2}$, tenemos $latex 2\theta=\alpha$. Sustituyendo estas expresiones en la identidad de arriba, tenemos:
$latex \cos(\alpha)=1-2{{\sin}^2}(\frac{\alpha}{2})$
Ahora, resolvemos esta expresión para $latex \sin(\frac{\alpha}{2})$:
$latex \cos(\alpha)=1-2{{\sin}^2}(\frac{\alpha}{2})$
$latex 2{{\sin}^2}(\frac{\alpha}{2})=1-\cos(\alpha)$
$latex {{\sin}^2}(\frac{\alpha}{2})=\frac{1-\cos(\alpha)}{2}$
$latex \sin(\frac{\alpha}{2})=\pm\sqrt{\frac{1-\cos(\alpha)}{2}}$
El signo de $latex \sin(\frac{\alpha}{2})$ depende del cuadrante en el que $latex \frac{\alpha}{2}$ se ubique. Si es que $latex \frac{\alpha}{2}$ está en el primer o segundo cuadrante, la fórmula usa el signo positivo y si es que $latex \frac{\alpha}{2}$ está en el tercer o cuarto cuadrante, la fórmula usa el signo negativo.
Usamos un proceso similar para encontrar la identidad de ángulo medio de coseno. Entonces, empezamos con la identidad de doble ángulo del coseno en la siguiente forma:
$latex \cos(2\theta)=2{{\cos}^2}(\theta)-1$
Luego de realizar las sustituciones, obtenemos:
$latex \cos(\alpha)=2{{\cos}^2}(\frac{\alpha}{2})-1$
Ahora, resolvemos para $latex \cos(\frac{\alpha}{2})$:
$latex \cos(\alpha)=2{{\cos}^2}(\frac{\alpha}{2})-1$
$latex 2{{\cos}^2}(\frac{\alpha}{2})=1+\cos(\alpha)$
$latex {{\cos}^2}(\frac{\alpha}{2})=\frac{1+\cos(\alpha)}{2}$
$latex \cos(\frac{\alpha}{2})=\pm\sqrt{\frac{1+\cos(\alpha)}{2}}$
En este caso, si es que $latex \frac{\alpha}{2}$ está en el primer o cuarto cuadrante, la fórmula usa el signo positivo y si es que $latex \frac{\alpha}{2}$ está en el segundo o tercer cuadrante, la fórmula usa el signo negativo.
Ejercicios de identidades de ángulos medios resueltos
Los siguientes ejercicios son resueltos usando lo aprendido sobre las identidades de ángulos medios. Estudia y analiza estos ejercicios para entender el proceso usado.
EJERCICIO 1
Usa la identidad de ángulo medio del seno para encontrar el valor de seno de 15°.
Solución
Usamos la fórmula de la identidad del ángulo medio del seno con el valor dado. Entonces, tenemos:
$latex \sin(\frac{\theta}{2})=\pm\sqrt{\frac{1-\cos(\theta)}{2}}$
$latex \sin(15^{\circ})=\pm\sqrt{\frac{1-\cos(30^{\circ} )}{2}}$
$latex =\pm\sqrt{\frac{1-0.866}{2}}$
$latex =0.259$
Usamos el valor positivo ya que 15° está en el primer cuadrante.
EJERCICIO 2
Determina el valor del coseno de 165° usando la identidad del ángulo medio del coseno.
Solución
Para usar la identidad del ángulo medio del coseno, usamos el ángulo $latex \frac{\theta}{2}=165$°. Esto significa que tenemos $latex \theta=330$°. Entonces, usamos la fórmula con estos valores:
$latex \cos(\theta)=\pm\sqrt{\frac{1+\cos(\theta)}{2}}$
$latex \cos(165^{\circ})=\pm\sqrt{\frac{1+\cos(330^{\circ})}{2}}$
$latex =\pm\sqrt{\frac{1+0.866}{2}}$
$latex =-0.966$
Escogimos el valor negativo, ya que el ángulo 165° está en el segundo cuadrante.
EJERCICIO 3
Comprueba que la identidad $latex 2{{\sin}^2}(\frac{x}{2})+\cos(x)=1$.
Solución
Podemos usar la identidad del ángulo medio del seno para reemplazar y simplificar la expresión. Al realizar esto, tenemos:
$latex 2{{\sin}^2}(\frac{x}{2})+\cos(x)$
$latex =2{{(\sqrt{\frac{1-\cos(x)}{2}})}^2}+\cos(x)$
$latex =2(\frac{1-\cos(x)}{2})+\cos(x)$
$latex =1-\cos(x)+\cos(x)$
$latex =1$
Después de simplificar, vemos que el lado izquierdo de la identidad es igual al lado derecho, por lo que la identidad sí es verdadera.
Ejercicios de identidades de ángulos medios para resolver
Resuelve los siguientes ejercicios de práctica usando lo aprendido sobre las identidades de ángulos medios de seno, coseno y tangente. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
