Los polinomios son expresiones algebraicas que contienen variables y coeficientes junto con operaciones matemáticas como adición, sustracción y multiplicación. Podemos realizar operaciones matemáticas similar a como realizamos operaciones con expresiones algebraicas.
A continuación, veremos un resumen de los polinomios y sus operaciones matemáticas. Luego, veremos varios ejercicios de polinomios resueltos para aprender a realizar estas operaciones con polinomios.
Resumen de polinomios
Los polinomios son expresiones algebraicas que consisten de variables, constantes y exponentes que son combinados usando las operaciones matemáticas como adición, sustracción y multiplicación.
Basado en el número de términos en la expresión, los polinomios pueden ser clasificados como monomio, binomio, trinomio y otros. Los siguientes son ejemplos de variables, constantes y exponentes:
- Constantes: 1, 2, 3, etc.
- Variables: a, b, x, y, etc.
- Exponentes: el 2 en $latex {{x}^2}$.
Una función polinomial usualmente es representada por $latex P(x)$, en donde, x es la variable.
Podemos realizar varias operaciones matemáticas con polinomios. Veamos un resumen de adición, sustracción y multiplicación de polinomios.
Adición de polinomios
Para sumar polinomios, simplemente tenemos que combinar términos semejantes. Recordemos que los términos semejantes son términos que tienen las mismas variables elevadas a las mismas potencias.
La adición de polinomios siempre resulta en un polinomio del mismo grado.
Sustracción de polinomios
Sustracción de polinomios es similar a la adición con la diferencia que tenemos un cambio de signos. Entonces, restamos los términos semejantes para obtener la solución.
La sustracción de polinomios también resulta en un polinomio del mismo grado.
Multiplicación de polinomios
Para multiplicar polinomios, tenemos que usar la propiedad distributiva para multiplicar a todos los términos. La propiedad distributiva es:
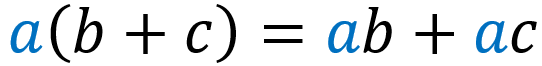
Cuando multiplicamos a dos o más polinomios, siempre obtenemos un polinomio con un grado más grande, a menos que uno de los polinomios sea una constante.
Ejercicios de polinomios resueltos
Los siguientes ejercicios detallan el proceso usado para realizar operaciones matemáticas con polinomios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra la suma de los polinomios: $latex (4{{x}^2}+5)+(3{{x}^2}+4)$.
Solución
Para sumar los polinomios, tenemos que combinar términos semejantes. Entonces, combinamos a los términos con $latex {{x}^2}$ y los términos constantes separadamente:
$latex (4{{x}^2}+5)+(3{{x}^2}+4)$
$latex =7{{x}^2}+9$
EJERCICIO 2
Encuentra la diferencia de los polinomios: $latex (2{{x}^3}+4{{x}^2}+4)-(3{{x}^3}+2{{x}^2}+2)$.
Solución
En este caso, tenemos que restar los términos semejantes. Comparamos todos los términos que son semejantes:
$latex (2{{x}^3}+4{{x}^2}+4)-(3{{x}^3}+2{{x}^2}+2)$
$latex =2{{x}^3}-3{{x}^3}+4{{x}^2}-2{{x}^2}+4-2$
$latex =-{{x}^3}+2{{x}^2}+2$
EJERCICIO 3
Realiza la suma de polinomios: $latex (3{{x}^5}+8{{x}^4}-4{{x}^3}+2{{x}^2}-5x+2)$ $latex +(4{{x}^5}-4{{x}^4}-2{{x}^3}+5{{x}^2}+3x+10)$.
Solución
En este caso, tenemos varios términos con diferentes variables y signos diferentes. Sin embargo, tenemos que aplicar la misma idea. Identificamos términos semejantes y los combinamos:
$latex (3{{x}^5}+8{{x}^4}-4{{x}^3}+2{{x}^2}-5x+2)$ $latex +(4{{x}^5}-4{{x}^4}-2{{x}^3}+5{{x}^2}+3x+10)$
$latex =7{{x}^5}+4{{x}^4}-6{{x}^3}+7{{x}^2}-2x+12$
EJERCICIO 4
Realiza la sustracción de polinomios: $latex (2{{x}^5}y+4{{x}^4}-3{{x}^3}+5{{x}^2}y-5x+2)$ $latex -(6{{x}^5}-4{{x}^4}+2{{x}^3}+2{{x}^2}+3x-5)$.
Solución
Este polinomio tiene términos con la variable y, los cuales no tienen términos semejantes. Entonces, tenemos que combinar solo los términos semejantes y simplemente copiamos los términos que no tienen términos semejantes:
$latex (2{{x}^5}y+4{{x}^4}-3{{x}^3}+5{{x}^2}y-5x+2)$ $latex -(6{{x}^5}-4{{x}^4}+2{{x}^3}+2{{x}^2}+3x-5)$
$latex =2{{x}^5}y-6{{x}^5}+(4+4){{x}^4}+(-3-2){{x}^3}$ $latex +5{{x}^2}y-2{{x}^2}+(-5-3)x+2+5$
$latex =2{{x}^5}y-6{{x}^5}+8{{x}^4}-5{{x}^3}$ $latex +5{{x}^2}y-2{{x}^2}-8x+7$
EJERCICIO 5
Realiza la multiplicación de polinomios: $latex (4x+2)(3x-3)$.
Solución
Tenemos que usar la propiedad distributiva para distribuir y multiplicar a todos los términos. Entonces, tenemos:
$latex (4x+2)(3x-3)$
$latex =4x(3x-3)+2(2x-3)$
$latex =12{{x}^2}-12x+4x-6$
Ahora, sólo tenemos que combinar términos semejantes para simplificar:
$latex =12{{x}^2}-12x+4x-6$
$latex =12{{x}^2}-8x-6$
EJERCICIO 6
Multiplica los polinomios: $latex (2{{x}^2}+5x)(4{{x}^2}-2x+3)$.
Solución
Nuevamente, usamos la propiedad distributiva para multiplicar todos los términos del polinomio. Luego, simplificamos el resultado al combinar términos semejantes:
$latex (2{{x}^2}+5x)(4{{x}^2}-2x+3)$
$$=2{{x}^2}(4{{x}^2}-2x+3)+5x(4{{x}^2}-2x+3)$$
$$=8{{x}^4}-4{{x}^3}+6{{x}^2}+20{{x}^3}-10{{x}^2}+15x$$
$latex =8{{x}^4}+16{{x}^3}-4{{x}^2}+15x$
EJERCICIO 7
Obtén el resultado de la multiplicación de polinomios: $latex (5x^2-3x+2)(2x^2+4x-5)$.
Solución
Similar a los ejercicios anteriores, tenemos que usar la propiedad distributiva para multiplicar a todos los términos. Luego, simplificamos el resultado al combinar términos semejantes:
$latex (5x^2-3x+2)(2x^2+4x-5)$
$$=5x^2(2x^2+4x-5)-3x(2x^2+4x-5) +2(2x^2+4x-5)$$
$$=10{{x}^4}+20{{x}^3}-25{{x}^2}-6{{x}^3}-12{{x}^2} +15x+4{{x}^2}+8x-10$$
$latex =10{{x}^4}+14{{x}^3}-33{{x}^2}+23x-10$
Ejercicios de polinomios para resolver
Pon en práctica tu conocimiento sobre polinomios y tus habilidades para resolver operaciones con polinomios con los siguientes ejercicios. Si necesitas ayuda, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre polinomios y expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
