Podemos realizar varias operaciones con expresiones algebraicas. Estas operaciones incluyen adición, sustracción, multiplicación y división. En este artículo aprenderemos a realizar estas operaciones con expresiones algebraicas.
Miraremos varios ejemplos resueltos para entender completamente las ideas principales.
ÁLGEBRA
Relevante para…
Realizar adición, sustracción, multiplicación y división con expresiones algebraicas.
ÁLGEBRA
Relevante para…
Realizar adición, sustracción, multiplicación y división con expresiones algebraicas.
Orden de operaciones
Las operaciones con expresiones algebraicas siguen un cierto orden. Cada vez que veas una expresión algebraica o una ecuación, descomponla en el orden en el que tiene que ser resuelta. Para recordar fácilmente este orden, ten en cuenta este acrónimo: PEMDAS:
1. Evalúa todas las expresiones dentro de paréntesis u otros símbolos de agrupación.
2. Evalúa todas las expresiones que contengan exponentes.
3. Realiza las multiplicaciones y divisiones restantes a medida que te encuentras con ellas. Es decir, realiza las multiplicaciones y divisiones de izquierda a derecha.
4. Realiza las adiciones y sustracciones restantes a medida que te encuentras con ellas. Es decir, realiza las adiciones y sustracciones de izquierda a derecha.
EJEMPLOS
- Resuelve $latex 5+4\times 3$.
Solución: Aplica el orden de operaciones:
$latex 5+4\times 3=5+12=17$
- Resuelve $latex 2\left( {3+1} \right)+2\times 3\left( {3+1} \right)$.
Solución: Aplica el orden de operaciones:
$$2\left( {3+1} \right)+2\times 3\left( {3+1} \right)=2\left( 4 \right)+2\times 3\left( 4 \right)$$
$latex =8+2\times 12$
$latex =8+24$
$latex =32$
Inténtalo tú mismo – Resuelve el ejercicio
Adición y sustracción
En adición o sustracción de expresiones algebraicas, es importante que los términos sean términos semejantes. Los términos semejantes son definidos como las mismas variables elevadas a la misma potencia.
EJEMPLOS
- Suma las expresiones $latex 2x+4$ y $latex 3x+2$.
Solución: Identifica los términos semejantes y combínalos:
$latex 2x+4+3x+2=5x+6$
- Suma las expresiones $latex 2{{x}^{2}}+3x+4$ y $latex 4{{x}^{2}}-2x+3$ .
Solución: Identifica los términos semejantes y combínalos:
$latex 2{{x}^{2}}+3x+4+4{{x}^{2}}-2x+3$
$latex =6{{x}^{2}}+x+7$
- Resta la expresión $latex 3x+3$ de la expresión $latex 8x+5$.
Solución: Dado que es una resta, cambiamos de signo a la expresión que está restando:
$$8x+5-(3x+3)=8x+5-3x-3$$
$latex =5x+2$
- Resta la expresión $latex 2{{x}^{2}}+3x-6$ de la expresión $latex -4{{x}^{2}}+2x-5$.
Solución: Dado que es una resta, cambiamos de signo a la expresión que está restando:
$latex -4{{x}^{2}}+2x-5-\left( {2{{x}^{2}}+3x-6} \right)$
$latex =-4{{x}^{2}}+2x-5-2{{x}^{2}}-3x+6$
$latex =-6{{x}^{2}}-x+1$
Inténtalo tú mismo – Resuelve el ejercicio
Multiplicación
Para multiplicar expresiones algebraicas, tenemos que usar la propiedad distributiva. La propiedad distributiva indica que para cualesquier números reales $latex a, b, c$, tenemos:
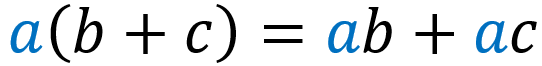
EJEMPLOS
- Multiplica $latex x$ por $latex x+1$.
Solución: Usamos la propiedad distributiva para distribuir la $latex x$:
$$x\left( {x+1} \right)=x\times x+x\times 1$$
$latex ={{x}^{2}}+x$
- Multiplica $latex x+2$ por $latex x+1$.
Solución: Usamos la propiedad distributiva dos veces, distribuimos la $latex x$ y luego el 2:
$$(x+2)(x+1)={{x}^{2}}+x+2x+2$$
$latex ={{x}^{2}}+3x+2$
- Multiplica $latex x+4$ por $latex {{x}^{2}}+2x-5$.
Solución: Usamos la propiedad distributiva dos veces, distribuimos la $latex x$ y luego el 4:
$latex (x+4)({{x}^{2}}+2x-5)$
$$={x}^{3}+2{{x}^{2}}-5x+4{{x}^{2}}+8x-20$$
$latex ={{x}^{3}}+6{{x}^{2}}+3x-20$
- Multiplica $latex x-3$ por $latex 2{{x}^{2}}-2x+3$.
Solución: Usamos la propiedad distributiva dos veces, distribuimos la $latex x$ y luego el -3:
$latex (x-3)(2{{x}^{2}}-2x+3)$
$$=2{x}^{3}-2{{x}^{2}}+3x-6{{x}^{2}}+6x-9$$
$latex ={2{x}^{3}}-8{{x}^{2}}+9x-12$
Inténtalo tú mismo – Resuelve el ejercicio
División
Dividir una expresión algebraica es similar a simplificar términos. Los coeficientes numéricos son divididos y los exponentes de las variables son sustraídos.
EJEMPLOS
- Divide $latex 6{{a}^{2}}{{b}^{3}}$ por $latex 2{{a}^{3}}{{b}^{2}}$.
Solución: Para entender más fácilmente, escribimos la división de la siguiente manera:
$$\frac{{6aa~bbb}}{{2~aaa~bb}}$$
Dividimos las constantes y simplificamos las variables:
$$=\frac{{3b}}{a}$$
- Resuelve lo siguiente:
$$\frac{{\left( {x+1} \right)\left( {x+2} \right)}}{{\left( {x+2} \right)\left( {x-3} \right)}}$$
Solución: Simplificamos la expresión algebraica al cancelar los términos:
$$\frac{{x+1}}{{x-3}}$$
- Simplificar la expresión $latex \frac{3}{x}+\frac{4}{{x+1}}$.
Solución: Para simplificar, la ecuación necesita tener el mismo denominador. Aquí, multiplicamos por $latex x\left( {x+1} \right)$ ambos términos y cancelamos:
$$\frac{{3\left( x \right)\left( {x+1} \right)}}{x}=3\left( {x+1} \right)$$
$$\frac{{4\left( x \right)\left( {x+1} \right)}}{{x+1}}=4x$$
Uniendo los términos y simplificando, tenemos:
$$3\left( {x+1} \right)+4x=3x+3+4x$$
$latex =7x+3$
Inténtalo tú mismo – Resuelve el ejercicio
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:


