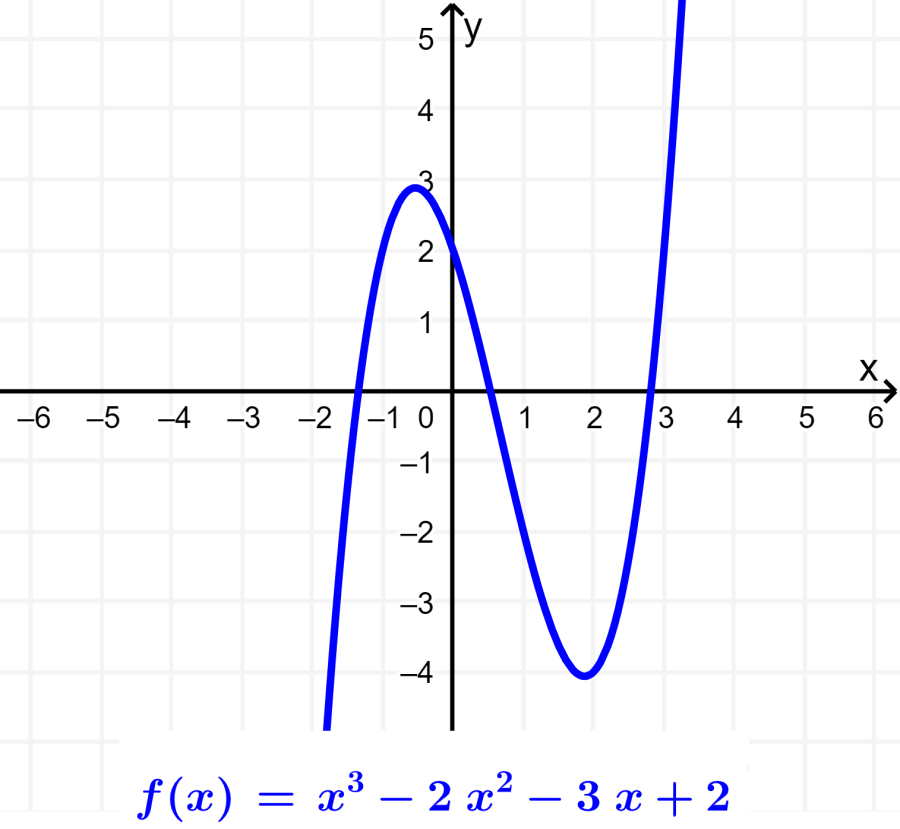
Las funciones polinomiales son funciones que solo tienen exponentes enteros no-negativos de la variable independiente. Algunos ejemplos de funciones polinomiales son la función lineal, la función cuadrática y la función cúbica. Las gráficas de estas funciones varían dependiendo del grado de la función.
A continuación, veremos un resumen sobre las funciones polinomiales junto con sus características más principales. Además, veremos varios ejercicios resueltos para aprender sobre sus características y sus aplicaciones.
Resumen de funciones polinomiales
Una función polinomial es una función tal como una cuadrática, cúbica, cuártica, entre otras, que solo tiene potencias enteras no-negativas de x. Un polinomio de grado n es una función que tiene la forma general:
$$f(x)=a_{n}{{x}^n}+a_{n-1}{{x}^{n-1}}+…+a_{2}{{x}^2}+a_{1}x+a_{0}$$
en donde, los coeficientes a son todos números reales. A pesar de que la forma general se ve muy complicada, los ejemplos particulares son más simples. Por ejemplo,
$latex f(x)=2{{x}^3}+4{{x}^2}+2x$
es una función polinomial de grado 3, ya que 3 es la potencia más grande de la función. Y la función:
$latex f(x)=-4{{x}^5}+2{{x}^4}+3{{x}^2}+6$
es una función polinomial de grado 5, ya que 5 es la potencia más grande de la función.
Raíces de funciones polinomiales
Cuando tenemos $latex (x-a)(x-b)=0$, sabemos que a y b son las raíces de la función $latex f(x)=(x-a)(x-b)$. Entonces, podemos encontrar las raíces polinomiales al formar una ecuación igualando con cero a la parte polinomial de la función y factorizar o resolver para x.
También es posible usar lo opuesto de esto. Por ejemplo, si es que tenemos que a y b son raíces, sabemos que la función polinomial con estas raíces debe ser $latex f(x)=(x-a)(x-b)$, o un múltiplo de esto.
Si es que $latex x=3$ y $latex x=-4$ son las raíces de la función polinomial, entonces, esta función debe ser $latex f(x)=(x-3)(x+4)$, o un múltiplo constante de esto.
→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas
Ejercicios de funciones polinomiales resueltos
Los siguientes ejercicios de funciones polinomiales pueden ser usados para aprender sobre las aplicaciones y los problemas más comunes que se pueden encontrar con estas funciones.
EJERCICIO 1
¿Es la función $latex f(x)=-2+3{{x}^2}+2{{x}^3}$ una función polinomial?
Solución
Podemos ver que la función $latex f(x)=-2+3{{x}^2}+2{{x}^3}$ solo tiene variables con exponentes enteros positivos, por lo tanto, esta función sí es polinomial.
EJERCICIO 2
¿Es la función $latex f(x)=-2{{x}^3}+5{{x}^2}+\sqrt{x}$ una función polinomial?
Solución
Teniendo en cuenta que los radicales pueden ser escritos como potencias fraccionarias, podemos escribir a la función $latex f(x)=-2{{x}^3}+5{{x}^2}+\sqrt{x}$ como:
$latex f(x)=-2{{x}^3}+5{{x}^2}+{{x}^{\frac{1}{2}}}$
Vemos que no todos los exponentes de la variable son números enteros positivos. Entonces, esta función no es una función exponencial.
EJERCICIO 3
Escribe una función polinomial que tiene raíces 2, 3, 5, 7.
Solución
Cuando tenemos a un polinomio escrito en la forma $latex (x-a)(x-b)=0$, sabemos que sus raíces son a y b.
Entonces, podemos encontrar un polinomio factorizado al conocer esas raíces. En este caso, las raíces son 2, 3, 5, y 7, por lo que tenemos:
$latex f(x)=(x-2)(x-3)(x-5)(x-7)$
Esto significa que la función polinomial que tiene las raíces dadas es $latex f(x)=(x-2)(x-3)(x-5)(x-7)$ o un múltiplo de este polinomio.
Por ejemplo, $latex f(x)=2(x-2)(x-3)(x-5)(x-7)$ y $latex f(x)=-5(x-2)(x-3)(x-5)(x-7)$ también son funciones polinomiales que tienen las raíces dadas.
EJERCICIO 4
Encuentra una función polinomial que tiene raíces -4, -2, 2, 4.
Solución
Aquí, tenemos las raíces -4, -2, 2, 4, por lo que la función polinomial que contiene estas raíces es:
$latex f(x)=(x+4)(x+2)(x-2)(x-4)$
Entonces, el la función polinomial es $latex f(x)=(x+4)(x+2)(x-2)(x-4)$ o un múltiplo de esta función.
Siempre tenemos que recordar asignar correctamente los signos a las constantes de cada factor. Por ejemplo si es que la raíz es -4, el factor es $latex (x+4)$ y si es que la raíz es 4, el factor es $latex (x-4)$.
EJERCICIO 5
Escribe una función polinomial que tiene raíces -5, -2, 1, 5, 6.
Solución
Similar a los anteriores ejercicios, simplemente formamos factores con las raíces dadas. Entonces, tenemos:
$$f(x)=(x+5)(x+2)(x-1)(x-5)(x-6)$$
Esto significa que la función polinomial que tiene las raíces -5, -2, 1, 5, 6 es la función $$f(x)=(x+5)(x+2)(x-1)(x-5)(x-6)$$ o un múltiplo de esta función como $$f(x)=4(x+5)(x+2)(x-1)(x-5)(x-6)$$ o $$f(x)=-3(x+5)(x+2)(x-1)(x-5)(x-6)$$.
Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas
Ejercicios de funciones polinomiales para resolver
Usa los siguientes ejercicios para practicar lo aprendido sobre funciones polinomiales. Selecciona una respuesta y verifícala para saber si escogiste la correcta.
→ Explora más ejercicios de práctica
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
