Aplicaciones de las Funciones Cuadráticas

Aplicaciones importantes de las funciones cuadráticas

Existen varias aplicaciones importantes de las funciones cuadráticas en matemáticas y otros campos, que incluyen:

Física

Las funciones cuadráticas pueden ser aplicadas en física para modelar el movimiento de partículas y cuerpos rígidos bajo la influencia de fuerzas.

Por ejemplo, las ecuaciones de movimiento de un proyectil bajo la influencia de la gravedad se pueden modelar mediante una función cuadrática.

Ingeniería

Las funciones cuadráticas se utilizan para diseñar y analizar estructuras y sistemas mecánicos, como puentes y edificios. Por ejemplo, la deflexión de una viga bajo una carga se puede modelar usando una función cuadrática.

Economía

Podemos usar funciones cuadráticas para modelar la relación entre la oferta y la demanda y para analizar el equilibrio del mercado. Es decir, nos permite entender la relación entre el precio y la cantidad ofrecida y demandada en un mercado.

Optimización

Las funciones cuadráticas se utilizan en problemas de optimización, como encontrar el valor mínimo o máximo de una función.

Por ejemplo, en el aprendizaje automático, las funciones cuadráticas se utilizan en la programación lineal y cuadrática para encontrar los mejores parámetros para un modelo que minimice una función de error.

Geometría

Las funciones cuadráticas son usadas para definir y analizar parábolas, que son el conjunto de todos los puntos que son equidistantes de un punto fijo y una línea fija.

Procesamiento de señales

Las señales de audio e imagen pueden ser modeladas y procesadas usando funciones cuadráticas. Por ejemplo, en el procesamiento de señales de audio, las funciones cuadráticas se utilizan para modelar la respuesta de frecuencia de los filtros y ecualizadores de audio.

Mecánica cuántica

En la mecánica cuántica, las funciones cuadráticas se utilizan para describir el comportamiento de las propiedades ondulatorias de las partículas subatómicas.

Cálculo de áreas

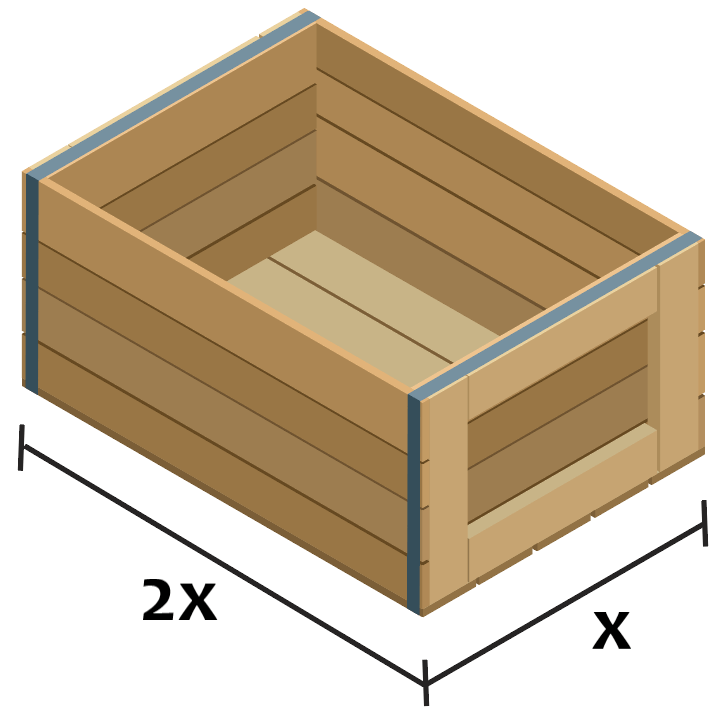
En nuestro día a día, muchas veces tenemos que encontrar el área de un departamento, el área de un lote de terreno o el área de cajas y otros objetos. Un ejemplo de esto involucra construir una caja rectangular en donde un lado debe tener el doble de la longitud del otro lado.

Por ejemplo, si es que solo tenemos 9 metros cuadrados para usar para la parte inferior de la caja, con esta información, podemos crear una ecuación para el área de la caja usando las proporciones entre ambos lados.

Esto significa que el área, la cual es igual a la longitud multiplicada por el ancho, en términos de x sería igual a x multiplicado por 2x o $latex 2{{x}^2}$. Esta ecuación debe ser igual o menor que 9 para poder construir una caja con esas restricciones.

Encontrar las ganancias

Muchas veces las funciones cuadráticas pueden ser usadas para calcular las ganancias de un negocio. Si es que queremos vender algo, incluso si es algo simple como galletas, necesitamos determinar cuántos paquetes producir de forma que podamos obtener ganancias.

Por ejemplo, si es que estamos vendiendo paquetes de galletas y queremos producir 20 paquetes, sabemos que venderemos un número diferente de paquetes dependiendo en cómo establezcamos el precio.

Si es que ponemos un precio de 100 dólares por paquete, tal vez no vendamos ningún paquete, pero si ponemos un precio de 0.01 dólares por paquete, probablemente venderemos los 20 paquetes en un minuto.

Por lo tanto, para decidir el precio que usaremos, podemos hacer que la P sea una variable. Estimamos que la demanda para los paquetes de galletas sea $latex 20-P$. Entonces, los ingresos serán iguales al precio multiplicado por el número de paquetes vendidos: $latex P(20-P)=20P-{{P}^2}$. Usando el costo de producir los paquetes de galletas, podemos hacer que nuestra ecuación sea igual a esa cantidad y de allí escoger un precio.

Funciones cuadráticas en deportes

Las funciones cuadráticas resultan muy útiles en los eventos deportivos que involucran el lanzamiento de objetos como lanzamiento de jabalina o lanzamiento de disco. Por ejemplo, supongamos que lanzas un balón al aire y quieres que tu amigo lo atrape, pero quieres darle el tiempo preciso en el que el balón llegará.

Podemos usar la ecuación de velocidad, la cual calcula la altura del balón basado en una ecuación parabólica o cuadrática. Entonces, supongamos que lanzamos el balón desde una altura de 2 metros.

También asumamos que lanzamos el balón a una velocidad de 10 metros por segundo hacia arriba y que la gravedad de la Tierra está reduciendo la velocidad del balón a un ritmo de 5 metros por segundo al cuadrado.

Con estos datos, podemos calcular la altura del balón, h, usando la variable t para el tiempo en la ecuación $latex h=2+10t-5{{t}^2}$. Si es que los brazos de tu amigo también se encuentran a 2 metros de altura, ¿cuántos segundos tomará el balón para llegar a él?. Para responder esto usamos $latex h=2$ y resolvemos para t. La respuesta es aproximadamente 2 segundos.

Calcular velocidades

Las ecuaciones y las funciones cuadráticas también son útiles para calcular velocidades. Por ejemplo, los kayakistas más experimentados usan ecuaciones cuadráticas para estimar su velocidad cuando se mueven a lo largo de un río.

Asumamos que un kayakista está viajando río arriba y el río se mueve a 3 kilómetros por hora. Si es que viaja río arriba contra la corriente por 10 km y el viaje de ida y vuelta le toma 2 horas, recordamos que $latex \text{tiempo}=\frac{\text{distancia}}{\text{velocidad}}$, en donde usamos $latex v=\text{velocidad del kayak}$ $latex \text{relativo a la tierra}$ y usamos $latex x=\text{velocidad del kayak en el agua}$.

Mientras el kayakista viaja río arriba, la velocidad del kayak es $latex v=x-3$, restamos 3 debido a la resistencia de la corriente del río, y mientras viaja río abajo, la velocidad del kayak es $latex v=x+3$. El tiempo total es igual a 2 horas, el cual es igual al tiempo empleado en viajar río arriba más el tiempo empleado en viajar río abajo y ambas distancias son 10 km.

Usando nuestras ecuaciones, sabemos que $latex 2\text{ horas}=\frac{10}{x-3}+\frac{10}{x+3}$. Una vez que expandimos esto algebraicamente, obtenemos $latex 2{{x}^2}-20x-18=0$. Al resolver para x, sabemos que el kayakista movió su kayak a una velocidad de 10.83 kilómetros por hora.

Véase también

¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:

• Gráficas de Funciones Cuadráticas
• Factorizar Polinomios de Grado 2
• Tipos de Funciones Algebraicas y sus Gráficas