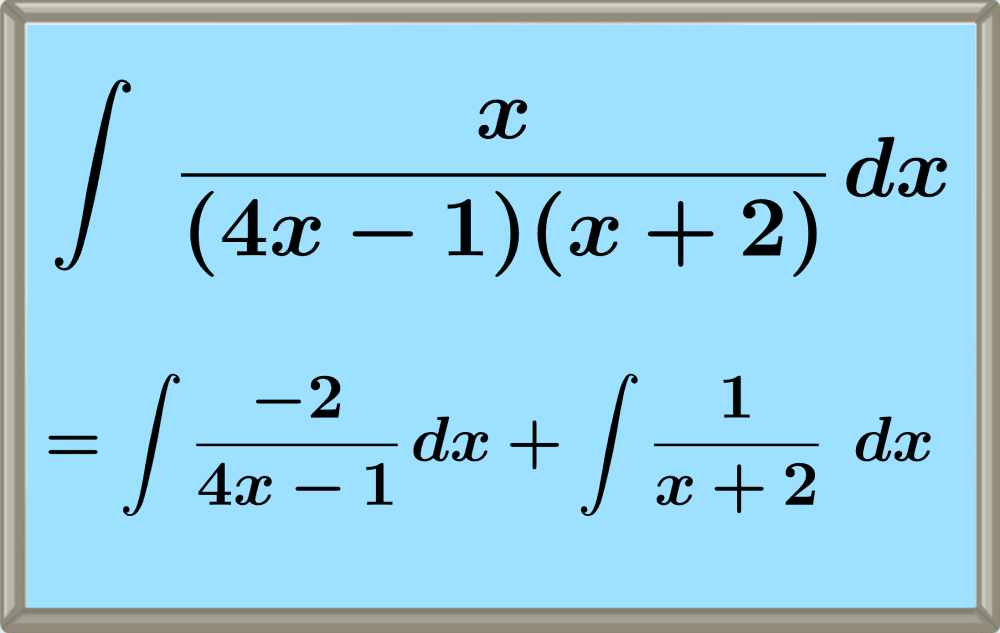Integrales por fracciones parciales – Ejercicios resueltos

Este caso corresponde a un integrando de la forma $latex \frac{P(x)}{Q(x)}$ donde el grado de $latex P(x)$ es mayor o igual que el grado de $latex Q(x)$.

En tal caso, lo primero que se debe hacer es efectuar la división de polinomios. De esta manera, el cociente $latex \frac{P(x)}{Q(x)}$ queda expresado como:

$$ \dfrac{P(x)}{Q(x)}=q(x)+\dfrac{r(x)}{Q(x)}$$

Donde $latex q(x)$ es el cociente y $latex r(x)$ el residuo. Para el integrando del ejemplo, se obtiene:

$$ (x^2+x+3)\,\div\, (x-2)= (x+3) + \dfrac{9}{x-2}$$

Con esto en mente, la integral a resolver se reescribe así:

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\int \left[(x+3) + \frac{9}{x-2}\right]dx$$

Obteniéndose tres integrales inmediatas:

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\int x\,dx+3\int dx +9\int \frac{dx}{x-2}$$

$$\int \left(\frac{x^2+x+3}{x-2}\right)dx=\frac{x^2}{2}+3x +9\ln|x-2|+C$$

Puesto que el grado del denominador es mayor que el grado del numerador, no es necesario dividir, y se pasa directamente a factorizar el denominador, lo cual es muy sencillo, ya que es una diferencia de cuadrados perfectos:

$$x^2-9=(x+3)(x-3)$$

De esta manera, la integral propuesta quedaría así:

$$\int \frac{dx}{x^2-9}=\int \frac{dx}{(x+3)(x-3)}$$

Puesto que el denominador es el producto de dos factores lineales, el integrando se puede expresar de este modo:

$$ \frac{dx}{x^2-9}=\frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

Resolviendo la suma de fracciones algebraicas, resulta:

$$ \frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

$$=\frac{A(x-3)+B(x+3)}{(x+3)(x-3)}$$

$$=\frac{Ax-3A+Bx+3B}{(x+3)(x-3)}$$

$$=\frac{x(A+B)-3A+3B}{(x+3)(x-3)}$$

Dado que el denominador siempre es el mismo, deben igualarse los numeradores:

$$x(A+B)-3A+3B = 1$$

Igualar los respectivos coeficientes de cada potencia de $latex x$, conduce a las siguientes ecuaciones:

$latex \phantom{-3}A+\phantom{3}B=0$

$latex -3A+3B=1$

Se deduce fácilmente, sumando ambas ecuaciones término a término, que:

$latex 2B=1\Rightarrow B=\dfrac{1}{2}$

Puesto que $latex A=-B$, entonces:

$latex A=-\dfrac{1}{2}$

Por lo tanto:

$$ \frac{1}{(x+3)(x-3)}=\frac{A}{x+3}+\frac{B}{x-3}$$

$$=-\frac{1}{2}\left(\frac{1}{x+3}\right)+\frac{1}{2}\left(\frac{1}{x-3}\right)$$

Y la integral buscada se transforma en:

$$\int \frac{dx}{x^2-9}=-\frac{1}{2}\int\frac{dx}{x+3}+\frac{1}{2}\int\frac{dx}{x-3}$$

$$=-\frac{1}{2}\ln\left|\frac{1}{x+3}\right|+\frac{1}{2}\ln\left|\frac{1}{x-3}\right| +C$$

Por lo tanto:

$$\int \frac{dx}{x^2-9}=-\frac{1}{2}\ln\left|\frac{1}{x+3}\right|+\frac{1}{2}\ln\left|\frac{1}{x-3}\right| +C$$

El grado del numerador es menor que el grado del denominador, por lo tanto, se factoriza este, el cual resulta ser el cubo de una suma:

$$x^3+3x^2+3x+1=(x+1)^3$$

Enseguida se escribe la integral con el denominador ya factorizado:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=\int\frac{3x+2}{(x+1)^3}dx$$

Nótese que el denominador consiste en un único factor lineal que está elevado al cubo, cuya forma es $latex (px+q)^m$, con $latex m=3$.

En tal caso, la descomposición en fracciones simples del integrando toma la siguiente forma:

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{3x+2}{(x+1)^3}=\frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{(x+1)^3}$$

Y ahora se sigue un procedimiento similar al del ejercicio anterior, con el fin de hallar los coeficientes $latex A$, $latex B$ y $latex C$:

$$\frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{(x+1)^3}=\frac{A(x+1)^2+B(x+1)+C}{(x+1)^3}$$

Seguidamente, se desarrolla el numerador cuidadosamente:

$$A(x+1)^2+B(x+1)+C =A(x^2+2x+1)+Bx+B+C$$

$$Ax^2+2Ax+A+Bx+B+C=Ax^2+(2A+B)x+B+C=3x+2$$

Al igualar los coeficientes de las potencias iguales a ambos lados de la igualdad, se obtienen las siguientes ecuaciones:

$latex A=0$

$latex 2A+B=3\Rightarrow B=3$

$latex B+C=2\Rightarrow C=-1$

Con estos valores, el integrando queda así:

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{0}{x+1}+\frac{3}{(x+1)^2}-\frac{1}{(x+1)^3}$$

$$\frac{3x+2}{x^3+3x^2+3x+1}=\frac{3}{(x+1)^2}-\frac{1}{(x+1)^3}$$

Ahora la integral original se transforma en la suma de dos integrales de fácil resolución a través de un cambio de variable sencillo:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{dx}{(x+1)^2}-\int\frac{dx}{(x+1)^3}$$

El cambio de variable es $latex u =x+1$, $latex du=dx$:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{du}{u^2}-\frac{du}{u^3}$$

Aplicando la regla de las potencias para la integración, se obtiene:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=3\int\frac{du}{u^2}-\frac{du}{u^3}$$

$$=3\int u^{-2}du-\int u^{-3}du$$

$$=\frac{3u^{-1}}{(-1)}-\frac{u^{-2}}{(-2)}+C=-\frac{3}{x+1}+\frac{1}{2(x+1)^{2}}+C$$

Finalmente:

$$\int\frac{3x+2}{x^3+3x^2+3x+1}dx=-\frac{3}{x+1}+\frac{1}{2(x+1)^{2}}+C$$

Se observa que el grado del denominador es mayor que el del numerador, por lo que se pasa a factorizar el denominador:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\int\frac{x^2+2x-1}{x(x^2+x-2)}dx$$

El trinomio $latex x^2+x-2$ se puede factorizar fácilmente:

$$x^2+x-2=(x+2)(x-1)$$

Lo cual se sustituye en el denominador del integrando:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\int\frac{x^2+2x-1}{x(x^2+x-2)}dx$$

$$=\int\frac{x^2+2x-1}{x(x+2)(x-1)}dx$$

Dado que en el denominador quedaron factores lineales, la fracción algebraica se puede expresar del siguiente modo:

$$\frac{x^2+2x-1}{x(x+2)(x-1)}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}$$

Donde los coeficientes $latex A$, $latex B$ y $latex C$ son números reales a determinar, mediante álgebra sencilla:

$$\frac{x^2+2x-1}{x(x+2)(x-1)}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}$$

$$=\frac{A(x+2)(x-1)+Bx(x-1)+Cx(x+2)}{x(x+2)(x-1)}$$

$$=\frac{A( x^2+x-2)+B(x^2-x)+C(x^2+2x)}{x(x+2)(x-1)}$$

$$=\frac{ x^2(A+B+C)+x(A-B+2C)-2A}{x(x+2)(x-1)}$$

Que da lugar a la siguiente igualdad:

$$x^2(A+B+C)+x(A-B+2C)-2A =x^2+2x-1$$

Igualando los coeficientes de las potencias semejantes, se obtienen las siguientes ecuaciones:

$latex A+B+C=1$

$latex A-B+2C=2$

$latex-2A=-1$

De esta última, se deduce fácilmente que:

$latex A = \dfrac{1}{2}$

Y sumando las dos primeras ecuaciones, $latex B$ se cancela y queda:

$latex 2A+3C=3$

Sustituyendo aquí $latex A = \dfrac{1}{2}$, resulta:

$latex 2\left(\frac{1}{2}\right)+3C=3$

$latex 1+3C=3$

$latex 3C=2$

$latex C = \dfrac{2}{3}$

Conocidos los valores de $latex A$ y $latex C$, se despeja el valor de $latex B$ de cualquiera de las ecuaciones en las que aparece:

$$A+B+C=1\Longrightarrow B=1-A-C=1-\dfrac{1}{2}-\dfrac{2}{3}=\dfrac{1}{6}$$

$latex B= -\dfrac{1}{6}$

Obtenidos los coeficientes, se sustituyen en la integral como sigue:

$$\int\frac{x^2+2x-1}{x(x+2)(x-1)}dx=\int\left[\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}\right]dx$$

$$=\int\left[\frac{1}{2x}-\frac{1}{6(x+2)}+\frac{2}{3(x-1)}\right]dx$$

$$=\int\frac{dx}{2x}-\int\frac{dx}{6(x+2)}+\int\frac{2dx}{3(x-1)}$$

$$=\frac{1}{2}\ln|x|-\frac{1}{6}\ln|x+2|+\frac{2}{3}\ln|x-1|+C$$

Entonces:

$$\int\frac{x^2+2x-1}{x^3+x^2-2x}dx=\frac{1}{2}\ln|x|-\frac{1}{6}\ln|x+2|+\frac{2}{3}\ln|x-1|+C$$

En este caso, el denominador ya está factorizado, y consiste en un factor lineal y otro cuadrático e irreducible. Cuando esto sucede, la descomposición en fracciones simples queda de esta manera:

$$\frac{2}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}$$

Siguiendo un procedimiento análogo al de los ejercicios anteriores, se efectúa la suma de fracciones:

$$\frac{A(x^2+1)+(x-1)(Bx+C)}{(x-1)(x^2+1)}=\frac{Ax^2+A+Bx^2-Bx+Cx-C}{(x-1)(x^2+1)}$$

$$=\frac{(A+B)x^2+(-B+C)x+A-C}{(x-1)(x^2+1)}=\frac{2}{(x-1)(x^2+1)}$$

Igualando los numeradores:

$$(A+B)x^2+(-B+C)x+A-C=2$$

Se obtiene el sistema de tres ecuaciones con tres incógnitas:

$latex \phantom{-}A+B=0\\-B+C=0\\\phantom{-}A-C=2\\$

Cuya solución es: $latex A=1$, $latex B=-1$, $latex C=-1$.

Así, la fracción algebraica se transforma en:

$$\frac{2}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}$$

$$\frac{1}{x-1}+\frac{(-x-1)}{x^2+1}=\frac{1}{x-1}-\frac{(x+1)}{x^2+1}$$

Y la integral queda:

$$\int\frac{2}{(x-1)(x^2+1)}dx=\int\frac{dx}{x-1}-\int\frac{xdx}{x^2+1}-\int\frac{dx}{x^2+1}\Rightarrow$$

$$\int\frac{2}{(x-1)(x^2+1)}dx=\ln\left|x-1\right|-\frac{1}{2}\ln(x^2+1)-\arctan x+C$$

En el denominador de esta integral aparece un polinomio de grado $latex 3$, que se puede factorizar mediante el método de Ruffini.

$$\begin{array}{r|rrrr}  & 1 & 0 & -2 & -4\\ 2 &  & 2 & 4 & 4\\ \hline  & 1 & 2 & 2 & 0\end{array}$$

El polinomio resultante no se puede factorizar, así que el denominador queda así:

$$x^3-2x-4 = (x-2)(x^2+2x+2)$$

De manera que el integrando se reescribe como:

$$\int\frac{3x+4}{x^3-2x-4}dx=\int\frac{3x+4}{(x-2)(x^2+2x+2)}dx$$

Puesto que el denominador consta de un factor lineal y otro factor cuadrático e irreducible, la fracción algebraica se puede descomponer de esta forma:

$$\frac{3x+4}{x^3-2x-4}=\frac{A}{(x-2)}+\frac{Bx+C}{(x^2+2x+2)}$$

$$=\frac{A(x^2+2x+2)+(Bx+C)(x-2)}{(x-2)(x^2+2x+2)}$$

$$=\frac{Ax^2+2Ax+2A+Bx^2-2Bx+Cx-2C}{(x-2)(x^2+2x+2)}$$

$$=\frac{(A+B)x^2+(2A-2B+C)x+2A-2C}{(x-2)(x^2+2x+2)}$$

Igualando los numeradores:

$$(A+B)x^2+(2A-2B+C)x+2A-2C=3x+4$$

Se obtiene el sistema de ecuaciones:

$$\phantom{2}A+\phantom{2}B\phantom{+C} = 0\\ 2A-2B+C = 3\\ 2A\phantom{-2B}-C = 4\\$$

Cuya solución es: $latex A=1$, $latex B=-1$, $latex C=-1$.

La integral propuesta se reescribe de esta forma:

$$\int\frac{3x+4}{x^3-2x-4}dx=\int\left[\frac{1}{x-2}+\frac{-x-1}{x^2+2x+2}\right]dx$$

$$=\int\frac{dx}{x-2}-\int\frac{(x+1)dx}{x^2+2x+2}$$

La primera integral es directa:

$$\int\frac{dx}{x-2}=\ln|x-2|+C$$

La segunda se resuelve fácilmente a través de un cambio de variable:

$latex u = x^2+2x+2$

$latex du = (2x+2)dx=2(x+1)dx$

$$\int\frac{(x+1)dx}{x^2+2x+2}=\int\frac{du}{2u}+C=\frac{1}{2}\ln|x^2+2x+2|+C$$

Reuniendo ambos resultados:

$$\int\frac{3x+4}{x^3-2x-4}dx=\ln|x-2|-\frac{1}{2}\ln|x^2+2x+2|+C$$

A primera vista, no parece que el método de las fracciones simples sea aplicable, sin embargo, el siguiente cambio de variable lo hace posible:

$latex u =e^t$

$latex du=e^t dt$

De esta manera, la integral se reescribe como:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\int \frac {du}{u^2+3u+2}$$

El denominador se factoriza como:

$$u^2+3u+2=(u+2)(u+1)$$

Y la integral queda expresada así:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\int \frac {du}{u^2+3u+2}=\int\frac {du}{(u+2)(u+1)}$$

De inmediato, el integrando se escribe como:

$$\frac {1}{(u+2)(u+1)}=\frac {A}{u+2}+\frac{B}{u+1}$$

$$=\frac {A(u+1)+B(u+2)}{(u+2)(u+1)}=\frac {Au+A+Bu+2B}{(u+2)(u+1)}$$

$$=\frac {u(A+B)+A+2B}{(u+2)(u+1)}$$

El sistema de ecuaciones que se obtiene al igualar los numeradores es:

$latex A+\phantom{2}B=0\\A+2B=1\\$

Cuya solución es: $latex A= -1$, $latex B =1 $.

Por lo tanto:

$$\int\frac {du}{(u+2)(u+1)}=-\int \frac{du}{x+2}+\int \frac{du}{x+1}$$

$$=-\ln|u+2|+\ln|u+1|+C$$

$$=\ln\left| \frac{u+1}{u+2}\right|+C$$

Por último, al devolver el cambio de variable hecho al comienzo, se tiene:

$$\int\frac{e^t dt}{e^{2t}+3e^t+2}=\ln\left( \frac{e^t+1}{e^t+2}\right)+C$$

Como en el caso anterior, conviene hacer el cambio de variable:

$latex u = \cos x$

$latex du=-\sin x dx$

De esta manera:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=\int\frac{-du}{u(u-1)}=-\int\frac{du}{u(u-1)}$$

El integrando se transforma en:

$$\frac{1}{u(u-1)}=\frac{A}{u}+\frac{B}{u-1}=\frac{A(u-1)+Bu}{u(u-1)}$$

$$=\frac{Au-A+Bu}{u(u-1)}=\frac{u(A+B)-A}{u(u-1)}$$

El sistema de ecuaciones resultante es:

$latex A+B=0\\\phantom{+}-A=1\\$

Luego: $latex A =-1 $, $latex B =1 $.

La integral original se transforma en:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=-\left[\int\frac{-du}{u}+\int\frac{du}{u-1}\right]$$

$$=\ln|u|-\ln|u-1|+C=\ln\left| \frac{u}{u-1}\right|+C$$

Por lo tanto:

$$\int\frac{\sin x dx}{\cos x(\cos x-1)}=\ln\left| \frac{\cos x}{\cos x-1}\right|+C$$

Como siempre, en primer lugar se halla la factorización del denominador:

$$x^4+4x^2+3=u^2+4u+3$$

Con $latex u=x^2$, en ese caso:

$$u^2+4u+3=(u+3)(u+1)=(x^2+3)(x^2+1)$$

Por lo tanto:

$$\frac{x^3+x^2+x+3}{x^4+4x^2+3}=\frac{Ax+B}{x^2+3}+\frac{Cx+D}{x^2+1}=$$

$$\frac{(Ax+B)(x^2+1)+(Cx+D)(x^2+3)}{(x^2+1)(x^2+3)}=$$

$$\frac{(Ax^3+Ax+Bx^2+B)+(Cx^3+3Cx+Dx^2+3D)}{(x^2+1)(x^2+3)}=$$

$$\frac{(A+C)x^3+(B+D)x^2+(A+3C)x+B+3D}{(x^2+1)(x^2+3)}$$

Obteniéndose las siguientes ecuaciones:

$latex A + \phantom{3}C = 1\\B +\phantom{3}D= 1\\A+3C=1\\B+3D=3\\$

Restando la tercera ecuación de arriba abajo, de la primera, se obtiene:

$latex 2C=0\Rightarrow C=0$

$latex A=1$

Y restando la cuarta de la segunda:

$latex 2D=2\Rightarrow D =1$

$latex B=0$

De esta manera:

$$\frac{x^3+x^2+x+3}{x^4+4x^2+3}=\frac{x}{x^2+3}+\frac{1}{x^2+1}$$

Y la integral se transforma en:

$$\int\frac{x^3+x^2+x+3}{x^4+4x^2+3}dx=\int\frac{x}{x^2+3}dx+\int\frac{1}{x^2+1}dx$$

Puesto que el grado del numerador es mayor que el grado del denominador, es necesario llevar a cabo previamente la división de polinomios y luego aplicar el algoritmo de la división:

$$ (x^4-6x^3+12x^2+6)\,\div\, (x^3-6x^2+12x-8)=$$

$$= x + \dfrac{8x+6}{x^3-6x^2+12x-8}$$

El denominador de la fracción algebraica es el cubo de una diferencia, por lo tanto se factoriza así:

$$x^3-6x^2+12x-8=(x-2)^3$$

Todo lo anterior conduce a:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\int xdx+\int \frac{8x+6}{x^3-6x^2+12x-8}dx=$$

$$=\int xdx+\int\frac{8x+6}{(x-2)^3}dx$$

El integrando de la segunda integral se descompone en fracciones simples de esta forma:

$$\frac{8x+6}{(x-2)^3}=\frac{A}{(x-2)}+\frac{B}{(x-2)^2}+\frac{C}{(x-2)^3}$$

Resolviendo la suma de fracciones de la derecha e igualando los numeradores, queda:

$latex A((x-2)^2+B(x-2)+C=8x+6$

$latex A(x^2-4x+4)+Bx-2B+C=8x+6$

$latex Ax^2-4Ax+4A+Bx-2B+C=8x+6$

El sistema de ecuaciones resultante es:

$$\phantom{-4}A\phantom{+B}\phantom{+C;} = 0 \\ -4A+B\phantom{+C;} = 8 \\\phantom{-}4A-2B+C = 6\\$$

Por lo tanto: $latex B = 8$

Y $latex -16+C=6\Rightarrow C =22$

Entonces:

$$\frac{8x+6}{(x-2)^3}=\frac{A}{(x-2)}+\frac{B}{(x-2)^2}+\frac{C}{(x-2)^3}$$

$$=\frac{0}{(x-2)}+\frac{8}{(x-2)^2}+\frac{22}{(x-2)^3}$$

Lo cual lleva a:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\int xdx+\int\frac{8x+6}{(x-2)^3}dx$$

$$=\int xdx+\int\frac{8}{(x-2)^2}dx+\int\frac{22}{(x-2)^3}dx$$

$$=\int xdx+8\int(x-2)^{-2}dx+22\int (x-2)^{-3}dx$$

$$=\frac{x^2}{2}-\frac{8}{x-2}-\frac{11}{(x-2)^2}+C$$

Y la respuesta es:

$$\int\frac{x^4-6x^3+12x^2+6}{x^3-6x^2+12x-8}dx=\frac{x^2}{2}-\frac{8}{x-2}-\frac{11}{(x-2)^2}+C$$