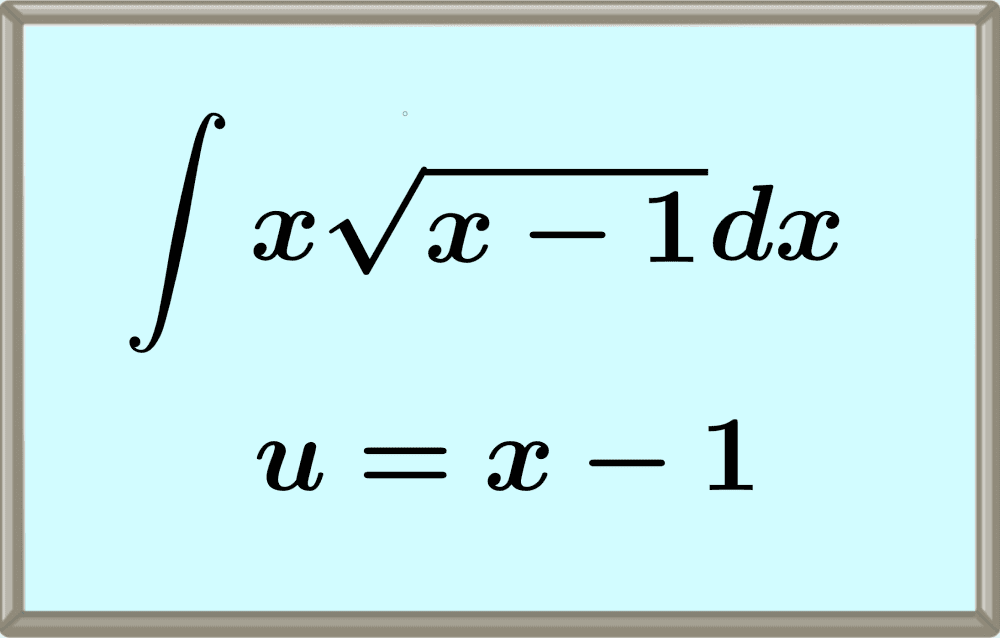Integración por sustitución – Ejercicios resueltos

El éxito de una cambio de variable consiste en hacer que la integral a resolver se transforme en una integral más simple, como por ejemplo una potencia, o la integral de alguna función elemental. En este ejemplo, se hace el siguiente cambio:

$latex u =1+2x$

$latex du =2dx$

Por lo tanto:

$latex dx =\dfrac {du}{2}$

La idea es lograr que la nueva variable y su derivada aparezcan en el integrando original. Sustituyendo los resultados anteriores y teniendo en cuenta que los coeficientes numéricos salen fuera de la integral al ser constantes, se obtiene:

$$ \int 3(1+2x)^4dx=3 \int u^4\cdot\left(\dfrac {du}{2}\right)=\frac{3}{2} \int u^4du$$

Enseguida se aplica la regla de las potencias para la integración:

$$\int kx^ndx=k\left(\dfrac{x^{n+1}}{n+1}\right)+C$$

Con $latex n \neq -1$

Además, $latex k $ es el coeficiente y $latex C$ es la constante de integración.

En este ejemplo, $latex n = 4$, por lo tanto:

$$ \int 3(1+2x)^4dx=\frac{3}{2} \int u^4du=\frac{3}{2}\left(\dfrac{u^{4+1}}{4+1}\right)+C$$

$$ \frac{3}{2} \int u^4du=\frac{3}{2}\left(\dfrac{u^5}{5}\right)+C$$

$$ \frac{3}{2} \int u^4du=\frac{3u^5}{10}+C$$

Finalmente, se devuelve el cambio realizado sustituyendo $latex u =1+2x$ en el resultado anterior:

$$ \int 3(1+2x)^4dx=\frac{3(1+2x)^5}{10}+C$$

En este tipo de integral, da buenos resultados tomar la cantidad subradical como la variable $latex u$, ya que al derivar, aparece una expresión semejante al numerador de la fracción:

$latex u =1+x^2$

$latex du =2xdx$

Al sustituir el cambio propuesto, se obtiene:

$$ \int \frac {4x}{\sqrt{1+x^2}}dx=\int \frac {2du}{\sqrt{u}}$$

Ahora se escribe el integrando como potencia:

$$\int \frac {2du}{\sqrt{u}}=2\int \left(u^{-\frac{1}{2}}\right)du$$

Aplicando la regla de las potencias con $latex n=-\dfrac{1}{2}$:

$$2\int \left(u^{-\frac{1}{2}}\right)du=2\Big[\dfrac{u^{-\frac{1}{2}+1}}{-\frac{1}{2}+1}\Big]+C=2\Big[\dfrac{u^{\frac{1}{2}}}{\frac{1}{2}}\Big]+C$$

$$2\int \left(u^{-\frac{1}{2}}\right)du=4u^{\frac{1}{2}}+C$$

Por último, se devuelve el cambio:

$$ \int \frac {4x}{\sqrt{1+x^2}}dx=4(1+x^2)^{\frac{1}{2}}+C$$

$$ \int \frac {4x}{\sqrt{1+x^2}}dx=4\sqrt{1+x^2}+C$$

Se puede hacer el siguiente cambio:

$latex u = 2x+1$

$latex du =2dx$

Con esto se obtiene:

$latex x =\dfrac{ u-1}{2}$

$latex dx =\dfrac{ du}{2}$

Ahora se transforma toda la integral a la variable $latex u$:

$$ \int \left[\dfrac{ (u-1)\sqrt{u}}{2}\right]\dfrac{ du}{2}=\frac{1}{4}\int(u-1)\sqrt{u}du$$

$$=\frac{1}{4}\int(u-1)u^\frac{1}{2}du$$

Enseguida se aplica la propiedad distributiva en el integrando:

$$ \frac{1}{4}\int(u-1)u^\frac{1}{2}du=\frac{1}{4}\int \left(u^\frac{3}{2}-u^\frac{1}{2}\right) du$$

Que conduce a dos integrales sencillas que se resuelven con la regla de las potencias:

$$ \frac{1}{4}\int \left(u^\frac{3}{2}-u^\frac{1}{2}\right) du=\frac{1}{4}\int u^\frac{3}{2}du-\frac{1}{4}\int u^\frac{1}{2}du$$

$$\frac{1}{4}\int u^\frac{3}{2}du-\frac{1}{4}\int u^\frac{1}{2}du=\frac{1}{4}\left[\dfrac{u^{\frac{3}{2}+1}}{\frac{3}{2}+1}\right]-\frac{1}{4}\left[\dfrac{u^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]+C$$

$$=\frac{1}{4}\left[\dfrac{u^{\frac{5}{2}}}{\frac{5}{2}}\right]-\frac{1}{4}\left[\dfrac{u^{\frac{3}{2}}}{\frac{3}{2}}\right]+C$$

$$=\frac{1}{10}u^{\frac{5}{2}}-\frac{1}{6}u^{\frac{3}{2}}+C$$

Ahora se regresa el resultado a la variable original:

$$ \int x\sqrt{2x+1}dx=\frac{1}{10}(2x+1)^{\frac{5}{2}}-\frac{1}{6}(2x+1)^{\frac{3}{2}}+C$$

Opcionalmente, la expresión anterior puede factorizarse:

$$ \int x\sqrt{2x+1}dx=(2x+1)^{\frac{3}{2}}\left[\left(\frac{2x+1}{10}\right)-\frac{1}{6}\right]+C$$

$$ \int x\sqrt{2x+1}dx=\sqrt{(2x+1)^3}\left(\frac{x}{5}-\frac{1}{15}\right)+C$$

$$ \int x\sqrt{2x+1}dx=\sqrt{(2x+1)^3}\left(\frac{3x-1}{15}\right)+C$$

El siguiente cambio de variable es apropiado, ya que tanto el logaritmo neperiano como su derivada aparecen en el integrando:

$latex u =5\ln x+1$

$latex du =\dfrac {5dx}{x}$

Nótese que:

$latex \dfrac {du}{5}=\dfrac {dx}{x}$

Se sustituye esto en la integral original, que conduce a:

$$ \int \frac{(5\ln x+1)^2}{x}dx=\int u^2 \left(\frac {du}{5}\right)$$

$$=\frac{1}{5}\int u^2 du$$

Aplicando la regla de las potencias:

$$ \frac{1}{5}\int u^2 du=\frac{1}{5}\left[\dfrac{u^{2+1}}{2+1}\right]+C=\dfrac{u^3}{15}+C$$

Por último, se devuelve el cambio:

$$ \int \frac{(5\ln x+1)^2}{x}dx=\dfrac{(5\ln x+1)^3}{15}+C$$

Si se toma el argumento del coseno como la variable $latex u$, su derivada está presente, veamos:

$latex u = x^4+2$

$latex du =4x^3dx$

$latex \dfrac{du}{4}=x^3dx$

Haciendo los cambios correspondientes en la integral original:

$$ \int x^3\cos(x^4+2)dx=\frac{1}{4}\int \cos u du$$

Esta es una integral inmediata que aparece en tablas:

$latex \int \cos u du= \sin u + C$

Por lo tanto:

$$\frac{1}{4}\int \cos u du=\frac{1}{4}\sin u + C$$

Devolviendo el cambio de variables:

$$ \int x^3\cos(x^4+2)dx=\frac{1}{4}\sin (x^4+2)+ C$$

El cambio de variable apropiado es:

$latex u =3x-5$

$latex du =3dx$

Sustituyendo:

$$ \int e^{3x-5}dx=\int e^u\left(\frac{du}{3}\right)$$

$$=\frac{1}{3}\int e^udu$$

Esta integral es inmediata:

$$ \frac{1}{3}\int e^udu=\frac{1}{3}e^u+C$$

Entonces:

$$ \int e^{3x-5}dx=\frac{1}{3}e^{3x-5}+C$$

Si se toma como $latex u$ el polinomio que está en el denominador, inmediatamente se observa que su derivada aparece en el numerador, lo que lleva a una integral sencilla.

En efecto:

$latex 2x^2+3x-1$

$latex du = (4x+3)dx$

Por lo tanto:

$$ \int \frac{(4x+3)dx}{2x^2+3x-1}=\int\frac{du}{u}$$

$$=ln\left | 2x^2+3x-1 \right | +C$$

Antes que nada, se reescribe la integral propuesta de la siguiente manera:

$$\int \frac {dx}{x^2+9}=\int \frac {dx}{9\left(\dfrac{x^2}{9}+1\right)}$$

Donde el 9 se saca como factor común, ahora es fácil observar que:

$$\int \frac {dx}{9\left(\dfrac{x^2}{9}+1\right)}=\frac{1}{9}\int \frac {dx}{\left[\left(\dfrac{x}{3}\right)^2+1\right]}$$

$$=\frac{1}{9}\int \dfrac {dx}{\left[1+\left(\dfrac{x}{3}\right)^2\right]}$$

El cambio de variable es el siguiente:

$latex u =\dfrac{x}{3}$

$latex du =\dfrac{dx}{3}$

$latex dx =3du$

De esta manera, la integral se transforma en:

$$\frac{1}{9}\int \dfrac {dx}{\left[1+\left(\dfrac{x}{3}\right)^2\right]}=\frac{3}{9}\int \dfrac {du}{1+u^2}$$

$$=\frac{1}{3}\int \dfrac {du}{1+u^2}$$

Esta integral aparece en las tablas:

$$\int \dfrac {dx}{1+x^2}=\arctan x + C$$

Por lo tanto:

$$\int \frac {dx}{x^2+9}=\frac{1}{3}\int \dfrac {du}{1+u^2}$$

$$=\left(\frac{1}{3}\right)\arctan u + C$$

Y al devolver el cambio, queda:

$$\int \frac {dx}{x^2+9}=\left(\frac{1}{3}\right)\arctan u + C$$

$$=\left(\frac{1}{3}\right)\arctan\left( \dfrac{x}{3} \right)+ C$$

En general, las integrales de la forma $latex \int \frac {dx}{a^2+x^2}$, se resuelven mediante:

$$\int \frac {dx}{a^2+x^2}=\frac{1}{a}\arctan\left( \dfrac{x}{a} \right)+ C$$

Inspirados en el ejemplo anterior, se reescribe la integral como:

$$\int \frac {dx}{4-x^2}=\int \frac {dx}{4\left(1-\dfrac{x^2}{4}\right)}=\frac{1}{4}\int \frac {dx}{\left[1-\left(\dfrac{x}{2}\right)^2\right]}$$

Esta vez, el cambio de variable sería:

$latex u =\dfrac{x}{2}$

$latex du =\dfrac{dx}{2}$

$latex dx =2du$

Y la integral se transforma en:

$$\int \frac {dx}{4-x^2}=\frac{2}{4}\int \frac {du}{1-u^2}=\frac{1}{2}\int \frac {du}{1-u^2}$$

Esta integral también aparece en las tablas como:

$$\int \dfrac {dx}{1-x^2}=\frac{1}{2}\ln\left |\dfrac{1+x}{1-x}\right | + C$$

De modo que solo resta sustituir:

$$\int \frac {dx}{4-x^2}=\frac{1}{2}\int \frac {du}{1-u^2}=\frac{1}{2}\cdot\frac{1}{2}\ln\left |\dfrac{1+u}{1-u}\right | + C$$

Finalmente, se regresa a la variable original:

$$\int \frac {dx}{4-x^2}=\frac{1}{4}\ln\left |\dfrac{1+\frac{x}{2}}{1-\frac{x}{2}}\right | + C=\frac{1}{4}\ln\left |\dfrac{2+x}{2-x}\right | + C$$

En general, las integrales de la forma $latex \int \frac {dx}{a^2-x^2}$, se resuelven mediante:

$$\int \frac {dx}{a^2-x^2}=\frac{1}{2a}\ln\left |\dfrac{a+x}{a-x}\right | + C$$

Alternativa, por propiedades de logaritmo:

$$\int \frac {dx}{x^2-a^2}=\frac{1}{2a}\ln\left |\dfrac{x-2}{x+a}\right | + C$$

A primera vista, esta integral no se parece mucho a las anteriores, a causa del término $latex 6x$, sin embargo, mediante el procedimiento de completar el cuadrado en el denominador, se puede obtener una integral como las de los ejemplos 8 o 9:

$$\int \frac {dx}{x^2+6x+5}=\int \frac {dx}{(x^2+2\cdot 3x+9)-9+5}$$

Nótese que con esta maniobra algebraica, el denominador no se altera, pero sí puede reescribirse de una manera completamente equivalente, así:

$$\int \frac {dx}{x^2+6x+5}=\int \frac {dx}{(x+3)^2-4}$$

Haciendo:

$latex u=x+3$

$latex du=dx$

$latex a=2$

La integral propuesta queda como la última variante del ejercicio anterior, en cuyo caso:

$$\int \frac {dx}{x^2+6x+5}=\int \frac {dx}{(x+3)^2-4}$$

$$=\int \frac {du}{u^2-4}=\frac{1}{2}\ln\left |\dfrac{u-2}{u+2}\right | + C$$

Y es muy simple devolver el cambio y obtener:

$$\int \frac {dx}{x^2+6x+5}=\frac{1}{2}\ln\left |\dfrac{(x+3)-2}{(x+3)+2}\right | + C$$

$$\int \frac {dx}{x^2+6x+5}=\frac{1}{2}\ln\left |\dfrac{x+1}{x+5}\right | + C$$