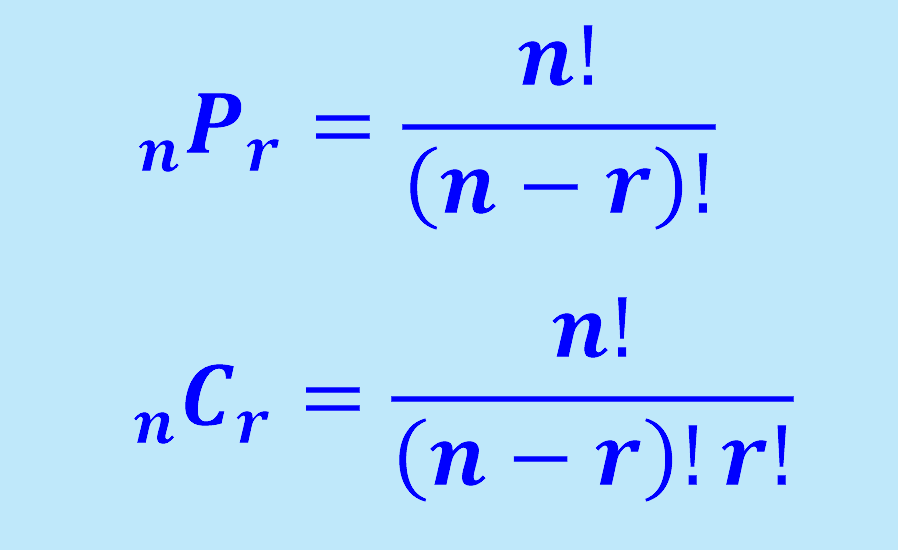La diferencia entre permutación y combinación es que, para las permutaciones, el orden de los elementos sí es tomado en consideración y para las combinaciones, el orden de los elementos no importa. Por ejemplo, la organización de objetos es un ejemplo de permutaciones, pero la selección de un grupo de objetos es un ejemplo de combinaciones.
ÁLGEBRA
Relevante para…
Conocer la diferencia entre permutación y combinación con ejemplos.
ÁLGEBRA
Relevante para…
Conocer la diferencia entre permutación y combinación con ejemplos.
Definiciones de permutaciones y combinaciones
Permutaciones
Una permutación puede ser definida como la acción de organizar a unos pocos o a todos los miembros de un conjunto en un orden específico. El proceso de ordenar elementos desordenados se llama permutación.
Combinaciones
Una combinación es el proceso de seleccionar los elementos u objetos de un conjunto en una forma que, a diferencia de las permutaciones, el orden no importa. Esto se refiere a la combinación de elementos tomados de un conjunto sin ninguna repetición.
¿Cuál es la diferencia entre permutación y combinación?
En la siguiente tabla podemos comparar a las permutaciones y las combinaciones y podemos observar sus diferencias:
| Permutaciones | Combinaciones |
| Las permutaciones son las diferentes maneras de organizar un conjunto de objetos en un orden secuencial. | Las combinaciones son varias maneras de escoger elementos de un conjunto más grande de objetos sin considerar el orden |
| El orden sí es importante. | El orden no es importante. |
| Se refiere a la organización de objetos. | No denota la organización de objetos. |
| Múltiples permutaciones pueden ser derivadas de una sola combinación. | De una permutación, sólo una combinación puede ser derivada. |
| Pueden ser definidas como elementos ordenados. | Pueden ser definidas como conjuntos sin orden. |
Ejemplos
EJEMPLO
Supongamos que tenemos que encontrar el número total de muestras probables de dos objetos de un conjunto de tres objetos A, B, C. Antes que nada, tenemos que determinar si esto es un problema de permutaciones o un problema de combinaciones. Para esto, lo único que tenemos que hacer es averiguar si es que el orden es relevante o no.
Si es que el orden es importante, entonces tenemos un problema de permutaciones. En este caso, el número posible de muestras será AB, BA, BC, CB, AC, CA. Cuando tenemos permutaciones, consideramos a AB y BA como diferentes. De igual forma, BC y CB, AC y CA son diferentes.
Si es que el orden no es importante, entonces tenemos un problema de combinaciones. En este caso, las muestras posibles son AB, BC y AC.
Preguntas frecuentes
¿Qué son las permutaciones y las combinaciones?
Una permutación es considerada como un método para organizar un conjunto de elementos en orden. Una combinación es considerada como la selección de un conjunto de elementos.
¿Cuáles son las fórmulas para las combinaciones y las permutaciones?
La fórmula para las permutaciones es $latex _{n}{{P}_{r}}=\frac{{n!}}{{({n-r})!}}$.
La fórmula para las combinaciones es $latex _{n}{{C}_{r}}=\frac{{n!}}{{( {n-r})!r!}}$.
¿Cuál es un ejemplo de permutaciones?
La organización de números, letras u otros objetos son ejemplos de permutaciones.
¿Cuál es un ejemplo de combinaciones?
La selección de objetos de una lista, seleccionar personas de un grupo son ejemplos de combinaciones.
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas: