La función y=ex es llamada la función exponencial. La derivada de la función exponencial ex es igual a ex. Esto también significa que la integral de ex es ex. Funciones exponenciales compuestas pueden ser derivadas con la regla de la cadena.
A continuación, conoceremos por qué la derivada de ex es ex. Además, aprenderemos a resolver funciones exponenciales compuestas con algunos ejercicios.
CÁLCULO
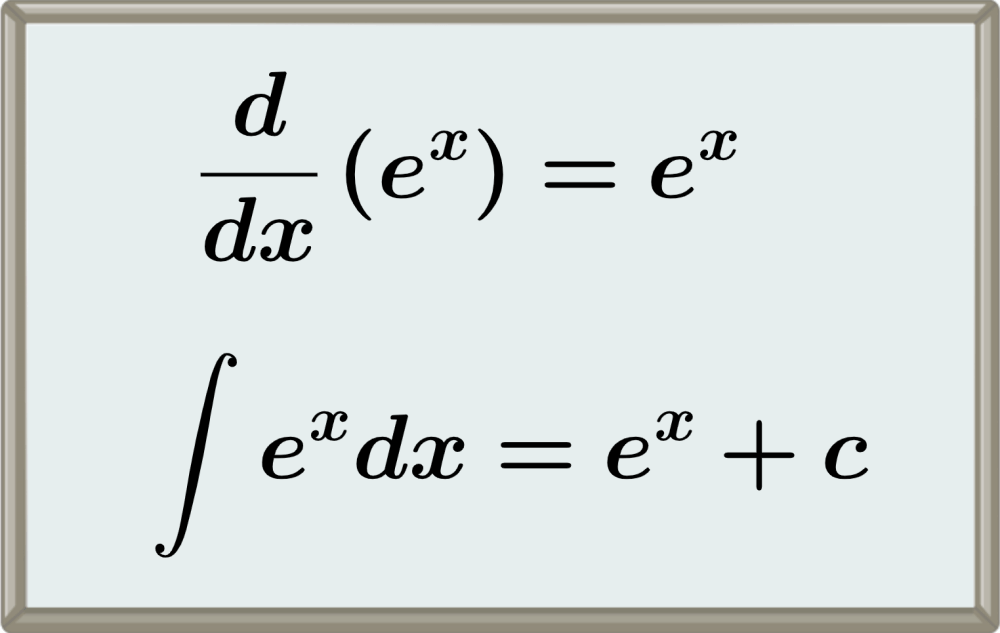
Relevante para…
Aprender sobre derivadas e integrales de funciones exponenciales.
CÁLCULO
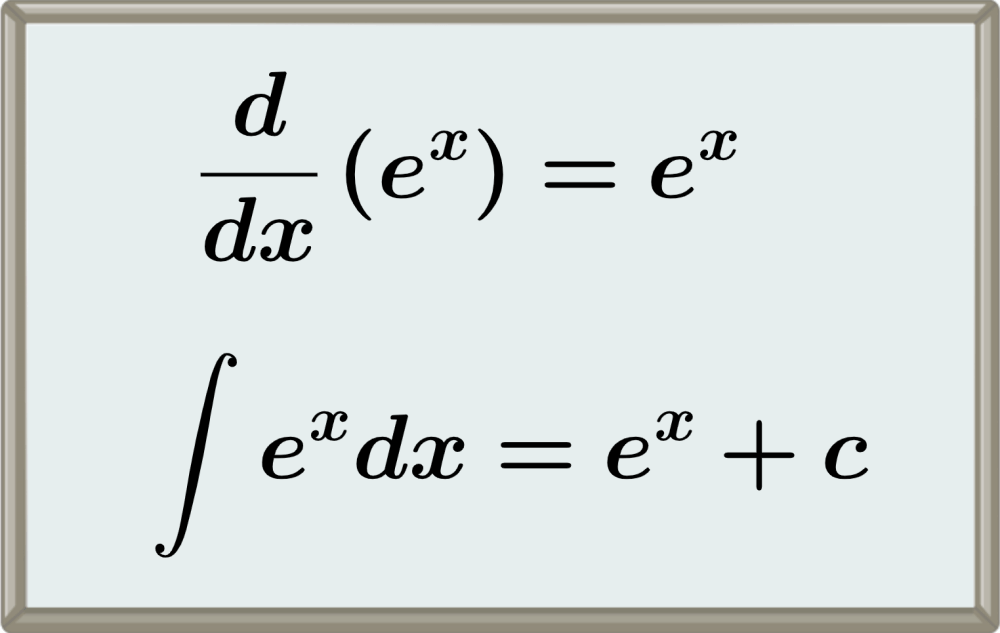
Relevante para…
Aprender sobre derivadas e integrales de funciones exponenciales.
¿Por qué la derivada de ex es ex?
La derivada de la función exponencial ex es ex porque la pendiente de la curva ex es igual a ex.
Podemos visualizar esta idea al considerar a la gráfica de la función $latex y=2^x$ que se muestra a continuación:
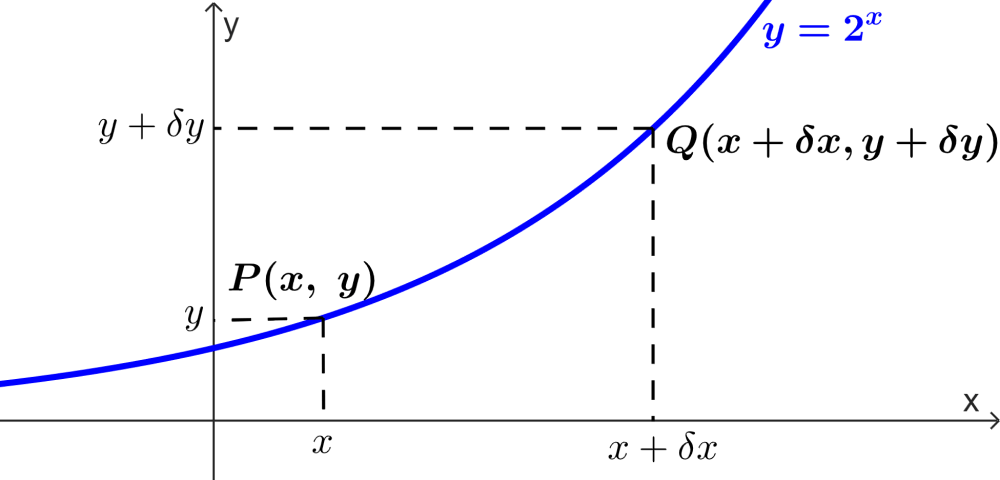
Los puntos $latex P(x,~y)$ y $latex Q(x+\delta x,~y+\delta y)$ son dos puntos cercamos que se ubican en la curva $latex y=2^x$. Entonces, tenemos:
$latex y+\delta y=2^{x+\delta x}$
$latex \delta y=2^{x+\delta x}-y$
$latex =2^{x+\delta x}-2^x$
$latex \delta y=2^x(2^{\delta x}-1)$
Si es que dividimos ambos lados de esta ecuación por $latex \delta x$, tenemos:
$$\frac{\delta y}{\delta x}=2^x\left(\frac{2^{\delta x}-1}{\delta x}\right)$$
Considerando que $latex \frac{dy}{dx}=\lim_{\delta x \to 0}\left[\frac{\delta y}{\delta x}\right]$, tenemos:
$$\frac{dy}{dx}=\lim_{\delta x \to 0}\left[ 2^x\left(\frac{2^{\delta x}-1}{\delta x}\right)\right]$$
$$=2^x \times \lim_{\delta x \to 0}\left(\frac{2^{\delta x}-1}{\delta x}\right)$$
Tomando valores muy pequeños de $latex \delta x$ y usando una calculadora, tenemos:
$$\lim_{\delta x \to 0}\left(\frac{2^{\delta x}-1}{\delta x}\right)\approx 0.693$$
Esto significa que la derivada de $latex 2^x$ es:
$$\dfrac{d}{dx}(2^x)\approx 0.693 \times 2^x$$
Si es que realizamos lo mismo para $latex 3^x$, tenemos:
$$\frac{d}{dx}(3^x)=3^x \times \lim_{\delta x \to 0}\left(\frac{3^{\delta x}-1}{\delta x}\right)$$
Tomando valores muy pequeños de $latex \delta x$ y usando una calculadora, tenemos:
$$\lim_{\delta x \to 0}\left(\frac{3^{\delta x}-1}{\delta x}\right)\approx 1.099$$
$$\dfrac{d}{dx}(3^x)\approx 1.099 \times 3^x$$
Podemos observar que para $latex y=2^x$, la pendiente de la curva ($latex \frac{dy}{dx}$) es menos de $latex y=2^x$ y en el caso de $latex y=3^x$, la pendiente es mayor que $latex y=3^x$.
Existe una función exponencial $latex y=a^x$ en la que su pendiente es igual a $latex y=a^x$. Este valor es $latex a=2.71828$ y es denotado por el símbolo $latex e$.
Ejercicios resueltos de derivadas e integrales de funciones exponenciales
EJERCICIO 1
Encuentra la derivada de la función $latex y=e^{3x}$.
Solución
Sabemos que la derivada de la función $latex y=e^x$ es $latex \frac{dy}{dx}=e^x$.
Entonces, usamos la regla de la cadena para derivar:
$$\frac{dy}{dx}=e^{2x}(2x)^{\prime}$$
$$\frac{dy}{dx}=2 e^{2x}$$
EJERCICIO 2
¿Cuál es la derivada de la función $latex y=5e^{\frac{1}{x}}$?
Solución
Usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=5e^{\frac{1}{x}}\left(\frac{1}{x}\right)^{\prime}$$
$$=5e^{\frac{1}{x}}\left(-\frac{1}{x^2}\right)$$
$$\frac{dy}{dx}=-\frac{5}{x^2}e^{\frac{1}{x}}$$
EJERCICIO 3
Encuentra la derivada de la siguiente función:
$$y=\frac{2}{3+e^{3x}}$$
Solución
Podemos escribir a la función de la siguiente forma:
$latex y=2(3+e^{3x})^{-1}$
Ahora, usamos la regla de la cadena:
$$\dfrac{dy}{dx}=-2(3+e^{3x})^{-2}(3+e^{3x})^{\prime}$$
$$=-2(3+e^{3x})^{-2}(3e^{3x})$$
$$\dfrac{dy}{dx}=\frac{-6e^{3x}}{(3+e^{3x})^2}$$
EJERCICIO 4
Resuelve la siguiente integral:
$$\int 2e^{-x} dx$$
Solución
Para resolver esta integral, observamos que la derivada de $latex e^{-x}$ es $latex -e^{-x}$. Entonces, tenemos:
$$\int 2e^{-x} dx =-2e^{-x}+c$$
EJERCICIO 5
Encuentra el resultado de la siguiente integral:
$$\int (1-e^{-3x})^2 dx$$
Solución
Podemos empezar por expandir la expresión del paréntesis para obtener:
$$\int (1-e^{-3x})^2 dx = \int (1-2e^{-3x}+e^{-6x}) dx$$
Entonces, tenemos:
$$\int (1-e^{-3x})^2 dx = x+\frac{2}{3}e^{-3x}-\frac{e^{-6x}}{6}+c$$
EJERCICIO 6
Encuentra la derivada de la siguiente función:
$latex y=x^2e^x$
Solución
En este caso, podemos usar la regla del producto de derivadas y tenemos:
$$\dfrac{dy}{dx}=x^2(e^x)^{\prime}+e^x(x^2)^{\prime}$$
$$=x^2e^x+2xe^x$$
$$\dfrac{dy}{dx}=xe^x(x+2)$$
Derivadas e integrales de funciones exponenciales – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre derivadas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
