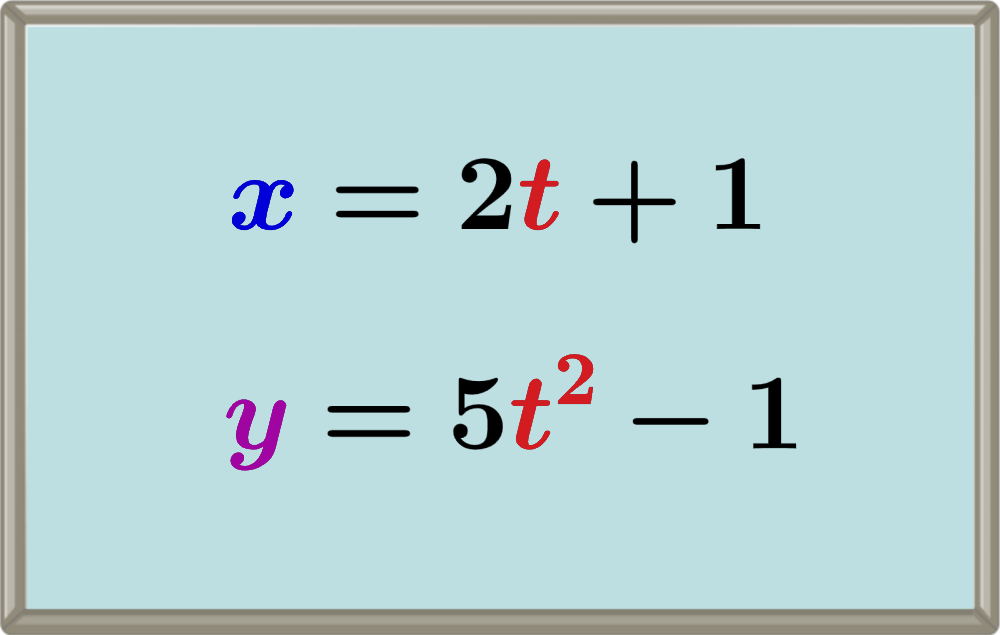Las derivadas de ecuaciones paramétricas son encontradas al derivar a cada ecuación con respecto a t. Luego, la regla de la cadena es usada para obtener una derivada de y con respecto a x.
A continuación, conoceremos cómo encontrar las derivadas de ecuaciones paramétricas. Usaremos varios ejemplos y ejercicios prácticos.
Diferenciación de ecuaciones paramétricas
Vamos a aprender cómo encontrar las derivadas de ecuaciones paramétricas usando un ejemplo.
Consideremos a las siguientes ecuaciones paramétricas:
$latex x=t+1~~$ $latex ~~y=t^2$
Cuando derivamos a $latex x$ con respecto a $latex t$ y cuando derivamos a $latex y $ con respecto a $latex t$, tenemos:
$latex \dfrac{dx}{dt}=1~~$ $latex ~~\dfrac{dy}{dt}=2t$
Usando la regla de la cadena, podemos escribir de la siguiente forma:
$$\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$$
Entonces, tenemos:
$$\frac{dy}{dx}=2t(1)=2t$$
Dado que tenemos $latex x=t+1$, podemos escribir $latex t=x-1$ y la derivada es:
$$\frac{dy}{dx}=2t$$
$$\frac{dy}{dx}=2x-2$$
Ejercicios resueltos de derivadas paramétricas
EJERCICIO 1
Encuentra $latex \dfrac{dy}{dx}$ en términos del parámetro $latex t$ para:
$latex y=3t^2+2t$
$latex x=1-2t$
Solución
Empezamos encontrando las derivadas $latex \frac{dy}{dt}$ y $latex \frac{dx}{dt}$:
- Cuando $latex y=3t^2+2t$, tenemos: $latex \dfrac{dy}{dt}=6t+2$
- Cuando $latex x=1-2t$, tenemos: $latex \dfrac{dx}{dt}=-2$
Usando la regla de la cadena, podemos escribir lo siguiente:
$$ \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$$
$$=(6t+2)\left(-\frac{1}{2}\right)$$
$$ \frac{dy}{dx}=-3t-1$$
EJERCICIO 2
¿Cuál es la derivada $latex \dfrac{dy}{dx}$ de las siguientes ecuaciones? Escríbela en términos del parámetro $latex t$.
$latex y=(1+2t)^3$
$latex x=t^3$
Solución
Vamos a encontrar las derivadas $latex \frac{dy}{dt}$ y $latex \frac{dx}{dt}$:
- Cuando $latex y=(1+2t)^3$, tenemos: $latex \dfrac{dy}{dt}=3(1+2t)^2(2)$. Entonces, tenemos: $latex \dfrac{dy}{dt}=6(1+2t)^2$
- Cuando $latex x=t^3$, tenemos: $latex \dfrac{dx}{dt}=3t^2$
Con la regla de la cadena, tenemos:
$$ \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$$
$$=6(1+2t)^2\times \frac{1}{3t^2}$$
$$ \frac{dy}{dx}=\frac{2(1+2t)^2}{t^2}$$
EJERCICIO 3
Encuentra $latex \dfrac{dy}{dx}$ en términos de $latex t$ de las siguientes ecuaciones:
$latex x=3t^4$
$latex y=2t^2-3$
Solución
Tenemos que encontrar las derivadas $latex \frac{dy}{dt}$ y $latex \frac{dx}{dt}$:
- Cuando $latex y=2t^2-3$, tenemos: $latex \dfrac{dy}{dt}=4t$
- Cuando $latex x=3t^4$, tenemos: $latex \dfrac{dx}{dt}=12t^3$
Ahora, podemos usar la regla de la cadena para encontrar $latex \dfrac{dy}{dx}$:
$$ \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$$
$$=4t\times \frac{1}{12t^3}$$
$$ \frac{dy}{dx}=\frac{1}{3t^2}$$
EJERCICIO 4
¿Cuál es la derivada $latex \dfrac{dy}{dx}$ de las siguientes ecuaciones? Escríbela en términos de $latex t$.
$latex x=2\sqrt{t}$
$latex y=5t-4$
Solución
Empezamos por encontrar las derivadas $latex \frac{dy}{dt}$ y $latex \frac{dx}{dt}$:
- Cuando $latex y=5t-4$, tenemos: $latex \dfrac{dy}{dt}=5$
- Cuando $latex x=2\sqrt{t}=2t^{\frac{1}{2}}$, tenemos: $latex \dfrac{dx}{dt}=t^{-\frac{1}{2}}$
Ahora, encontramos $latex \dfrac{dy}{dx}$ usando la regla de la cadena:
$$ \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$$
$$=5\times \frac{1}{t^{-\frac{1}{2}}}$$
$$ \frac{dy}{dx}=5\sqrt{t}$$
EJERCICIO 5
Encuentra la ecuación de la recta tangente a la curva dada paramétricamente por $latex x=\frac{2}{t}$ y $latex y=3t^2-1$ en el punto (2, 2).
Solución
Podemos encontrar el valor del parámetro $latex t$ sustituyendo $latex x=2$, $latex y=2$ en las ecuaciones
$latex x=\dfrac{2}{t}~~$ $latex ~~y=3t^2-1$
Esto nos da $latex t=1$.
Al diferenciar paramétricamente, tenemos:
$latex \dfrac{dy}{dt}=6t~~$ $latex ~~\dfrac{dx}{dt}=-\dfrac{2}{t^2}$
Cuando $latex t=1$, tenemos:
$$\frac{dy}{dx}\Big|_{t=1}=-3$$
Esto significa que la pendiente de la recta tangente es -3. Entonces, la ecuación de la tangente tiene la forma
$latex y=-3x+c$
Como la recta tangente pasa por el punto (2, 2), tenemos:
$latex 2=-3(2)+c$
$latex c=8$
La ecuación de la recta tangente es $latex y=-3x+8$.
EJERCICIO 6
Encuentra la segunda derivada $latex \dfrac{d^2y}{dx^2}$ en términos de $latex t$ de las siguientes ecuaciones paramétricas:
$latex x=t+1$
$latex y=t^3$
Solución
Derivando a cada ecuación con respecto a $latex t$, tenemos:
$latex \dfrac{dy}{dt}=1~~$ $latex ~~\dfrac{dy}{dt}=3t^2$
Usando la regla de la cadena, tenemos
$$\frac{dy}{dx}=\frac{dy}{dt} \frac{dt}{dx}=3t^2$$
Ahora, derivamos a cada término de esta ecuación con respecto a $latex x$ para encontrar la segunda derivada $latex \dfrac{d^2y}{dx^2}$:
$$\frac{d}{dx}\left( \frac{dy}{dx}\right)=\frac{d}{dx}(3t^2)$$
Dado que no podemos derivar a $latex 3t^2$ con respecto a $latex x$, usamos la regla de la cadena:
$$\frac{d}{dx}(3t^2)=\frac{d}{dt}(3t^2) \frac{dt}{dx}$$
$$=6t \frac{dt}{dx}$$
Sustituyendo esto, tenemos:
$$\frac{d^2y}{dx^2}=6t \frac{dt}{dx}$$
Dado que $latex \frac{dx}{dt}=1$, podemos escribir:
$$\frac{dx}{dt}=\frac{1}{\frac{dx}{dt}}=1$$
Entonces, la segunda derivada es:
$$\frac{d^2y}{dx^2}=6t (1)=6t$$
Derivadas paramétricas – Ejercicios para resolver
La derivada $latex \frac{dy}{dx}$ en términos de t de las ecuaciones $latex x=4t(t-2)$ y $latex y=(t-1)^3$ es una fracción. ¿Cuál es el numerador?
Escribe el numerador en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
