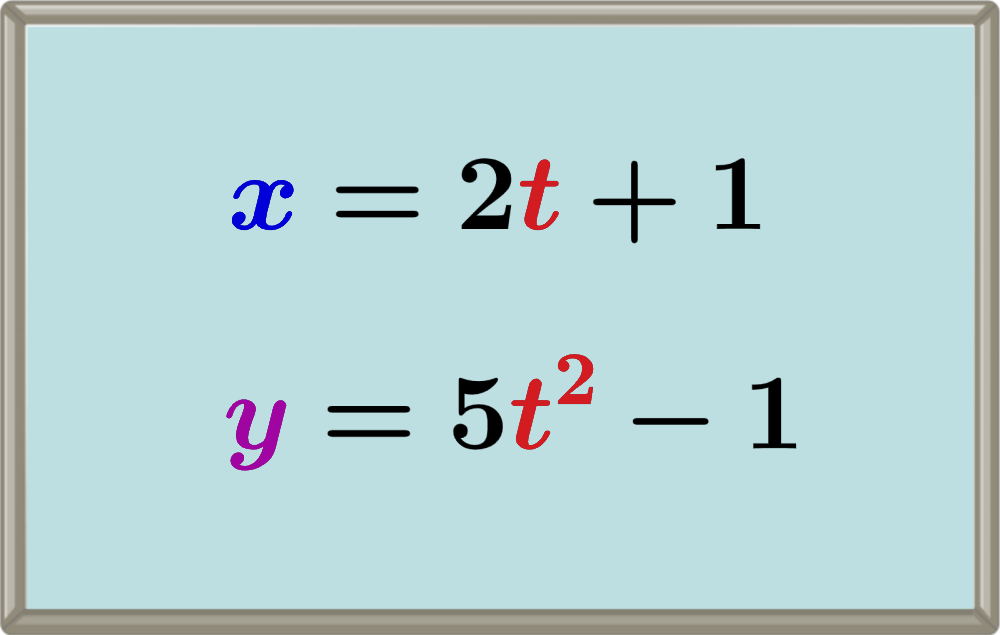Las ecuaciones paramétricas son ecuaciones en las que y es una función de x, pero tanto x como y están definidas en términos de una tercera variable. La tercera variable es el parámetro de las ecuaciones. Frecuentemente, la variable t es usada en este tipo de ecuaciones.
A continuación, aprenderemos sobre las ecuaciones paramétricas con ejercicios resueltos. Además, veremos algunos ejercicios para resolver.
Resumen de ecuaciones paramétricas
En las ecuaciones paramétricas, $latex y$ es definido como una función de $latex x$ al expresar tanto a $latex y$ como a $latex x$ en términos de una tercera variable conocida como un parámetro.
Por ejemplo, las siguientes ecuaciones son ecuaciones paramétricas en donde el parámetro es $latex t$.
$latex x=t+1~~~[1]$
$latex y=t^2~~~[2]$
Estas ecuaciones paramétricas definen a la parábola con la ecuación:
$latex y=x^2-2x+1$
Podemos obtener esto al eliminar el parámetro $latex t$ en las ecuaciones [1] y [2]. Si es que resolvemos la ecuación [1] para $latex t$, tenemos $latex t=x-1$. Sustituyendo esto en la ecuación [2], tenemos:
$latex y=(x-1)^2$
$latex y=x^2-2x+1$
Ejercicios resueltos de ecuaciones paramétricas
EJERCICIO 1
¿Cuál es la ecuación cartesiana de las siguientes ecuaciones paramétricas?
$latex x=\sqrt{t}$
$latex y=3t^2-4$
Solución
Una ecuación cartesiana es una ecuación de y expresada en términos de x. Entonces, tenemos que eliminar el parámetro $latex t$.
Empezamos resolviendo la primera ecuación para $latex t$. Para esto elevamos ambos lados al cuadrado:
$latex x=\sqrt{t}$
$latex x^2=t$
Sustituyendo esta expresión en la segunda ecuación, tenemos:
$latex y=3t^2-4$
$latex y=3(x^2)^2-4$
$latex y=3x^4-4$
EJERCICIO 2
Encuentra la ecuación cartesiana para las siguientes ecuaciones paramétricas:
$latex x=2t-1$
$latex y=12t^2-5$
Solución
Para obtener una ecuación cartesiana, tenemos que obtener una ecuación de y en términos de x.
Entonces, empezamos resolviendo la primera ecuación para $latex t$:
$latex x=2t-1$
$$t=\frac{x+1}{2}$$
Ahora, sustituimos esta expresión en la segunda ecuación:
$latex y=12t^2-5$
$$y=12\left(\frac{x+1}{2}\right)^2-5$$
$$y=12\left(\frac{x^2+2x+1}{4}\right)-5$$
$$y=3x^2+6x+3-5$$
$latex y=3x^2+6x-2$
EJERCICIO 3
Expresa a y como una ecuación de x usando las siguientes ecuaciones paramétricas:
$latex x=2\sqrt{t}$
$latex y=8t^2+5$
Solución
Para expresar a $latex y$ como una ecuación de $latex x$, tenemos que empezar resolviendo la primera ecuación para $latex t$:
$latex x=2\sqrt{t}$
$$\sqrt{t}=\frac{x}{2}$$
$latex t=\frac{x^2}{4}$
Ahora, usamos esta expresión en la segunda ecuación:
$latex y=8t^2+5$
$$y=8\left(\frac{x^2}{4}\right)^2+5$$
$$y=8\left(\frac{x^4}{16}\right)+5$$
$$y=\frac{x^4}{2}+5$$
EJERCICIO 4
Encuentra la ecuación cartesiana para las siguientes ecuaciones paramétricas:
$$x=\frac{1}{t}$$
$latex y=3t-2$
Solución
Resolviendo la primera ecuación para $latex t$, tenemos:
$$x=\frac{1}{t}$$
$$t=\frac{1}{x}$$
Sustituyendo esta expresión en la segunda ecuación, tenemos:
$latex y=3t-2$
$$y=3\left(\frac{1}{x}\right)-2$$
$$y=\frac{3}{x}-2$$
Podemos multiplicar a toda la ecuación por $latex x$ para obtener $latex xy+2x=3$.
EJERCICIO 5
Encuentra una ecuación para y en términos de x usando las siguientes ecuaciones:
$$x=\frac{2}{\sqrt{x}}$$
$$y=\frac{3}{1+3}$$
Solución
Empezamos encontrando una expresión para $latex t$ en términos de $latex x$:
$$x=\frac{2}{\sqrt{t}}$$
$$x^2=\frac{4}{t}$$
$$t=\frac{4}{x^2}$$
Ahora, usamos esta expresión en la segunda ecuación:
$$y=\frac{3}{1+t}$$
$$y=\frac{3}{1+\frac{4}{x^2}}$$
Para simplificar, podemos multiplicar tanto al numerador, como al denominador por $latex x^2$:
$$y=\frac{3x^2}{x^2+4}$$
EJERCICIO 6
Encuentra una ecuación cartesiana usando las siguientes ecuaciones paramétricas:
$$x=\frac{1}{2-t}$$
$$y=\frac{3}{1+2t}$$
Solución
La ecuación de $latex x$ puede ser resuelta para $latex t$ de la siguiente forma:
$$x=\frac{1}{2-t}$$
$latex x(x-t)=1$
$latex 2x-xt=1$
$latex xt=2x-1$
$$t=\frac{2x-1}{x}$$
Sustituyendo esta expresión en la ecuación de $latex y$, tenemos:
$$y=\frac{3}{1+2t}$$
$$y=\frac{3}{1+2\left(\frac{2x-1}{x}\right)}$$
$$y=\frac{3x}{x+2(2x-1)}$$
$$y=\frac{3x}{5x-2}$$
Ecuaciones paramétricas – Ejercicios para resolver
La ecuación cartesiana de las ecuaciones $latex x=\frac{t}{1-3t}$, $latex y=\frac{t}{1+2t}$ es escrita como una fracción. ¿Cuál es el denominador?
Escribe el denominador en la casilla.
Véase también
¿Interesado en aprender más sobre ecuaciones paramétricas y cálculo? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
