Para que una relación sea una función, podemos tener dos casos. El primero sucede cuando la relación es uno a uno y el segundo caso sucede cuando la relación es muchos a uno. Esencialmente, esto significa que una función puede tener varios valores de entrada que produzcan el mismo valor de salida, pero no varias salidas producidas por una sola entrada.
A continuación, aprenderemos sobre los dos casos de relaciones que sí son consideradas funciones. Además, veremos algunos ejemplos para aplicar los conceptos.
Caso (i): Relación uno a uno
Vamos a considerar a dos conjuntos no vacíos A y B. Una relación de A a B es una regla que asocia a cada elemento del conjunto A con un elemento del conjunto B.
Una relación puede ser representada usando un diagrama de mapeo. Consideremos a la siguiente relación que tiene los conjuntos A={-2, -1, 0, 1, 2} y B={0, 1, 2, 3, 4, 5, 6}.
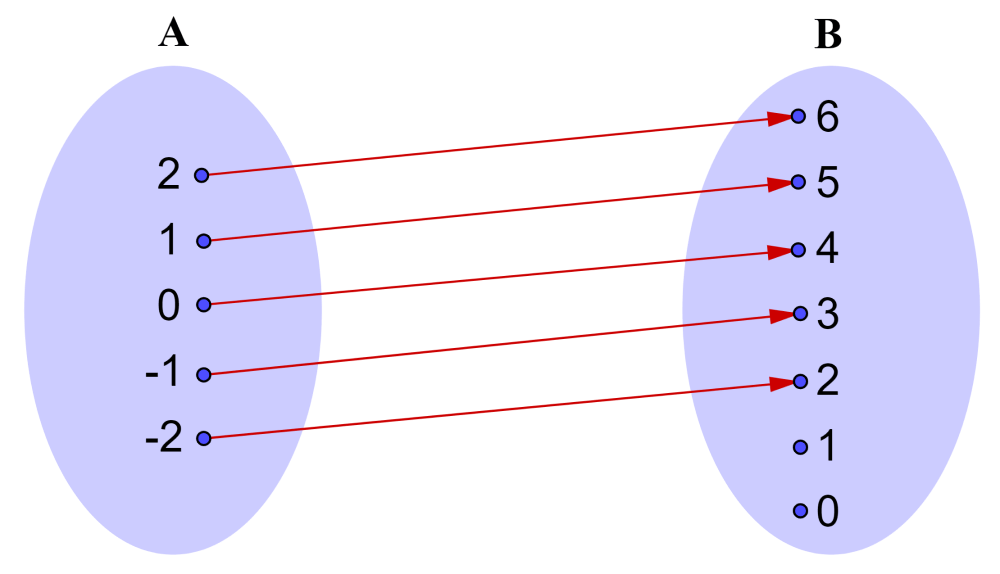
En el caso (i), observamos que cada elemento del conjunto A se relaciona únicamente con un elemento del conjunto B. Esta es una relación llamada uno a uno.
El hecho que no haya elementos del conjunto A que se relacionen con los elementos 0 o 1 en el conjunto B no es importante.
Una relación uno a uno es llamada una función. Usualmente, denotamos usando a f a la regla que asocia a cada elemento de A a un elemento de B.
Por ejemplo, en la relación que tenemos arriba, la regla es «sumar 4». Usando la notación de funciones, podemos escribir:
$latex f(x)=x+4~~$ o $latex ~~f:~x\rightarrow x+4$
Caso (ii): Relación muchos a uno
Nuevamente, vamos a considerar a los conjuntos A={-2, -1, 0, 1, 2} y B={0, 1, 2, 3, 4, 5, 6}, pero en este caso, tenemos la siguiente relación:
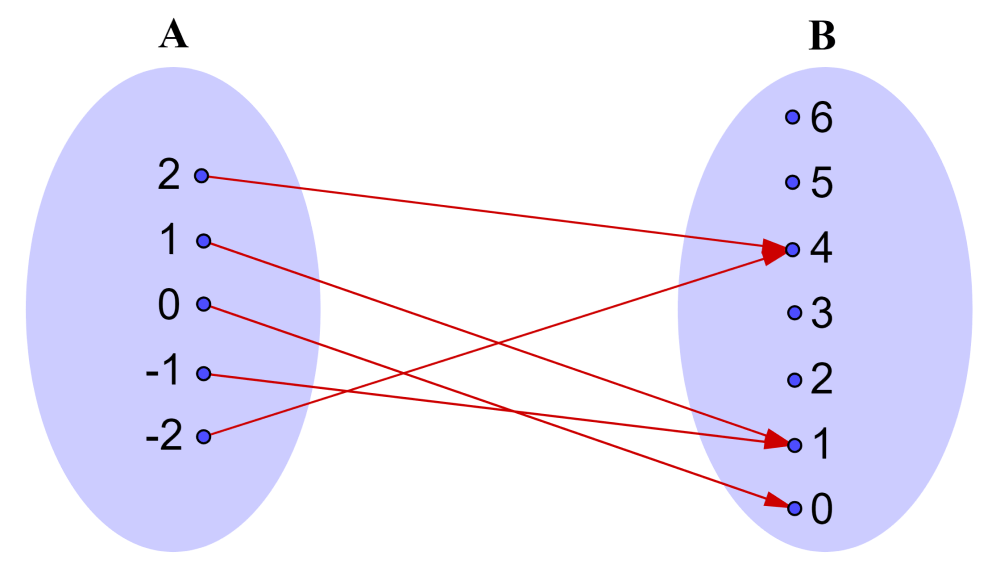
En el caso (ii) observamos que dos elementos del conjunto A se relacionan con un elemento del conjunto B. Esta es una relación dos a uno o una relación muchos a uno.
Una relación muchos a uno también es llamada una función.
Por ejemplo, en la relación que tenemos arriba, la regla es «elevar al cuadrado». Usando la notación de funciones, podemos escribir:
$latex f(x)=x^2~~$ o $latex ~~f:~x\rightarrow x^2$
Ejemplos de relaciones que son funciones
En los siguientes ejemplos, podemos aplicar lo aprendido sobre las relaciones uno a uno y muchos a uno para determinar qué tipo de relación son las siguientes funciones.
EJEMPLO 1
Determina si es que la función $latex f(x)=\frac{x}{2}+2$ es una función uno a uno o muchos a uno.
Solución: La gráfica de la función f es la siguiente:
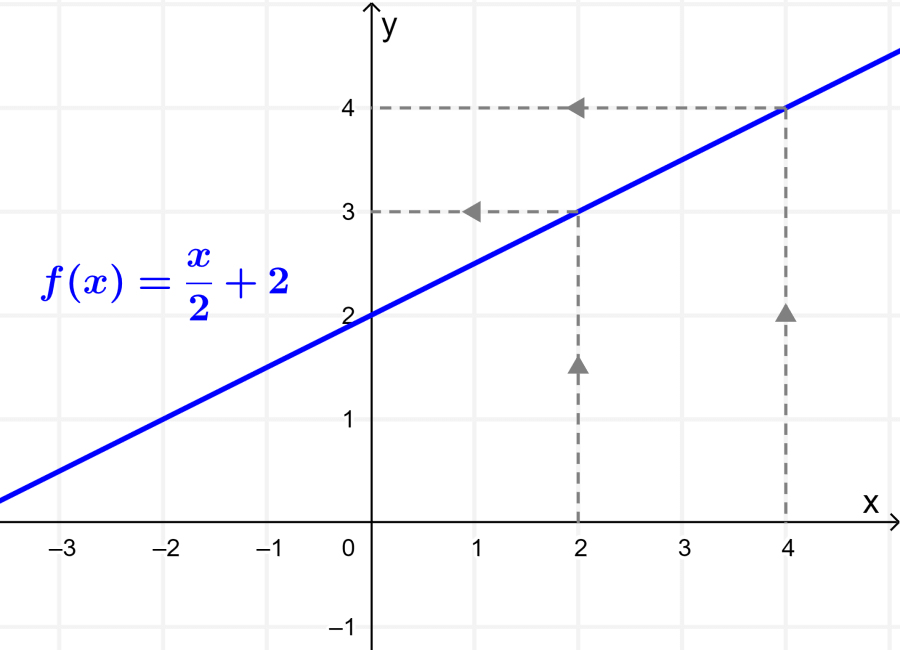
Podemos ver que la gráfica de $latex f(x)=\frac{x}{2}+2$ es una línea recta. Además, vemos claramente que la función es uno a uno, ya que cada valor de x está relacionado con un solo valor de y.
EJEMPLO 2
Determina si es que la función $latex f(x)=x^2+1$ es una función uno a uno o muchos a uno.
Solución: Dado que tenemos $latex f(-1)=(-1)^2+1=2$ y $latex f(1)=1^2+1=2$, sabemos que la función no es uno a uno. Su gráfica es:
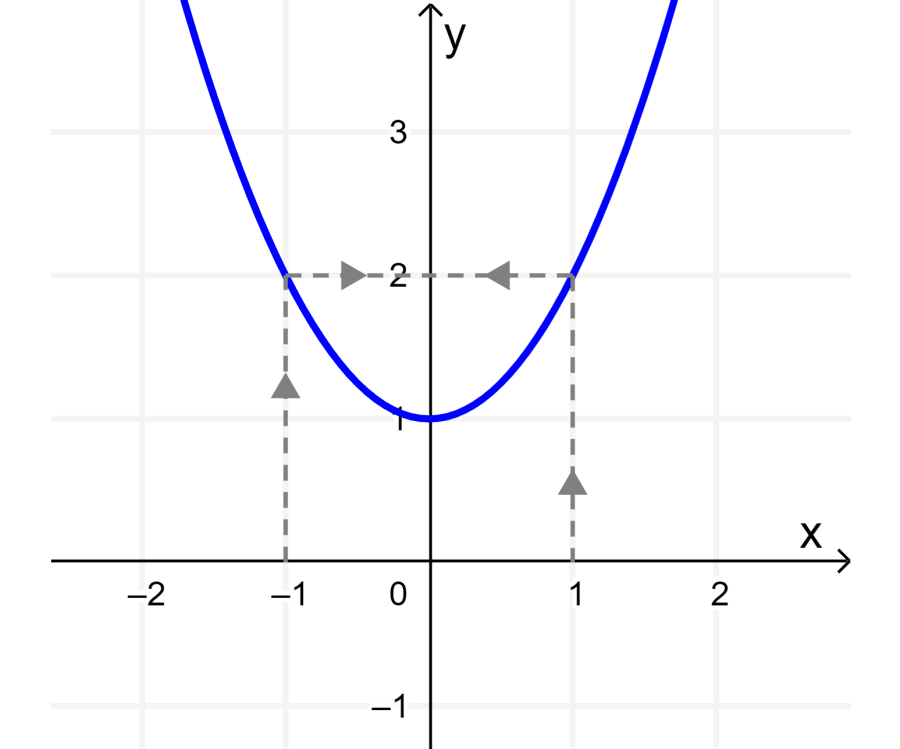
Mirando la gráfica de la función, vemos que esta función es muchos a uno, específicamente, dos a uno.
EJEMPLO 3
¿Es la función $latex f(x)=(x^4+1)^2-3$ una función uno a uno o muchos a uno?
Solución: Una forma de determinar si una función es muchos a uno es usando la prueba $latex f(-1)=f(1)$. Entonces, tenemos:
$latex f(1)=(1^4+1)^2-3$
$latex =(2)^2-3$
$latex =4-3$
$latex =1$
$latex f(-1)=((-1)^4+1)^2-3$
$latex =(2)^2-3$
$latex =4-3$
$latex =1$
Vemos que $latex f(-1)=f(1)$ es verdadero. Esto significa que la función es muchos a uno.
Nota: Ten en cuenta que la prueba $latex f(-1)=f(1)$ funciona solo cuando la función es simétrica con respecto al eje y.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
