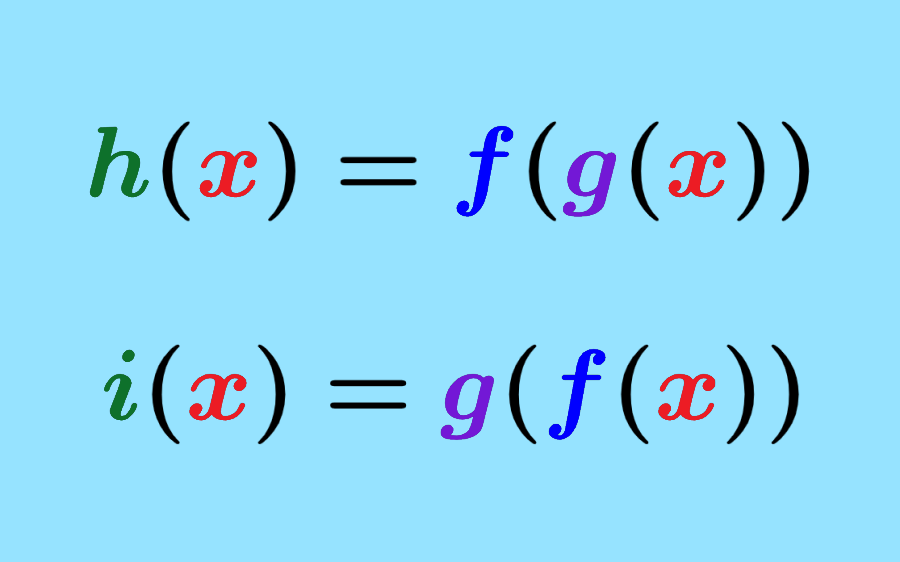Las funciones compuestas son funciones en las que usamos los valores de salida o los resultados de una función en las entradas de otra función. Por ejemplo, si es que tenemos las funciones f(x) y g(x), una función compuesta es formada a escribir f(g(x)). Esencialmente, estamos aplicando una función al resultado de otra función.
A continuación, veremos 10 ejercicios resueltos de funciones compuestas. Además, también podrás practicar tus habilidades con 5 ejercicios de práctica.
10 Ejercicios de funciones compuestas resueltos
Los siguientes ejercicios de funciones compuestas tienen una solución detallada. Sin embargo, intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el valor de $latex f(g(3))$ si es que tenemos las funciones $latex f(x)=2x+5$ y $latex g(x)=x+6$.
Solución
Podemos resolver este ejercicio al empezar evaluando $latex g(3)$. Entonces, tenemos:
$latex g(3)=(3)+6$
$latex g(3)=9$
Ahora que conocemos el valor de $latex g(3)$, podemos usarlo en $latex f(g(3))$:
$latex f(g(3))=f(9)$
$latex =2(9)+5$
$latex f(g(3))=23$
EJERCICIO 2
¿Cuál es el valor de $latex g(f(-3))$ si es que tenemos las funciones $latex f(x)=x^2-5$ y $latex g(x)=2x-7$?
Solución
En este caso, tenemos que evaluar en el orden opuesto en comparación con el anterior ejercicio. Entonces, empezamos evaluando $latex f(-3)$:
$latex f(-3)=(-3)^2-5$
$latex f(-3)=4$
Usando el valor de $latex f(-3)$ en la composición $latex g(f(-3))$, tenemos:
$$g(x)=2x-7$$
$$g(4)=2(4)-7$$
$$g(4)=8-7$$
$$g(4)=1$$
EJERCICIO 3
Si es que tenemos las funciones $latex f(x)=2x+7$ y $latex g(x)=4x-6$, encuentra la función compuesta $latex h(x)=f(g(x))$.
Solución
Para encontrar la composición de funciones $latex f(g(x))$, usamos a la expresión de la función $latex g(x)$ como entrada de la función $latex f(x)$. Entonces, tenemos:
$latex h(x)=f(g(x))$
$latex =f(4x-6)$
$latex =2(4x-6)+7$
$latex =8x-12+7$
$latex h(x)=8x-5$
EJERCICIO 4
Encuentra la función compuesta $latex h(x)=g(f(x))$ si es que $latex f(x)=2x^2+2$ y $latex g(x)=5x-4$.
Solución
En este caso, para encontrar la composición $latex g(f(x))$, tenemos que al usar a la función $latex f(x)$ como la entrada de $latex g(x)$. Entonces, tenemos:
$latex h(x)=g(f(x))$
$latex =g(2x^2+2)$
$latex =5(2x^2+2)-4$
$latex =10x^2+10-4$
$latex h(x)=10x^2+6$
EJERCICIO 5
Determina el valor de $latex f(g(-4))$ si es que tenemos las funciones $latex f(x)=x^2+2x+3$ y $latex g(x)=3x+8$.
Solución
Para encontrar el valor de $latex f(g(-4))$, tenemos que empezar evaluando $latex g(-4)$. Entonces, tenemos:
$latex g(-4)=3(-4)+8$
$latex g(-4)=-4$
Ahora, tenemos que usar el valor de g(-4) en la función f:
$latex f(g(-4))=f(-4)$
$latex =(-4)^2+2(-4)+3$
$latex f(g(-4))=11$
EJERCICIO 6
Encuentra la composición $latex h(x)=f(g(x))$ con las funciones $latex f(x)=-x^2+5x-10$ y $latex g(x)=x+2$.
Solución
La composición $latex f(g(x))$ es encontrada al usar a la función $latex g(x)$ como la entrada de la función $latex f(x)$. Entonces, tenemos:
$latex h(x)=f(g(x))$
$latex =f(x+2)$
$latex =-(x+2)^2+5(x+2)-10$
$latex =-x^2-4x-4+5x+10-10$
$latex h(x)=-x^2+x-4$
EJERCICIO 7
Si es que tenemos la función $latex f(x)=3x^2-20$, ¿cuál es el valor de $latex f(f(3))$?
Solución
En este caso, tenemos la composición de una sola función. Esta composición es similar a las anteriores, con la única diferencia que usamos la misma función dos veces. Entonces, tenemos:
$latex f(3)=3(3)^2-20$
$latex =3(3)^2-20$
$latex =3(9)-20$
$latex f(3)=7$
Ahora, usamos el valor encontrado como la entrada de la función f:
$latex f(f(3)=f(7)$
$latex =3(7)^2-20$
$latex =3(49)-20$
$latex =147-20$
$latex =127$
EJERCICIO 8
Encuentra la composición $latex h(x)=g(g(x))$ si es que tenemos la función $latex g(x)=x^2-5$
Solución
Tenemos una composición con la misma función. Sin embargo, para resolver, tenemos que seguir el mismo proceso.
La composición $latex g(g(x))$ es encontrada al usar a la función $latex g(x)$ como la entrada de la misma función $latex g(x)$. Entonces, tenemos:
$latex h(x)=g(g(x))$
$latex =g(x^2-5)$
$latex =(x^2-5)^2-5$
$latex =x^4-10x^2+25-5$
$latex h(x)=x^4-10x^2+20$
EJERCICIO 9
Si es que tenemos las funciones $latex f(x)=3x+4$, $latex g(x)=5x-6$ y $latex h(x)=-x+4$, ¿cuál es el valor de $latex f(g(h(2)))$?
Solución
En este caso, tenemos una composición de tres funciones. Entonces, empezamos encontrando el valor de $latex h(2)$:
$latex f(2)=-2+4$
$latex f(2)=2$
Ahora, usamos el valor de $latex f(2)$ para encontrar el valor de $latex g(h(2))$:
$latex g(h(2))=g(2)$
$latex =5(2)-6$
$latex =4$
Por último, usamos el valor de $latex g(h(2))$ en la función f:
$latex f(g(h(2)))=f(4)$
$latex =3(4)+4$
$latex =16$
EJERCICIO 10
Si es que tenemos las funciones $latex f(x)=3x+4$, $latex g(x)=5x-6$ y $latex h(x)=-x+4$, encuentra una expresión para $latex i(x)=f(g(h(x)))$.
Solución
Empezamos encontrando una expresión para $latex g(h(x))$:
$latex g(h(x))=5(-x+4)-6$
$latex =-5x+20-6$
$latex =-5x+14$
Ahora, usamos $latex g(h(x))=-5x+14$ en la función f:
$latex i(x)=f(g(h(x)))$
$latex =f(-5x+14)$
$latex =3(-5x+14)+4$
$latex =-15x+42+4$
$latex i(x)=-15x+46$
5 Ejercicios de funciones compuestas para resolver
Aplica todo lo aprendido sobre las funciones compuestas para resolver los siguientes ejercicios.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
