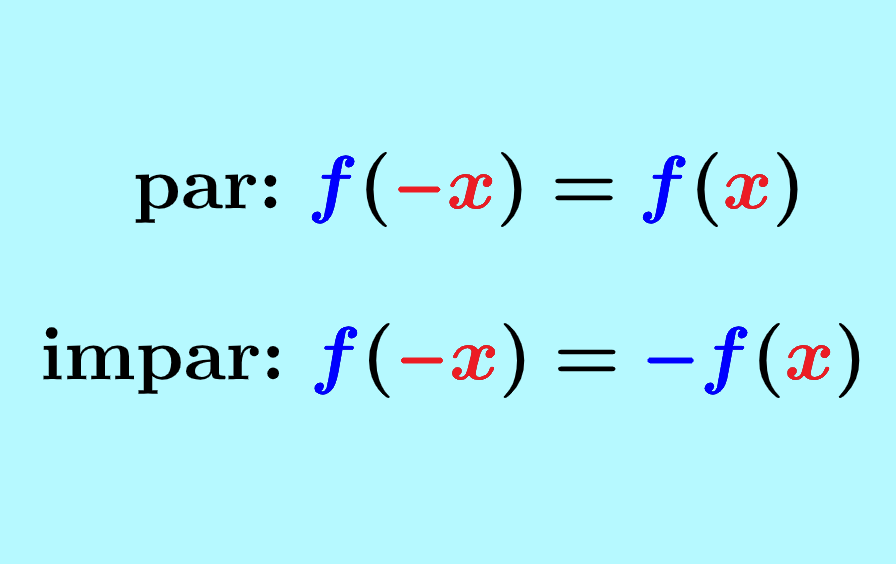Las funciones par e impar son dos funciones con características importantes. Una función par presenta simetría con respecto al eje y. Por otro lado, la función impar tiene simetría rotacional de 180° con respecto al origen. Es posible determinar si es que una función es par o impar usando métodos algebraicos.
A continuación, aprenderemos todo lo relacionado con las funciones par e impar. Veremos sus gráficas, algunas características importantes y conoceremos cómo determinar si una función es par o impar.
Características y gráfica de la función par
Las funciones pares tienen la característica principal de que son simétricas con respecto al eje y. Esto significa que si es que doblamos a la gráfica en el eje y, obtenemos dos partes iguales de la gráfica.
Una función par importante es la función $latex f(x)=x^2$, la cual tiene la siguiente gráfica:
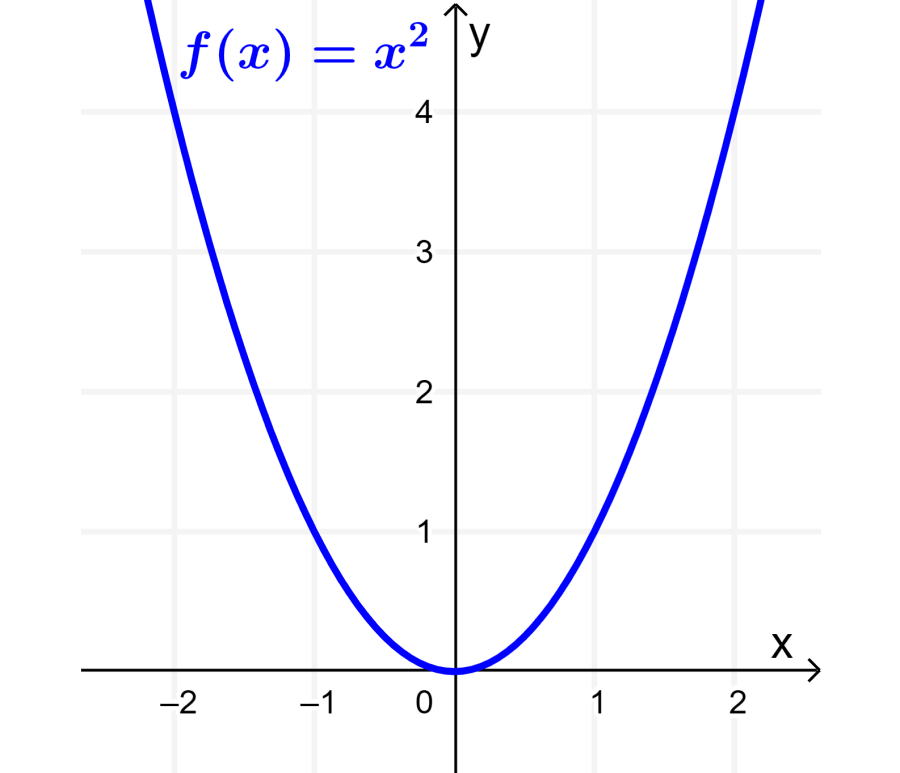
Otros ejemplos de funciones pares son las siguientes funciones:
- $latex f(x)=\cos(x)$
- $latex f(x)=x^4$
- $latex f(x)=\sin^2(x)$
Fórmula de funciones pares
Para determinar si una función es par o no, podemos usar la siguiente fórmula:
$latex f(-x)=f(x)$
Esto significa que, si es que al reemplazar los valores de x en la función por –x obtenemos a la función original, la función es par.
Características y gráfica de la función impar
La característica principal de las funciones impares es que tienen simetría rotacional de 180° con respecto al origen. Esto significa que, si es que rotamos 180° a la gráfica con respecto al punto (0, 0), la gráfica no sufrirá ningún cambio.
Una función impar importante es la función $latex f(x)=x^3$, la cual tiene la siguiente gráfica:
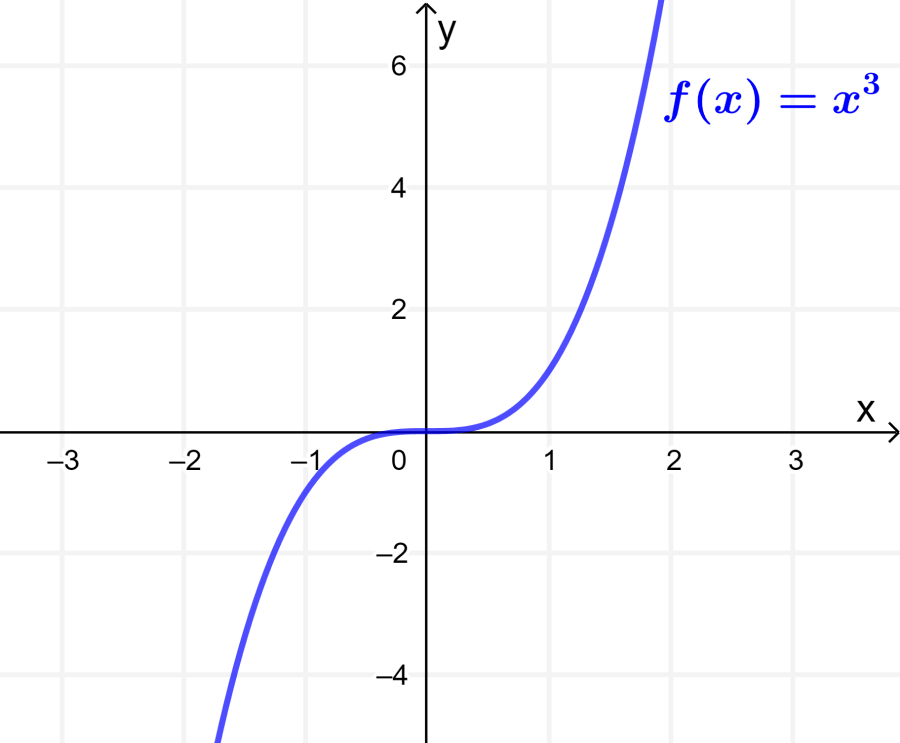
Otros ejemplos de funciones impares son las siguientes funciones:
- $latex f(x)=\sin(x)$
- $latex f(x)=x^5$
- $latex f(x)=x^7$
Fórmula de funciones impares
Podemos determinar si es que una función es par o impar usando la siguiente fórmula:
$latex f(-x)=-f(x)$
Esto significa que, si es que al reemplazar los valores de x en la función por –x obtenemos a la función original multiplicada por -1, la función es impar.
Ejemplos de funciones pares e impares
En los siguientes ejemplos, podemos aplicar lo aprendido sobre el rango de una función. Cada uno de los ejemplos tiene una solución detallada usando la gráfica de la función.
EJEMPLO 1
Determina si es que la función $latex f(x)={{x}^2}+1$ es par o impar.
Solución: Para que una función sea par, la condición $latex f(-x)=f(x)$ debe cumplirse. Entonces, vamos a verificar esto:
$latex f(-x)= (-x)^2+1$
$latex f(-x)= x^2+1$
Vemos que obtuvimos la función original. Entonces, la función sí es par. La siguiente es su gráfica y podemos verificar que sí es par, ya que es simétrica con respecto al eje y.
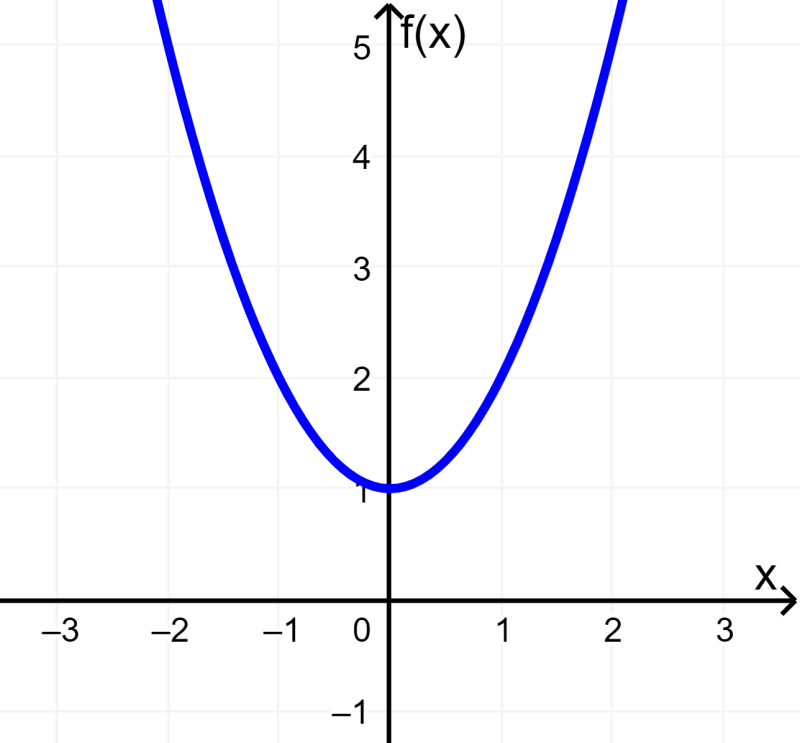
EJEMPLO 2
¿La función $latex f(x)=3x^2-|x|$ es par o impar?
Solución: Podemos determinar si la función es par o impar realizando las pruebas $latex f(-x)=f(x)$ para funciones pares y $latex f(-x)=-f(x)$ para funciones impares.
Empezando con la prueba de funciones pares, tenemos:
$latex f(-x)=3(-x)^2-|-x|$
$latex f(-x)=3x^2-|x|$
Vemos que la expresión obtenida es igual a la función original $latex f(x)$, por lo que la función es par.
Dado que la función es par, ya no tenemos que realizar la prueba de funciones impares.
EJEMPLO 3
Determina si es que la función $latex f(x)=\frac{3}{x}+2x$ es par o impar.
Solución: Para resolver este problema, podemos aplicar la prueba de funciones pares y luego realizar la prueba de funciones impares.
Si es que la función es par, debemos tener $latex f(-x)=f(x)$. Entonces, tenemos:
$latex f(-x)=\frac{3}{-x}+2(-x)$
$latex f(-x)=-\frac{3}{x}-2x$
Esta función no es par porque la expresión obtenida no es igual a la función original $latex f(x)$.
Mirando la expresión obtenida, vemos que es igual a $latex -f(x)$. Esto significa que la función es porque $latex f(-x)=-f(x)$.
EJEMPLO 4
¿Es la función $latex f(x)=(x^3-5)^2$ par, impar o ninguno?
Solución: Usando la prueba de funciones pares, $latex f(-x)=f(x)$, tenemos:
$latex f(-x)=((-x)^3-5)^2$
$latex f(-x)=(-x^3-5)^2$
La expresión que obtuvimos no es igual a $latex f(x)$, por lo que la función no es par. Entonces, continuamos con la prueba de funciones impares.
Para verificar si la función es impar, debemos tener $latex f(-x)=-f(x)$. Sin embargo, la función tampoco es impar, ya que la expresión obtenida arriba no es igual a $latex -f(x)$.
Nota: $latex -f(x)$ sería igual a $latex -(x^3-5)^2$.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
