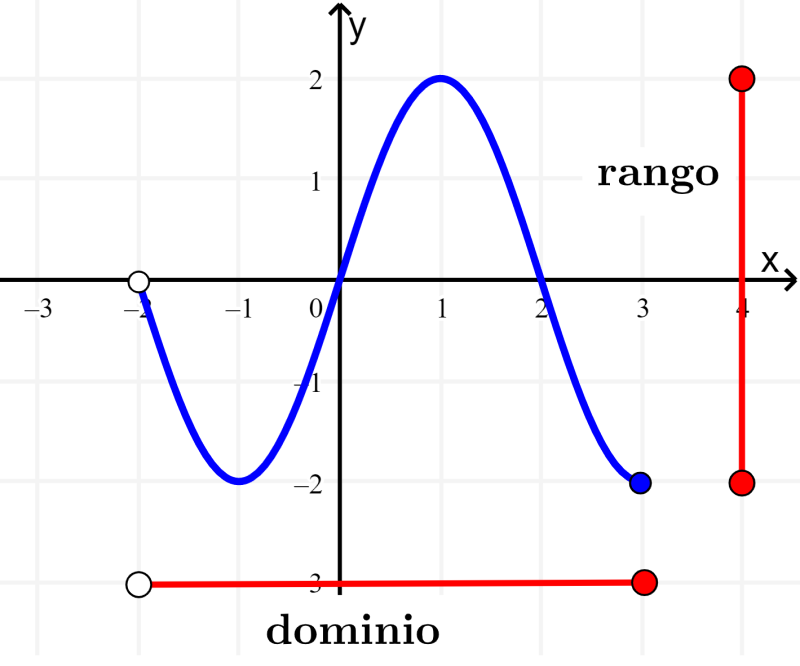
El rango de una función puede ser encontrado al graficar la función e identificar a todos los valores de y que son posibles con el dominio de la función. En algunas funciones como las funciones lineales, funciones cúbicas o la función tangente, el rango de la función es igual a todos los números reales.
A continuación, conoceremos cómo encontrar el rango de una función usando su gráfica. Veremos algunos ejemplos para ilustrar el proceso usado.
Método para encontrar el rango de una función
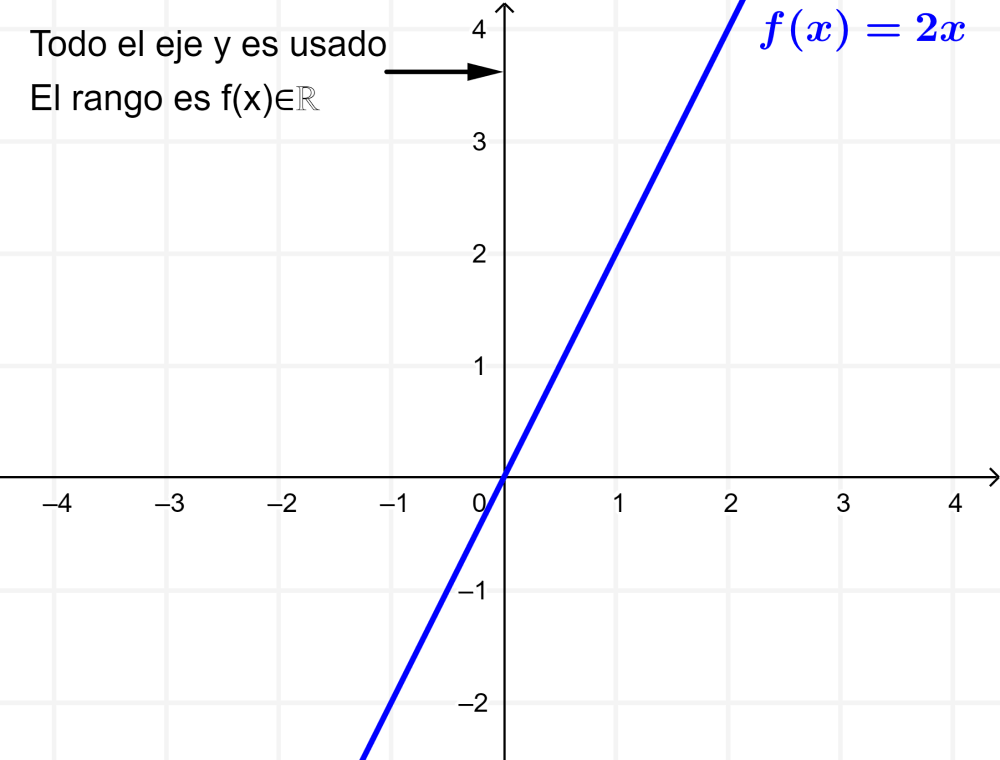
Para encontrar el rango de una función, siempre es útil trazar una gráfica simple de la función. Por ejemplo, supongamos que tenemos la función $latex f(x)=2x$, la cual está definida para todos los valores reales de x. Entonces, la siguiente es su gráfica:
El rango de la función $latex f(x)$ es el conjunto de todos los valores de salida de la función. Es decir, el rango es la parte del eje y que es usado por la función. En esta función, el rango es el conjunto de todos los números reales.
Para indicar que el rango es todos los números reales, podemos escribir
{$latex f(x):f(x)\in \mathbb{R}$}
o simplemente, podemos escribir $latex f(x) \in \mathbb{R}$.
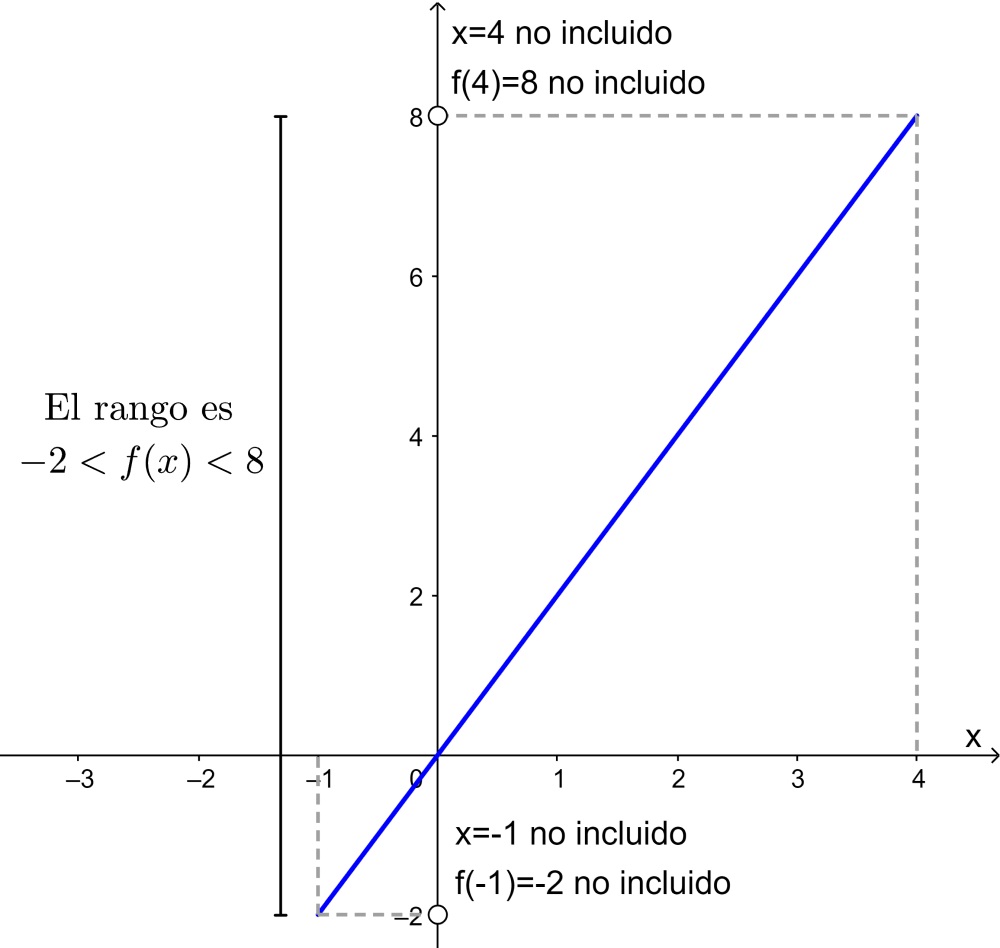
Cuando una función está definida por un dominio restringido, el rango de la función podría también estar restringido. Por ejemplo, consideremos a la siguiente función y su gráfica:
$latex f(x)=2x$, $latex ~~-1<x<4$
El rango de la función es el conjunto de números reales desde -2 hasta 8, excluyendo a -2 y a 8, ya que -1 y 4 están excluidos del dominio de la función. Escribimos a este rango como
$latex -2<f(x)<8$
Ejemplos de rango de funciones
En los siguientes ejemplos, podemos aplicar lo aprendido sobre el rango de una función. Cada uno de los ejemplos tiene una solución detallada usando la gráfica de la función.
EJEMPLO 1
Encuentra el rango de la función $latex f(x)={{x}^2}+1$.
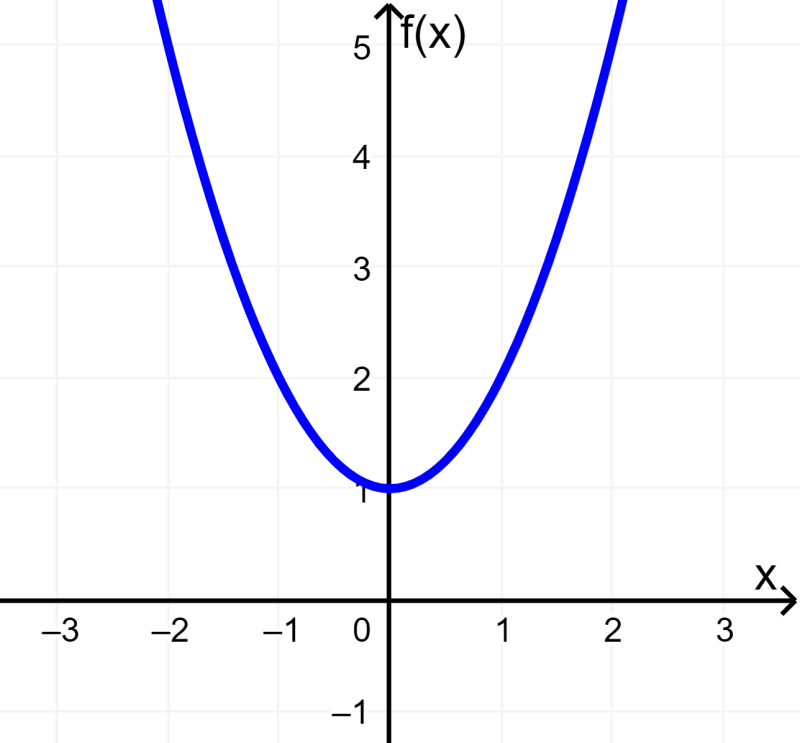
Solución: La función $latex f(x)={{x}^2}+1$ está definida para todos los valores reales de x ya que no hay restricciones en el valor de x. Su gráfica es la siguiente:
Dado que $latex {{x}^2}$ nunca es negativo, $latex {{x}^2}+1$ nunca es menor que 1. Entonces, el rango de $latex f(x)$ es:
“Todos los números reales $latex f(x) \geq 1$”
La gráfica claramente indica que los valores de f(x) nunca son menores que 1.
EJEMPLO 2
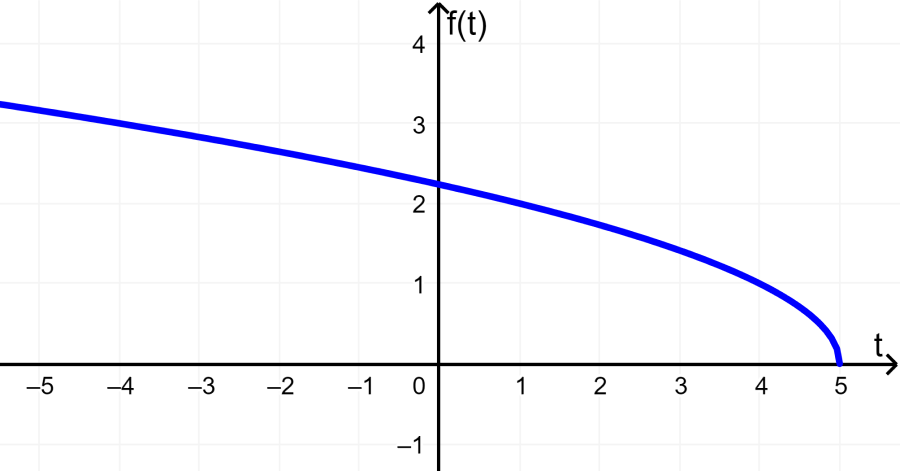
Encuentra el rango de la función $latex f(t)=\sqrt{5-t}$.
Solución: Esta es una función raíz cuadrada. Su gráfica es la siguiente:
Podemos observar que la función $latex f(t)$ no resulta en valores negativos. Entonces, su rango es:
“Todos los números reales, $latex f(t)\geq 0$”
El rango es todos los números reales mayores o iguales a 0.
EJEMPLO 3
¿Cuál es el rango de la función $latex f(x)=2x-1$, para $latex x\geq 0$.
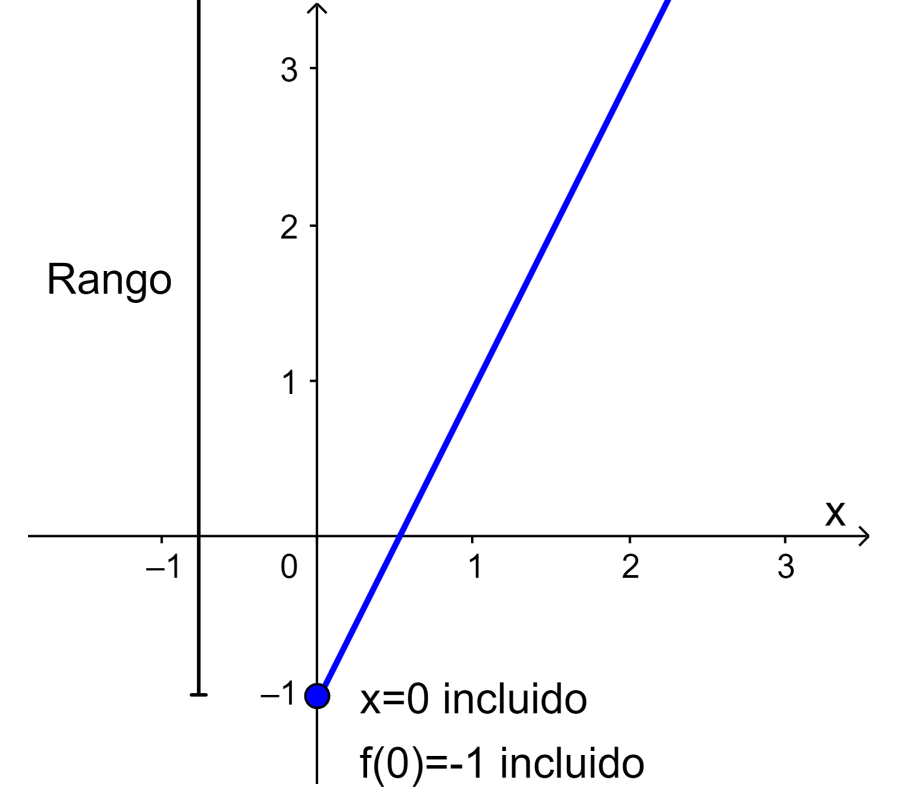
Solución: En este caso, la función $latex f(x)$ tiene los valores de x restringidos a los números iguales o mayores que 0. Entonces, tenemos la siguiente gráfica:
En la gráfica, podemos ver que cuando $latex x\geq 0$, tenemos $latex f(x)\geq -1$. Entonces, el rango de la función es:
“Todos los números reales, $latex f(x)\geq -1$”
EJEMPLO 4
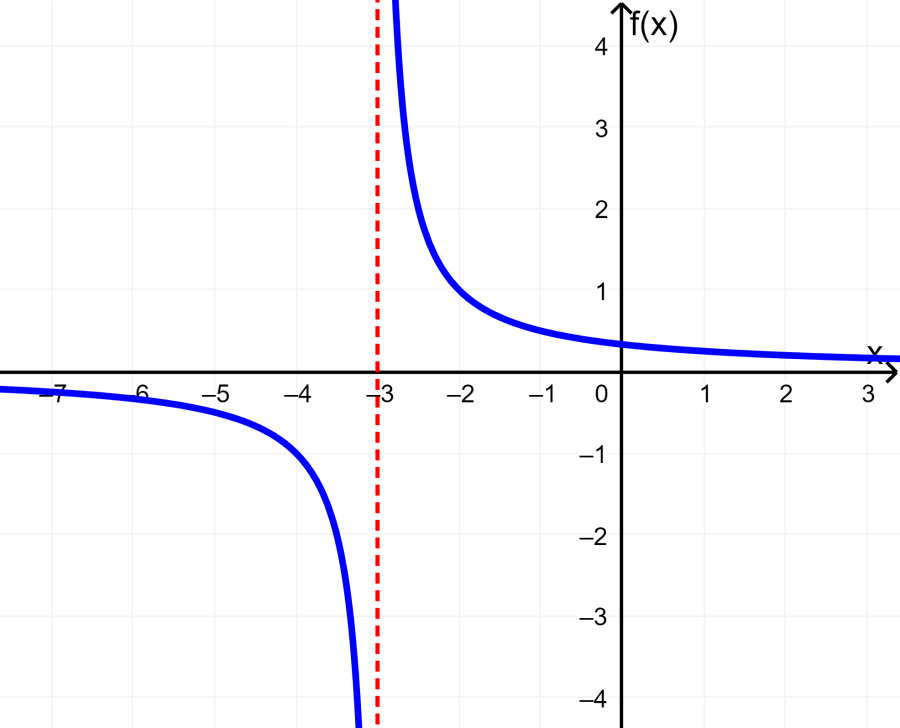
Encuentra el rango de la función $latex f(x)= \frac{1}{x+3}$.
Solución: Esta es una función racional que tiene la siguiente gráfica:
La función $latex f(x)= \frac{1}{x+3}$ no está definida para $latex x=-3$ porque esto produciría una división por cero (tendríamos un 0 en el denominador).
De la gráfica, podemos observar que los valores de $latex f(x)$ pueden ser cualquier valor a excepción del cero. Si es que intentamos resolver la ecuación para y=0, tenemos:
$latex 0= \frac{1}{x+3}$
Multiplicando ambos lados por $latex x+3$, tenemos:
$latex 0= 1$
Esto es imposible. Entonces, el rango de $latex f(x)$ es:
“Todos los números reales excepto el cero”
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
