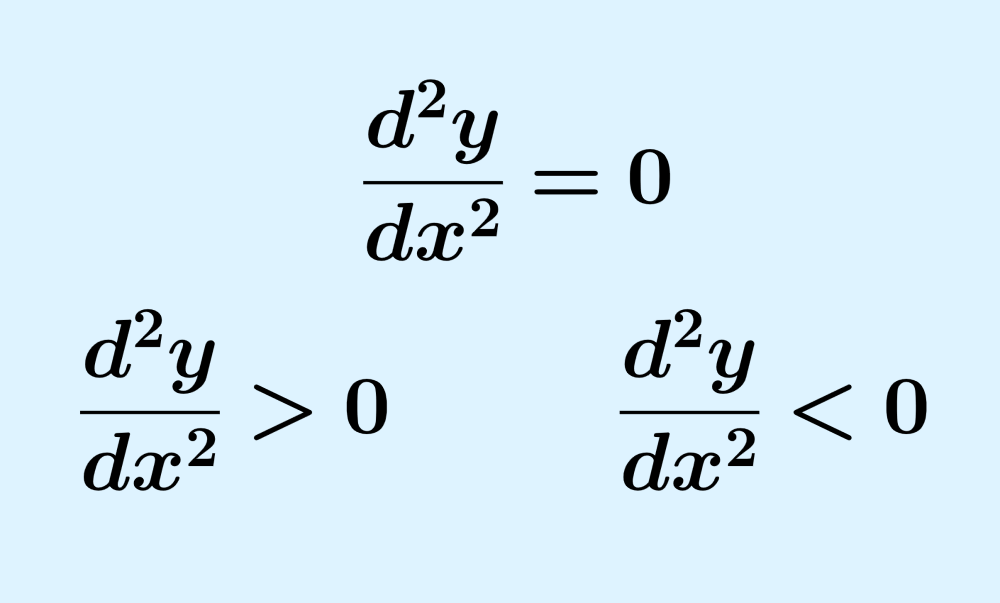El criterio de la segunda derivada es una prueba que nos permite encontrar la naturaleza de los puntos estacionarios de una función. Este criterio nos dice que cuando la segunda derivada en el punto es mayor que 0, el punto es un mínimo. Cuando es menor que 0, el punto es un máximo. Y cuando es igual a 0, el punto podría ser un punto de inflexión.
A continuación, aprenderemos cómo usar el criterio de la segunda derivada para encontrar los puntos máximos, mínimos y puntos de inflexión de una función.
¿Qué es el criterio de la segunda derivada?
El criterio de la segunda derivada es una prueba que nos permite determinar la naturaleza de los puntos estacionarios de una función.
La segunda derivada representa la tasa de variación de la primera derivada. A su vez, la primera derivada es usada para encontrar la pendiente de la curva en un punto específico.
Entonces, la segunda derivada representa la tasa de variación de la pendiente de la función. Podemos representar esto usando el siguiente diagrama:
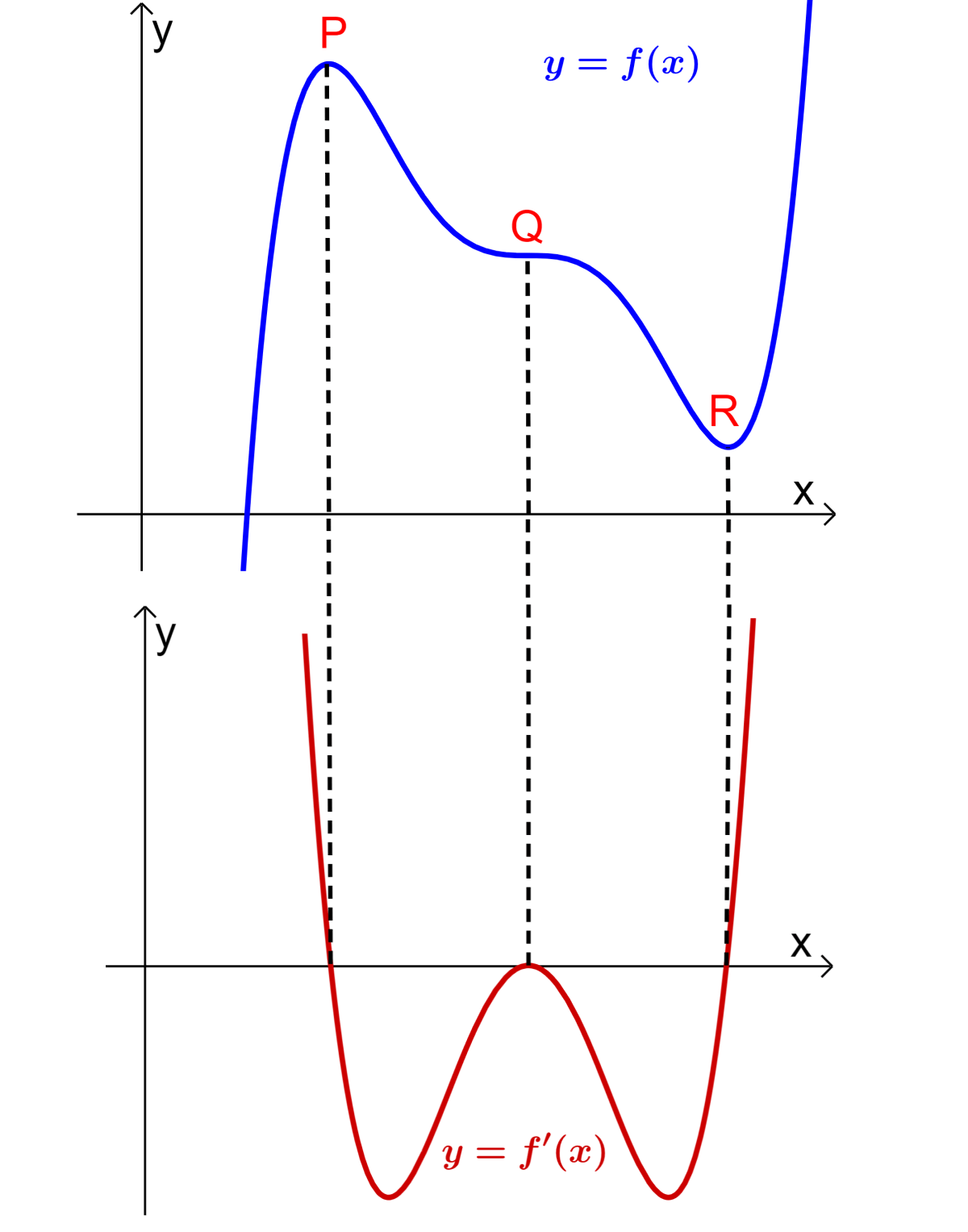
En la parte superior, tenemos la función $latex y=f(x)$, la cual tiene un punto máximo (P), un punto mínimo (R) y un punto de inflexión (Q). En la parte inferior, tenemos la gráfica de la derivada de la función.
- En el punto máximo P, la pendiente de la derivada de la función (la segunda derivada) es negativa. Entonces, tenemos
$latex \frac{d^2y}{dx^2}<0$ en un máximo
- En el punto de inflexión Q, la pendiente de la derivada de la función (la segunda derivada) es cero. Entonces, tenemos
$latex \frac{d^2y}{dx^2}=0$
Nota: Hay casos en los que la segunda derivada podría ser cero en un mínimo o en un máximo. Por esta razón, podemos examinar el signo de la primera derivada en cada lado del punto.
- En el punto mínimo R, la pendiente de la derivada de la función (la segunda derivada) es positiva. Entonces, tenemos
$latex \frac{d^2y}{dx^2}>0$ en un mínimo
En resumen, el criterio de la segunda derivada nos dice que la segunda derivada de la función es negativa en un punto máximo, positiva en un punto mínimo y cero en un punto de inflexión.
Cómo aplicar el criterio de la segunda derivada para encontrar puntos estacionarios
Para encontrar las coordenadas de los puntos estacionarios de una función, tenemos que usar la primera derivada para encontrar estos puntos. Luego usamos la segunda derivada para determinar su naturaleza.
Entonces, encontramos los puntos estacionarios siguiendo estos pasos:
Paso 1: Encontrar la derivada de la función.
Paso 2: Encontrar las coordenadas x de los puntos estacionarios. Para esto, usamos la derivada del paso 1 y formamos una ecuación. Es decir, tenemos $latex \frac{dy}{dx}=0$.
Paso 3: Usar las coordenadas de x de los puntos estacionarios en la función original para encontrar las coordenadas en y.
Paso 4: Los puntos del paso 3 son los puntos estacionarios. Usamos la segunda derivada para determinar la naturaleza de estos puntos.
Cuando $latex \frac{d^2y}{dx^2}<0$, tenemos un punto máximo. Cuando $latex \frac{d^2y}{dx^2}>0$, tenemos un punto mínimo. Cuando $latex \frac{d^2y}{dx^2}=0$, podríamos tener un punto de inflexión (confirmar con la primera derivada).
Ejercicios resueltos del criterio de la segunda derivada
EJERCICIO 1
Encuentra los puntos estacionarios de la función $latex f(x)=-x^3+3x+1$ y determina su naturaleza.
Solución
Paso 1: Empezamos encontrando la derivada de la función:
$latex f(x)=-x^3+3x+1$
$latex f'(x)=-3x^2+3$
Paso 2: Formando una ecuación con la derivada y resolviendo para x, tenemos:
$latex -3x^2+3=0$
$latex -3x^2=-3$
$latex x=\sqrt{3}$
$latex x_{1}=1~~$ o $latex ~~x_{2}=-1$
Paso 3: Usamos los puntos encontrados en la función para encontrar las coordenadas y:
$latex y_{1}=-(1)^3+3(1)+1$
$latex y_{1}=3$
$latex y_{2}=-(-1)^3+3(-1)+1$
$latex y_{2}=-1$
Los puntos estacionarios son (1, 3) y (-1, -1).
Paso 4: Usamos la segunda derivada para determinar la naturaleza de los dos puntos estacionarios encontrados:
$latex f^{\prime \prime}(x)=-6x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)<0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)>0$.
Entonces, el punto máximo es (1, 3) y el punto mínimo es (-1, -1).
EJERCICIO 2
Encuentra los puntos estacionarios de $latex f(x)=2x^3-6x$ y determina su naturaleza.
Solución
Paso 1: La derivada de la función es:
$latex f(x)=2x^3-6x$
$latex f'(x)=6x^2-6$
Paso 2: Formamos una ecuación con la derivada para encontrar los valores x de los puntos estacionarios:
$latex 6x^2-6=0$
$latex 6x^2=6$
$latex x^2=\sqrt{1}$
$latex x_{1}=1~~$ o $latex ~~x_{2}=-1$
Paso 3: Usando los valores de x en la función, encontramos los valores de y:
$latex y_{1}=2(1)^3-6(1)$
$latex y_{1}=-4$
$latex y_{2}=2(-1)^3-6(-1)$
$latex y_{2}=4$
Paso 4: Ahora, usamos la segunda derivada para determinar la naturaleza de estos puntos:
$latex f^{\prime \prime}(x)=12x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$.
El punto mínimo es (1, -4) y el punto máximo es (-1, 4).
EJERCICIO 3
¿Cuáles son los puntos estacionarios de la función $latex g(x)=x^3 – 3x^2 + 3x+1$?
Solución
Paso 1: La derivada de la función dada es:
$latex g(x)=x^3 – 3x^2 + 3x+1$
$latex g'(x)=3x^2-6x+3$
Paso 2: Formamos una ecuación con la derivada y resolvemos por factorización para encontrar los puntos estacionarios:
$latex 3x^2-6x+3=0$
$latex 3(x^2-2x+1) = 0$
$latex 3(x-1)(x-1) = 0$
$latex x=1$
Paso 3: Las coordenadas y de los puntos estacionarios son:
$latex y=(1)^3 – 3(1)^2 + 3(1)+1$
$latex y=2$
Paso 4: Ahora, podemos clasificar a los puntos estacionarios usando la segunda derivada de la función:
$latex g^{\prime \prime}(x)=6x-6$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)=0$. Entonces, el punto (1, 2) es un punto de inflexión.
EJERCICIO 4
Encuentra las coordenadas de los puntos estacionarios de la función $latex f(x)=x^3-6x^2-15x+1$.
Solución
Paso 1: Podemos encontrar la derivada de la función de la siguiente forma:
$latex f(x)=x^3-6x^2-15x+1$
$latex f'(x)=3x^2-12x-15$
Paso 2: Encontramos los puntos estacionarios formando una ecuación con la derivada y resolviendo por factorización:
$latex 3x^2-12x-15=0$
$latex 3(x^2-4-5)=0$
$latex 3(x-5)(x+1)=0$
$latex x_{1}=5~~$ o $latex ~~x_{2}=-1$
Paso 3: Las coordenadas y de los puntos son:
$latex y_{1}=(5)^3-6(5)^2-15(5)+1$
$latex y_{1}=-99$
$latex y_{2}=(-1)^3-6(-1)^2-15(-1)+1$
$latex y_{2}=9$
Paso 4: Usando la segunda derivada, determinamos la naturaleza de los puntos encontrados:
$latex f^{\prime \prime}(x)=6x-12$
Cuando $latex x=5$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$.
Entonces, el punto (5, -99) es un punto mínimo y (-1, 9) es un punto máximo.
EJERCICIO 5
¿Cuáles son los puntos estacionarios de $latex f(x)=x^4+4x^3+1$?
Solución
Paso 1: Encontrando la derivada de la función, tenemos:
$latex f(x)=x^4+4x^3+1$
$latex f'(x)=4x^3+12x^2$
Paso 2: Formando una ecuación con la derivada y resolviendo para x, encontramos los puntos estacionarios:
$latex 4x^3+12x^2=0$
$latex 4x^2(x+3)=0$
$latex x_{1}=0~~$ o $latex ~~x_{2}=-3$
Paso 3: Las coordenadas y de los puntos estacionarios son:
$latex y_{1}=(0)^4+4(0)^3+1$
$latex y_{1}=1$
$latex y_{2}=(-3)^4+4(-3)^3+1$
$latex y_{2}=-26$
Paso 4: Usamos la segunda derivada para determinar la naturaleza de los puntos estacionarios:
$latex f^{\prime \prime}(x)=12x^2+24x$
Cuando $latex x=0$, tenemos $latex f^{\prime \prime}(x)=0$ y cuando $latex x=-3$, tenemos $latex f^{\prime \prime}(x)>0$.
El punto $latex x=0$ podría ser un punto de inflexión. Al usar los valores $latex x=0.1$ y $latex x=-0.1$ en la primera derivada, obtenemos pendientes con el mismo signo, por lo que el punto sí es un punto de inflexión.
Las coordenadas del punto de inflexión son (0, 1) y las coordenadas del punto mínimo son (-3, -26).
Criterio de la segunda derivada – Ejercicios para resolver
¿Cuál es el punto mínimo de la función $latex f(x)=-2x^4+10x^2-8$
Escribe las coordenadas en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas y puntos estacionarios? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
