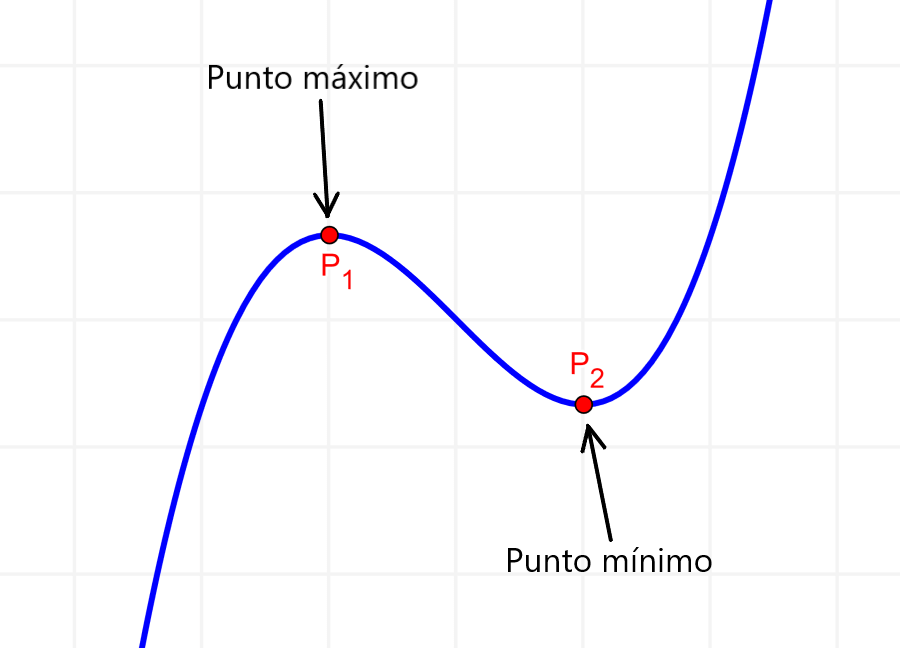
Los puntos máximos y mínimos de una función son puntos estacionarios. Estos puntos pueden ser encontrados formando una ecuación con la derivada de una función. Luego, podemos determinar cuál es un mínimo y cuál es un máximo usando la segunda derivada.
A continuación, resolveremos 10 ejercicios de máximos y mínimos de una función con la segunda derivada. Además, exploraremos 5 problemas de práctica.
CÁLCULO
Relevante para…
Resolver algunos ejercicios de máximos y mínimos de una función.
CÁLCULO

Relevante para…
Resolver algunos ejercicios de máximos y mínimos de una función.
¿Cómo encontrar el punto máximo con la segunda derivada?
Para encontrar el punto máximo de una función, tenemos que empezar usando la primera derivada para determinar todos los puntos estacionarios de la función.
Podemos lograr esto considerando que la pendiente en los puntos estacionarios de una función es igual a cero. Entonces, podemos formar una ecuación con la derivada y encontrar los valores de x.
Luego, usamos la segunda derivada para identificar al punto máximo. En un punto máximo, la segunda derivada es menor que cero, es decir, es negativa.
La segunda derivada es negativa en un punto máximo, ya que la pendiente (la primera derivada) es positiva hasta alcanzar el punto máximo y luego es negativa. Es decir, la derivada decrece cerca al punto máximo como vemos en el diagrama:
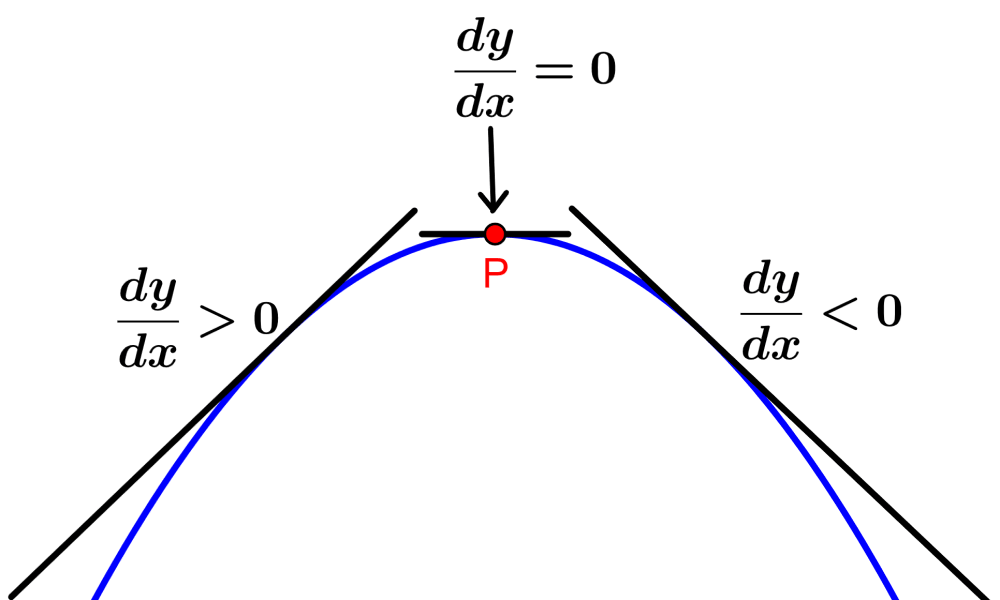
En resumen, encontramos el punto máximo de una función con los siguientes pasos:
Paso 1: Calcular la primera derivada de la función.
Paso 2: Usar la derivada para obtener los puntos estacionarios. Entonces, formamos la ecuación $latex \frac{dy}{dx}=0$ y resolvemos para x.
Paso 3: Usar la segunda derivada para identificar al punto máximo. Para que el punto sea un máximo, debemos tener $latex \frac{d^2y}{dx^2}<0$.
Paso 4: Con la coordenada en x del paso 3, encontramos la coordenada en y del punto máximo.
¿Cómo encontrar el punto mínimo con la segunda derivada?
Para encontrar el punto mínimo de una función, usamos la primera derivada para encontrar los puntos estacionarios. Entonces, formamos una ecuación con la derivada y resolvemos para x.
Luego, usamos la segunda derivada para identificar al punto mínimo. En un punto mínimo, la segunda derivada es mayor que cero, es decir, es positiva.
La segunda derivada es positiva en un punto mínimo, ya que la pendiente (la primera derivada) es negativa hasta alcanzar el punto mínimo y luego es positiva. Es decir, la derivada crece cerca al punto máximo como vemos en el diagrama:
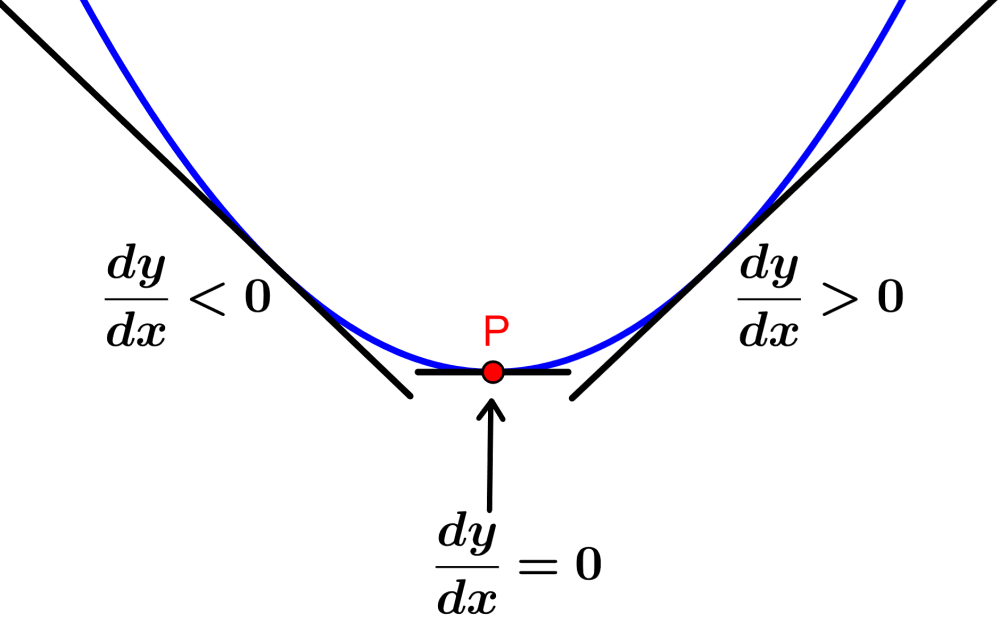
En resumen, podemos encontrar las coordenadas del punto mínimo de una función con los siguientes pasos:
Paso 1: Calcular la primera derivada de la función.
Paso 2: Encontrar los puntos estacionarios usando la derivada. Para esto, formamos la ecuación $latex \frac{dy}{dx}=0$ y resolvemos para x.
Paso 3: Usar la segunda derivada para identificar al punto mínimo. Cuando tenemos un punto mínimo, debemos tener $latex \frac{d^2y}{dx^2}>0$.
Paso 4: Usar la coordenada en x del paso 3 para encontrar la coordenada en y del punto mínimo.
10 Ejercicios de máximos y mínimos con la segunda derivada resueltos
EJERCICIO 1
¿Cuáles son las coordenadas del punto máximo de la función $latex f(x)=-x^2+2x$?
Solución
Para encontrar el punto máximo, tenemos que empezar encontrando todos los puntos estacionarios. Para esto, obtenemos la derivada de la función
$latex f(x)=-x^2+2x$
$latex f'(x)=-2x+2$
Ahora, formamos una ecuación con la derivada y encontramos los valores de x:
$latex -2x+2=0$
$latex -2x=-2$
$latex x=1$
El valor encontrado corresponde a un punto estacionario. Para verificar si es que el punto es un punto máximo, usamos la segunda derivada:
$latex f^{\prime \prime}(x)=-2$
Dado que $latex f^{\prime \prime}(x)<0$, el punto encontrado corresponde a un punto máximo.
Usando $latex x=1$ en la función, encontramos la coordenada en y del punto máximo:
$latex y=-x^2+2x$
$latex y=-(1)^2+2(1)$
$latex y=1$
El punto máximo tiene las coordenadas (1, 1).
EJERCICIO 2
¿Cuáles son las coordenadas del punto mínimo de la función $latex f(x)=x^2+2x-1$?
Solución
Empezamos encontrando la derivada de la función, ya que la vamos a usar para encontrar los puntos estacionarios:
$latex f(x)=x^2+2x-1$
$latex f'(x)=2x+2$
Formamos una ecuación con la derivada y resolvemos para x:
$latex 2x+2=0$
$latex 2x=-2$
$latex x=-1$
Ahora, usamos la segunda derivada para verificar si el punto es un punto mínimo.
$latex f^{\prime \prime}(x)=2$
Dado que tenemos $latex f^{\prime \prime}(x)>0$, el punto encontrado corresponde a un punto mínimo.
Finalmente, usamos $latex x=-1$ en la función para determinar la coordenada en y del punto:
$latex y=x^2+2x-1$
$latex y=(-1)^2+2(-1)-1$
$latex y=-2$
El punto mínimo de la función es (-1, -2).
EJERCICIO 3
Determina el punto máximo de la función $latex f(x)=-x^3+3x+2$.
Solución
Empezamos encontrando la derivada de la función:
$latex f(x)=-x^3+3x+2$
$latex f'(x)=-3x^2+3$
Formando una ecuación con la derivada, podemos resolver para x para encontrar los puntos estacionarios:
$latex -3x^2+3=0$
$latex -3x^2=-3$
$latex x=\sqrt{3}$
$latex x=1~~$ o $latex ~~x=-1$
Usando la segunda derivada, podemos determinar la naturaleza de los puntos encontrados:
$latex f^{\prime \prime}(x)=-6x$
Si es que $latex x=1$, tenemos $latex f^{\prime \prime}(x)<0$, y si es que $latex x=-1$, tenemos $latex f^{\prime \prime}(x)>0$. Entonces, $latex x=1$ es el punto máximo.
Usamos $latex x=1$ para encontrar la coordenada en y del punto máximo:
$latex y=-x^3+3x+2$
$latex y=-(1)^3+3(1)+2$
$latex y=4$
El punto máximo tiene las coordenadas (1, 4).
EJERCICIO 4
Encuentra las coordenadas del punto mínimo de la función $latex f(x)=x^3-3x-2$.
Solución
La derivada de la función es la siguiente:
$latex f(x)=x^3-3x-2$
$latex f'(x)=3x^2-3$
Ahora, usamos la derivada, formamos una ecuación y resolvemos para x:
$latex 3x^2-3=0$
$latex x=\sqrt{1}$
$latex x=\pm 1$
$latex x=1~~$ o $latex ~~x=-1$
Encontramos dos puntos estacionarios. Entonces, tenemos que usar la segunda derivada para determinar la naturaleza de estos puntos:
$latex f^{\prime \prime}(x)=6x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$. Entonces, $latex x=1$ es el punto mínimo.
Encontramos la coordenada en y del punto mínimo usando $latex x=1$ en la función:
$latex y=x^3-3x-2$
$latex y=(1)^3-3(1)-2$
$latex y=-4$
El punto mínimo de la función es (1, -4).
EJERCICIO 5
¿Cuáles son las coordenadas del punto máximo de la función $latex f(x)=2x^3-6x+5$?
Solución
La derivada de la función es:
$latex f(x)=2x^3-6x+5$
$latex f'(x)=6x^2-6$
Podemos encontrar los valores de x de los puntos estacionarios formando una ecuación con la derivada:
$latex 6x^2-6=0$
$latex 6x^2=6$
$latex x^2=\sqrt{1}$
$latex x=1~~$ o $latex ~~x=-1$
Ahora, usamos la segunda derivada para determinar la naturaleza de estos puntos:
$latex f^{\prime \prime}(x)=12x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$, por lo que $latex x=-1$ es el punto máximo.
Encontramos la coordenada en y del punto máximo de la siguiente forma:
$latex y=2x^3-6x$
$latex y=2(-1)^3-6(-1)$
$latex y=4$
El punto máximo tiene las coordenadas (-1, 4).
EJERCICIO 6
Si tenemos la función $latex f(x)=2x^3-6x-4$, encuentra su punto mínimo.
Solución
Encontramos la derivada de la función de la siguiente forma:
$latex f(x)=2x^3-6x-4$
$latex f'(x)=6x^2-6$
Podemos encontrar los puntos estacionarios al formar una ecuación con la derivada y resolver para x:
$latex 6x^2-6=0$
$latex x=\sqrt{1}$
$latex x=\pm 1$
$latex x=1~~$ o $latex ~~x=-1$
Tenemos dos puntos estacionarios, por lo que usamos la segunda derivada para determinar su naturaleza:
$latex f^{\prime \prime}(x)=12x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$. Esto significa que $latex x=1$ es el punto mínimo.
Finalmente, encontramos la coordenada en y del punto:
$latex y=2x^3-6x-4$
$latex y=2(1)^3-6(1)-4$
$latex y=-8$
El punto mínimo de la función es (1, -8).
EJERCICIO 7
Encuentra las coordenadas del punto máximo de $latex f(x)=\frac{1}{3}x^3+x^2-3x$.
Solución
Empezamos encontrando la derivada de la función:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f'(x)=x^2+2x-3$
Ahora, vamos a formar una ecuación con la derivada y resolver por factorización:
$latex x^2+2x-3=0$
$latex (x+3)(x-1)=0$
$latex x=-3~~$ o $latex ~~x=1$
Hemos encontrado dos puntos estacionarios, por lo que podemos usar la segunda derivada para determinar la naturaleza de estos puntos:
$latex f^{\prime \prime}(x)=2x+2$
Cuando $latex x=-3$, tenemos $latex f^{\prime \prime}(x)<0$ y cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$. Entonces, el punto máximo está en $latex x=-3$.
Finalmente, encontramos la coordenada en y del punto usando $latex x=-3$ en la función:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f(x)=\frac{1}{3}(-3)^3+(-3)^2-3(-3)$
$latex y=9$
El punto máximo tiene las coordenadas (-3, 9).
EJERCICIO 8
¿Cuáles son las coordenadas del punto mínimo de la función $latex f(x)=-\frac{1}{3}x^3+x^2+3x$?
Solución
Empezamos encontrando la derivada de la función y formamos una ecuación para obtener los puntos estacionarios:
$latex f(x)=-\frac{1}{3}x^3+x^2+3x$
$latex f'(x)=-x^2+2x+3$
$latex -x^2+2x+3=0$
$latex -(x-3)(x+1)=0$
$latex x=3~~$ o $latex ~~x=-1$
Ahora, usamos la segunda derivada
$latex f^{\prime \prime}(x)=-2x+2$
Cuando $latex x=3$, tenemos $latex f^{\prime \prime}(x)<0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)>0$. Esto significa que $latex x=-1$ es el punto mínimo.
Finalmente, determinamos la coordenada en y del punto mínimo:
$latex y=-\frac{1}{3}x^3+x^2+3x$
$latex y=-\frac{1}{3}(-1)^3+(-1)^2+3(-1)$
$latex y=-\frac{5}{3}$
El punto mínimo de la función es $latex (-1, ~-\frac{5}{3})$.
EJERCICIO 9
En el siguiente triángulo rectángulo ABC, las longitudes de los lados AB y BC varían de forma que su suma siempre es igual a 6 cm. Encuentra el área máxima del triángulo ABC.
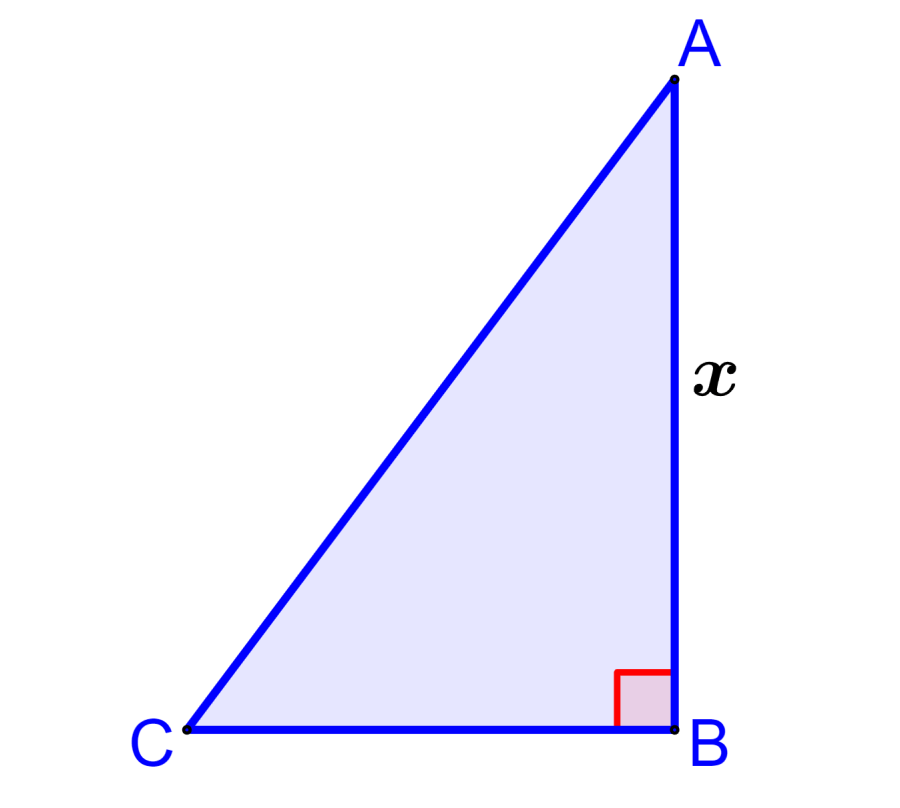
Solución
Podemos resolver este problema al encontrar una función del área en términos de x. Para esto, observamos lo siguiente:
$latex AB+BC=6$
$latex x+BC=6$
$latex BC=6-x$
Entonces, podemos usar la fórmula del área de un triángulo para obtener:
$latex A=\frac{1}{2}\times BC \times AB$
$latex A=\frac{1}{2}(6-x)x$
$latex A=3x-\frac{x^2}{2}$
Ahora, tenemos que encontrar la derivada para formar una ecuación y encontrar los puntos estacionarios:
$latex A(x)=3x-\frac{x^2}{2}$
$latex A'(x)=3-x$
$latex 3-x=0$
$latex x=3$
Verificamos si es que este punto es un punto máximo usando la segunda derivada:
$latex A^{\prime \prime}(x)=-1$
Dado que $latex f^{\prime \prime}(x)<0$, sabemos que el punto es un máximo. Entonces, usamos $latex x=3$ para encontrar el área máxima:
$latex A=3x-\frac{x^2}{2}$
$latex A=3(3)-\frac{(3)^2}{2}$
$latex A=\frac{9}{2}=4.5$
El área máxima del triángulo es 4.5 cm².
EJERCICIO 10
El siguiente triángulo rectángulo ABC tiene lados con longitudes AB=x y BC=x+2. Encuentra el área mínima del triángulo ABC.
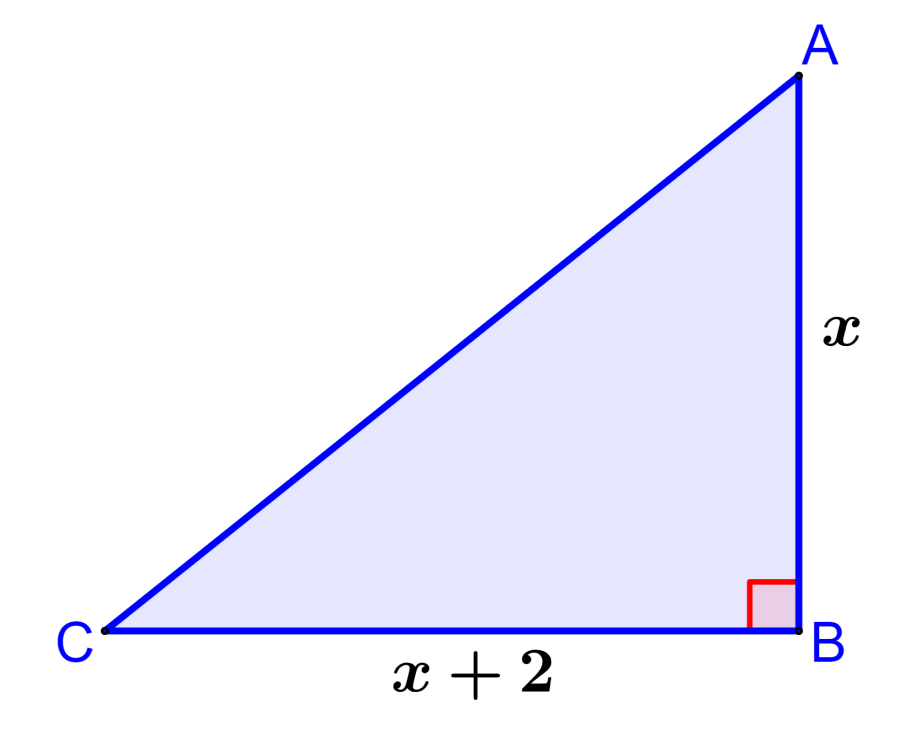
Solución
Similar al ejercicio anterior, tenemos que encontrar una función para el área del triángulo usando la información dada:
$latex A=\frac{1}{2}\times BC \times AB$
$latex A=\frac{1}{2}(x+2)x$
$latex A=\frac{1}{2}x^2+x$
Ahora, encontramos la derivada para formar una ecuación y encontrar los puntos estacionarios:
$latex A(x)=\frac{1}{2}x^2+x$
$latex A'(x)=x+1$
$latex x+1=0$
$latex x=-1$
Para verificar si el punto es un mínimo, vamos a usar la segunda derivada:
$latex A^{\prime \prime}(x)=1$
Tenemos $latex f^{\prime \prime}(x)>0$, por lo que confirmamos que el punto es un mínimo. Entonces, usamos $latex x=-1$ para encontrar el área mínima:
$latex A=\frac{1}{2}x^2+x$
$latex A=\frac{1}{2}(-1)^2-1$
$latex A=-\frac{1}{2}=0.5$
El área mínima del triángulo es 0.5 cm².
Ejercicios de puntos máximos y mínimos para resolver


Encuentra las coordenadas del punto mínimo de $latex f(x)=-1+4x+2x^2$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas y puntos estacionarios? Puedes mirar estas páginas:


