Los máximos, mínimos y puntos de inflexión son denominados puntos estacionarios de una función. Las coordenadas de estos puntos pueden ser encontradas usando la derivada de la función. La pendiente en los máximos, mínimos y puntos de inflexión es igual a cero. Entonces, tenemos que encontrar las raíces de la derivada.
A continuación, aprenderemos sobre los puntos máximos, mínimos y puntos de inflexión de funciones. Además, conoceremos cómo encontrar las coordenadas de estos puntos con ejemplos.
CÁLCULO
Relevante para…
Aprender sobre los puntos máximos, mínimos y puntos de inflexión.
- Definición del punto máximo de una función
- Encontrar las coordenadas del punto máximo de una función
- Definición del punto mínimo de una función
- Encontrar las coordenadas del punto mínimo de una función
- Definición de los puntos de inflexión de una función
- Encontrar las coordenadas de los puntos de inflexión de una función
- Véase también
CÁLCULO
Relevante para…
Aprender sobre los puntos máximos, mínimos y puntos de inflexión.
Definición del punto máximo de una función
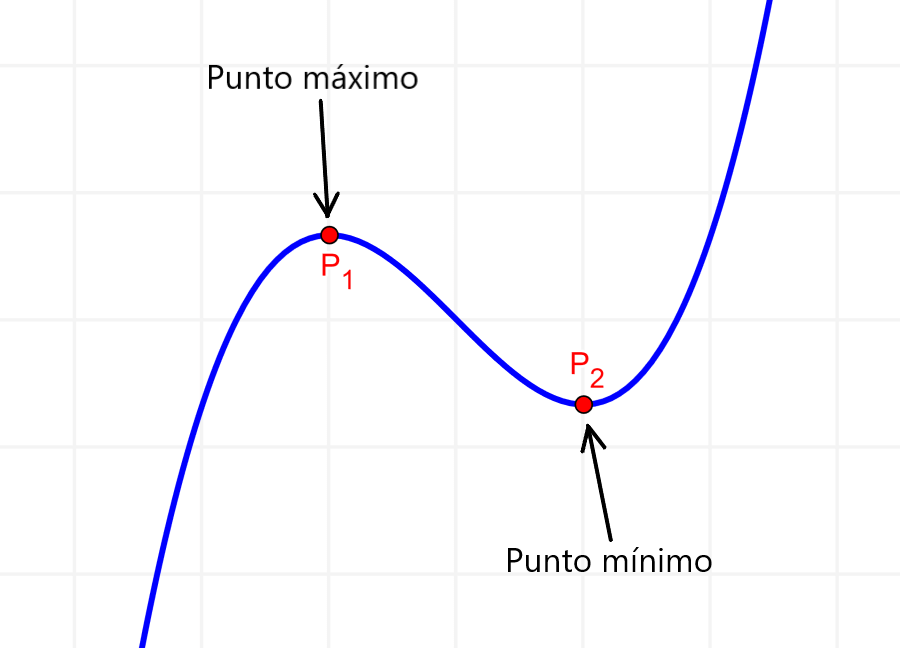
Los puntos máximos de funciones son puntos en donde los valores de y de la función son los más altos posibles que las funciones pueden alcanzar. Es decir, no existe otro punto en la función que tenga un valor de y mayor.
El punto máximo de una función es uno de los puntos estacionarios de la función. En estos puntos, la pendiente de la recta tangente es igual a cero. Eso significa que tenemos $latex \frac{dy}{dx}=0$.
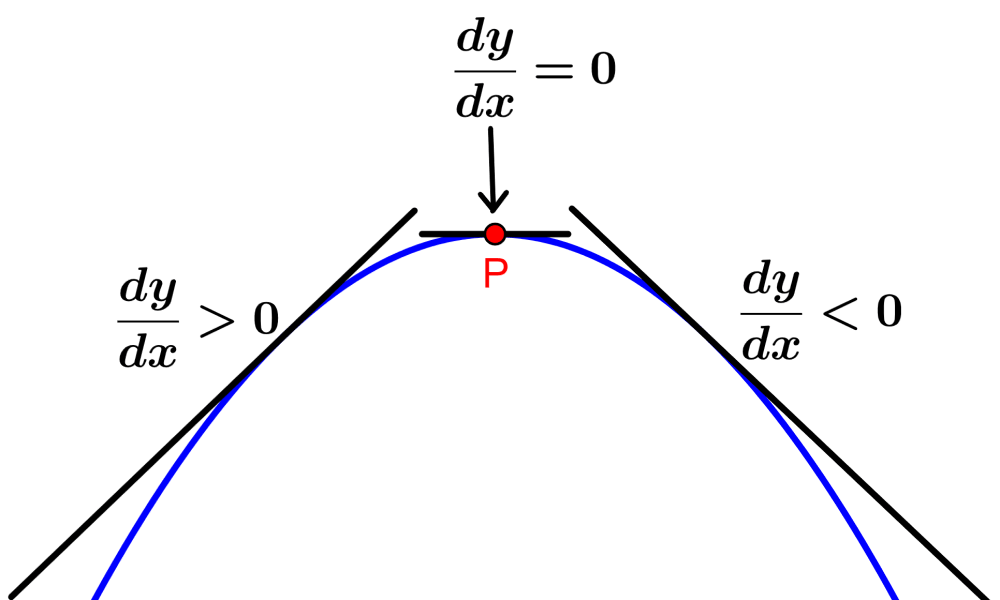
Podemos usar el siguiente diagrama para tener una representación gráfica de un punto máximo de una función:
En la parte izquierda de un punto máximo, la pendiente es positiva y en la parte derecha del punto máximo, la pendiente es negativa. Es decir, la función crece hasta que alcanza el punto máximo y luego decrece. Entonces, tenemos:
- En la parte izquierda de P: $latex \frac{dy}{dx}>0$
- En el punto P: $latex \frac{dy}{dx}=0$
- En la parte derecha de P: $latex \frac{dy}{dx}<0$
Dado que la pendiente (el valor de la derivada) va de positiva a negativa cerca al punto máximo, la segunda derivada de la función en un punto máximo es negativa (la primera derivada decrece).
Encontrar las coordenadas del punto máximo de una función
Podemos encontrar las coordenadas de un punto máximo al usar la derivada de la función. Para esto, consideramos que la pendiente en un punto máximo es igual a cero.
Entonces, formamos una ecuación con la derivada y encontramos sus raíces (los valores de x). Luego, usamos la segunda derivada para identificar cuál de esos valores es el punto máximo.
Si es que conocemos la función, podemos encontrar su punto máximo con los siguientes pasos:
Paso 1: Calcular la derivada de la función.
Paso 2: Encontrar los puntos estacionarios con la derivada. Para esto, formamos una ecuación con la derivada y resolvemos para x. Es decir, tenemos $latex \frac{dy}{dx}=0$.
Paso 3: Determinar cuál de los puntos del paso 2 es el punto máximo. Para esto, usamos la segunda derivada.
Cuando tenemos un punto máximo, debemos tener $latex \frac{d^2y}{dx^2}<0$. Es decir, la segunda derivada en ese punto debe ser negativa.
Paso 4: Determinar la coordenada en y del punto máximo usando la coordenada en x del paso 3.
EJEMPLO
Encuentra las coordenadas del punto máximo de $latex f(x)=\frac{1}{3}x^3+x^2-3x$.
Solución
Paso 1: Empezamos encontrando la derivada de la función:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f'(x)=x^2+2x-3$
Paso 2: Ahora, usamos la derivada para encontrar los puntos estacionarios:
$latex x^2+2x-3=0$
$latex (x+3)(x-1)=0$
$latex x=-3~~$ o $latex ~~x=1$
Paso 3: Determinamos cuál es el punto máximo usando la segunda derivada:
$latex f^{\prime \prime}(x)=2x+2$
Cuando $latex x=-3$, tenemos $latex f^{\prime \prime}(x)<0$ y cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$. Entonces, el punto máximo está en $latex x=-3$.
Paso 4: La coordenada en y del punto máximo es:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f(x)=\frac{1}{3}(-3)^3+(-3)^2-3(-3)$
$latex y=9$
El punto máximo tiene las coordenadas (-3, 9).
Definición del punto mínimo de una función
Los puntos mínimos de funciones son los puntos en donde los valores de y de la función son los mínimos posibles. Esto significa que no hay otro punto en la función que tenga un valor de y menor que el punto mínimo.
Los puntos mínimos son puntos estacionarios de una función. En estos puntos, la pendiente de la recta tangente es igual a cero. Es decir, en un punto mínimo tenemos $latex \frac{dy}{dx}=0$.
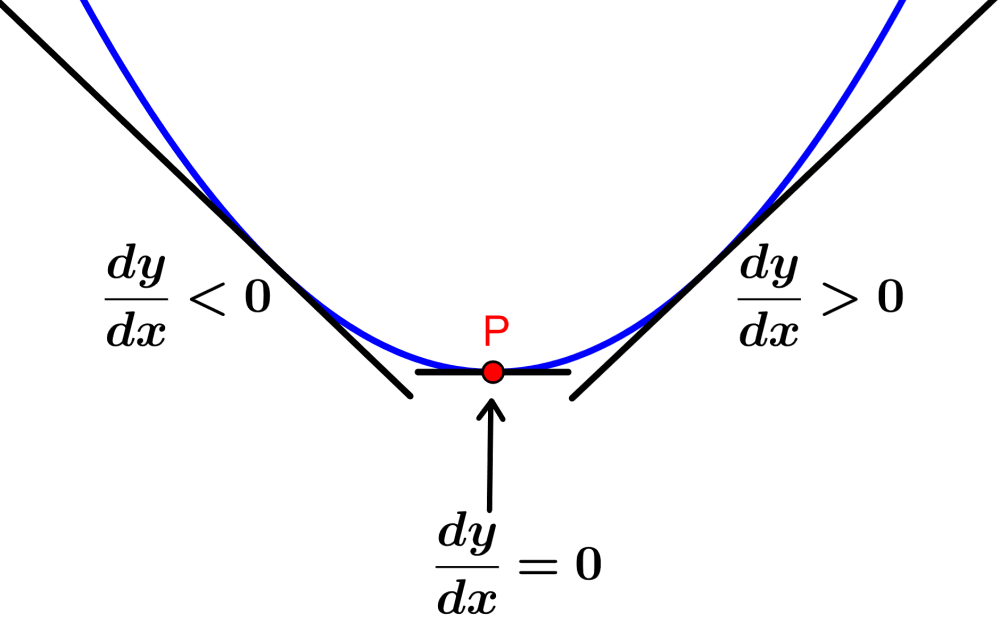
El siguiente diagrama es una representación gráfica de un punto mínimo en una función:
En la parte izquierda de un punto mínimo, la pendiente es negativa y en la parte derecha del punto mínimo, la pendiente es positiva. Es decir, la función decrece hasta que alcanza el punto mínimo y luego crece. Entonces, tenemos:
- En la parte izquierda de P: $latex \frac{dy}{dx}<0$
- En el punto P: $latex \frac{dy}{dx}=0$
- En la parte derecha de P: $latex \frac{dy}{dx}>0$
Dado que la pendiente (el valor de la derivada) va de negativa a positiva cerca al punto máximo, la segunda derivada de la función en un punto mínimo es positiva (la primera derivada crece).
Encontrar las coordenadas del punto mínimo de una función
Las coordenadas de un punto mínimo de una función son encontradas usando la derivada de la función. Recordamos que en estos puntos, la pendiente es igual a cero.
Entonces, formamos una ecuación con la derivada y encontramos sus raíces. Luego, usamos la segunda derivada para identificar a los puntos mínimos.
Si es que conocemos la función, podemos seguir los siguientes pasos para determinar su punto mínimo:
Paso 1: Obtener la derivada de la función.
Paso 2: Encontrar los puntos estacionarios usando la derivada. Entonces, formamos la ecuación $latex \frac{dy}{dx}=0$ y encontramos los valores de x.
Paso 3: Usar la segunda derivada para identificar al punto mínimo. Para que un punto estacionario sea un mínimo, debemos tener $latex \frac{d^2y}{dx^2}>0$.
Paso 4: Usar la coordenada en x del paso 3 para encontrar la coordenada en y del punto mínimo.
EJEMPLO
¿Cuáles son las coordenadas del punto mínimo de la función $latex f(x)=2x^3-6x$?
Solución
Paso 1: Empezamos encontrando la derivada de la función:
$latex f(x)=2x^3-6x$
$latex f'(x)=6x^2-6$
Paso 2: Determinamos los valores de x de la ecuación formada por la derivada:
$latex 6x^2-6=0$
$latex x=\sqrt{1}$
$latex x=\pm 1$
$latex x=1~~$ o $latex ~~x=-1$
Paso 3: Usamos la segunda derivada para determinar la naturaleza de los puntos estacionarios encontrados:
$latex f^{\prime \prime}(x)=12x$
Cuando $latex x=1$, tenemos $latex f^{\prime \prime}(x)>0$ y cuando $latex x=-1$, tenemos $latex f^{\prime \prime}(x)<0$. Esto significa que $latex x=1$ es el punto mínimo.
Paso 4: La coordenada en y del punto mínimo es:
$latex y=2x^3-6x$
$latex y=2(1)^3-6(1)$
$latex y=-4$
El punto mínimo de la función es (1, -4).
Definición de los puntos de inflexión de una función
Los puntos de inflexión de una función son puntos estacionarios en donde la pendiente es igual a cero. Es decir, en un punto de inflexión tenemos $latex \frac{dy}{dx}=0$.
La diferencia entre puntos de inflexión y puntos mínimos o máximos es que en los puntos de inflexión, la pendiente tiene el mismo signo en ambos lados del punto.
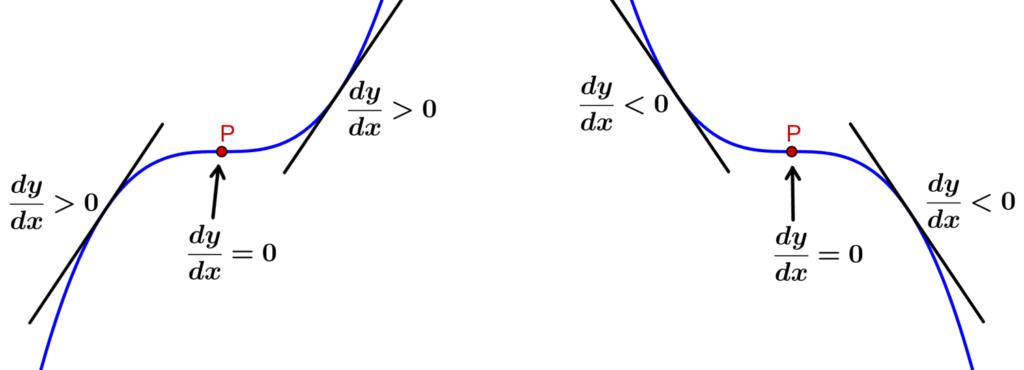
En el siguiente diagrama, podemos observar una representación gráfica de ambos casos de los puntos de inflexión de una función:
En el punto de inflexión de la izquierda, la función crece en ambos lados del punto de inflexión. Es decir, la pendiente es positiva en ambos lados, por lo que tenemos lo siguiente:
- En la parte izquierda de P: $latex \frac{dy}{dx}>0$
- En el punto P: $latex \frac{dy}{dx}=0$
- En la parte derecha de P: $latex \frac{dy}{dx}>0$
En el punto de inflexión de la derecha, la función decrece en ambos lados del punto de inflexión. Es decir, la pendiente es negativa en ambos lados, por lo que tenemos lo siguiente:
- En la parte izquierda de P: $latex \frac{dy}{dx}<0$
- En el punto P: $latex \frac{dy}{dx}=0$
- En la parte derecha de P: $latex \frac{dy}{dx}<0$
Encontrar las coordenadas de los puntos de inflexión de una función
Las coordenadas de los puntos de inflexión pueden ser encontradas usando la derivada de la función. Para esto consideramos que la pendiente en los puntos de inflexión es igual a cero.
Entonces, formamos una ecuación con la derivada de la función y encontramos los valores de x. Luego, usamos la segunda derivada para determinar cuál de los puntos es un punto de inflexión.
Si es que conocemos la función, podemos seguir los siguientes pasos para determinar las coordenadas de los puntos de inflexión:
Paso 1: Calcular la derivada de la función.
Paso 2: Usar la derivada para encontrar los puntos estacionarios de la función. Para esto, formamos la ecuación $latex \frac{dy}{dx}=0$ y determinamos los valores de x.
Paso 3: Usar la segunda derivada para identificar a los puntos de inflexión. Cuando tenemos un punto de inflexión, debemos tener $latex \frac{d^2y}{dx^2}=0$.
Sin embargo, los puntos máximos o puntos mínimos también podrían tener una segunda derivada que es igual a cero. Por esta razón, debemos verificar los signos a cada lado de los puntos de inflexión.
Para que un punto estacionario sea un punto de inflexión, la pendiente debe tener el mismo signo en ambos lados del punto. Es decir, la derivada debe tener el mismo signo.
Paso 4: Usar las coordenadas en x del paso 3 para encontrar las coordenadas en y de los puntos de inflexión.
EJEMPLO
Encuentra las coordendas del punto de inflexión de la función $latex f(x)=x^3-9x^2+27x-29$.
Solución
Paso 1: La siguiente es la derivada de la función:
$latex f(x)=x^3-9x^2+27x-29$
$latex f'(x)=3x^2-18x+27$
Paso 2: Usando la derivada, encontramos los puntos estacionarios:
$latex 3x^2-18x+27=0$
$latex 3(x^2-6x+9)=0$
$latex 3(x-3)(x-3)=0$
$latex x=3$
Paso 3: Usamos la segunda derivada para determinar si el punto es un punto de inflexión:
$latex f^{\prime \prime}(x)=6x-18$
Cuando $latex x=3$, tenemos $latex f^{\prime \prime}(x)=0$.
Además, cuando usamos $latex x=3.1$ (derecha del punto) y $late x=2.9$ (izquierda del punto) en la primera derivada, obtenemos dos valores positivos, por lo que confirmamos que es un punto de inflexión.
Paso 4: La coordenada en y del punto de inflexión es:
$latex y=x^3-9x^2+27x-29$
$latex y=(3)^3-9(3)^2+27(3)-29$
$latex y=-2$
Las coordenadas del punto de inflexión son (3, -2).
Véase también
¿Interesado en aprender más sobre derivadas y puntos estacionarios? Puedes mirar estas páginas: