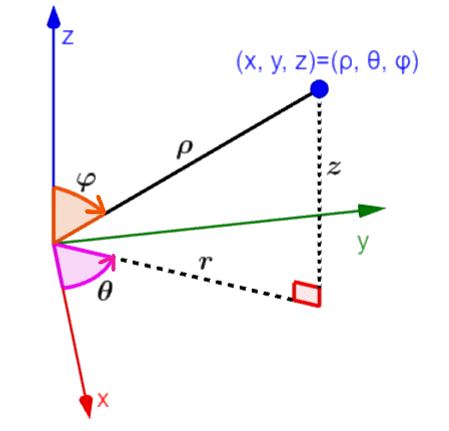
Las coordenadas esféricas tienen la forma (ρ, θ, φ), en donde, ρ es la distancia desde el origen hasta el punto, θ es el ángulo en el plano xy con respecto al eje x y φ es el ángulo con respecto al eje z. Estas coordenadas pueden ser transformadas a coordenadas cartesianas usando triángulos rectángulos y trigonometría. Usamos las funciones seno y coseno para encontrar los componentes verticales y horizontales y obtener expresiones para x, y, z en términos de ρ, θ, φ.
A continuación, derivaremos las fórmulas que podemos usar para transformar de coordenadas esféricas a cartesianas. Luego, aplicaremos estas fórmulas al resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas esféricas a cartesianas.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas esféricas a cartesianas.
¿Cómo transformar de coordenadas esféricas a coordenadas cartesianas?
Las coordenadas esféricas tienen la forma (ρ, θ, φ). En esta forma, ρ representa a la distancia desde el origen hasta el punto, θ representa al ángulo en el plano xy con respecto al eje x y φ representa al ángulo con respecto al eje z. Por otra parte, las coordenadas cartesianas tridimensionales tienen la forma $latex (x, y, z)$.
Para transformar de coordenadas esféricas a cartesianas, tenemos que usar triángulos rectángulos y trigonometría. Para facilitar la derivación de las fórmulas de transformación, podemos empezar transformando de coordenadas esféricas a cilíndricas y luego, podremos transformar de coordenadas cilíndricas a cartesianas.
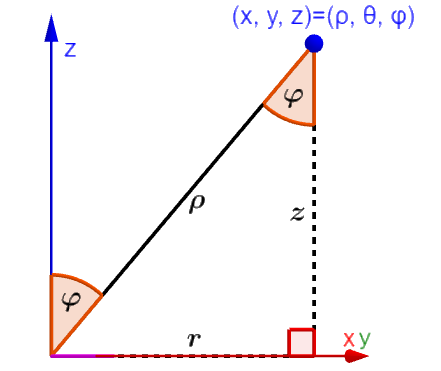
Entonces, usamos el siguiente diagrama:
Sabemos que el ángulo entre el eje z y ρ es igual a φ. Usando un poco de geometría, también sabemos que φ es el ángulo entre ρ y el lado vertical del triángulo. Luego, usando trigonometría, tenemos:
$latex z=\rho \cos(\phi)$
$latex r=\rho \sin(\phi)$
También tenemos $latex \theta= \theta$. Estas son las fórmulas que nos permiten convertir de coordenadas esféricas a cilíndricas. Ahora, podemos usar las fórmulas de transformación de coordenadas cilíndricas a cartesianas:
$latex x=r~\cos(\theta)$
$latex y=r~\sin(\theta)$
$latex z=z~~~~~$
Usando estos dos conjuntos de ecuaciones, podemos obtener las fórmulas de transformación de coordenadas esféricas a cartesianas:
| $latex x=\rho \sin(\phi)\cos(\theta)$ $latex y=\rho \sin(\phi)\sin(\theta)$ $latex z=\rho \cos(\phi)~~$ |
Ejercicios de coordenadas esféricas a cartesianas resueltos
Los siguientes ejercicios son resueltos usando las fórmulas de conversión de coordenadas esféricas a cartesianas. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Tenemos al punto $latex (10, \frac{\pi}{4}, \frac{\pi}{4})$ en coordenadas esféricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
Solución
Tenemos los valores $latex \rho=10,~\theta=\frac{\pi}{4},~\phi=\frac{\pi}{4}$. Ahora, usamos estos valores junto con las fórmulas vistas arriba para encontrar los valores de x y y. Entonces, el valor de x es:
$latex x=\rho~\sin(\phi)\cos(\theta)$
$latex x=10~\sin(\frac{\pi}{4})\cos(\frac{\pi}{4})$
$latex x=14.14$
El valor de y es:
$latex y=\rho~\sin(\phi)\sin(\theta)$
$latex y=10~\sin(\frac{\pi}{4})\sin(\frac{\pi}{4})$
$latex y=14.14$
El valor de z es:
$latex z=\rho~\cos(\phi)$
$latex z=10~\cos(\frac{\pi}{4})$
$latex z=7.07$
Las coordenadas cartesianas del punto son (14.14, 14.14, 7.07).
EJERCICIO 2
El punto $latex (5, \frac{3\pi}{2}, \frac{\pi}{3})$ está en coordenadas esféricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
Solución
Podemos reconocer los valores $latex \rho=5,~\theta=\frac{3\pi}{2},~\phi=\frac{\pi}{3}$. Encontramos los valores de x, y y z usando las fórmulas vistas arriba. Empezamos con el valor de x:
$latex x=\rho~\sin(\phi)\cos(\theta)$
$latex x=5~\sin(\frac{\pi}{3})\cos(\frac{3\pi}{2})$
$latex x=0$
El valor de y es:
$latex y=\rho~\sin(\phi)\sin(\theta)$
$latex y=5~\sin(\frac{\pi}{3})\sin(\frac{3\pi}{2})$
$latex y=-4.33$
El valor de z es:
$latex z=\rho~\cos(\phi)$
$latex z=10~\cos(\frac{\pi}{3})$
$latex z=5$
Las coordenadas cartesianas del punto son (0, -4.33, 5).
EJERCICIO 3
Si es que tenemos las coordenadas esféricas $latex (8, \frac{2\pi}{5}, \frac{\pi}{5})$, ¿cuál es su equivalencia en coordenadas cartesianas?
Solución
Podemos observar los valores $latex \rho=8,~\theta=\frac{2\pi}{5},~\phi=\frac{\pi}{5}$. Encontramos los valores de x, y, z al usar las fórmulas de transformación. Entonces, el valor de x es:
$latex x=\rho~\sin(\phi)\cos(\theta)$
$latex x=8~\sin(\frac{\pi}{5})\cos(\frac{2\pi}{5})$
$latex x=1.45$
El componente y es:
$latex y=\rho~\sin(\phi)\sin(\theta)$
$latex y=8~\sin(\frac{\pi}{5})\sin(\frac{2\pi}{5})$
$latex y=4.47$
El componente z es:
$latex z=\rho~\cos(\phi)$
$latex z=8~\cos(\frac{\pi}{5})$
$latex z=6.47$
Las coordenadas cartesianas del punto son (1.45, 4.47, 6.47).
EJERCICIO 4
Tenemos al punto $latex (10, \frac{\pi}{4}, \frac{4\pi}{3})$ en coordenadas esféricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
Solución
Reconocemos los valores $latex \rho=10,~\theta=\frac{\pi}{4},~\phi=\frac{4\pi}{3}$. Usando estos valores junto con las fórmulas de transformación, vamos a encontrar los componentes x, y y z. Entonces, el componente x es:
$latex x=\rho~\sin(\phi)\cos(\theta)$
$latex x=10~\sin(\frac{4\pi}{3})\cos(\frac{\pi}{4})$
$latex x=-6.12$
El componente y es:
$latex y=\rho~\sin(\phi)\sin(\theta)$
$latex y=10~\sin(\frac{4\pi}{3})\sin(\frac{\pi}{4})$
$latex y=-6.12$
El componente z es:
$latex z=\rho~\cos(\phi)$
$latex z=10~\cos(\frac{4\pi}{3})$
$latex z=-5$
Las coordenadas cartesianas del punto son (-6.12, -6.12, -5).
Ejercicios de coordenadas esféricas a cartesianas para resolver
Usa las fórmulas de transformación vistas arriba para resolver los siguientes ejercicios y convertir las coordenadas esféricas a coordenadas cartesianas. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre coordenadas esféricas y otros sistemas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
