Los sistemas de coordenadas pueden ser definidos como formas de ubicar a puntos en el espacio. En el espacio tridimensional, el sistema de coordenadas cartesianas tiene la forma (x, y, z). Sin embargo, este sistema no siempre es el más conveniente, por lo que tenemos sistemas de coordenadas alternativos. Uno de estos sistemas es el sistema de coordenadas cilíndricas.
Las coordenadas cilíndricas son consideradas como una extensión de las coordenadas polares hacia la tercera dimensión. La forma general de las coordenadas cilíndricas es (r, θ, z), en donde, r es la distancia desde el origen hasta el punto en el plano xy, θ es el ángulo formado con respecto al eje x y z es el mismo componente z que en coordenadas cartesianas.
¿Qué son las coordenadas cilíndricas?
Las coordenadas cilíndricas son definidas como un sistema de coordenadas tridimensional alterno al sistema cartesiano. Las coordenadas cilíndricas son escritas en la forma (r, θ, z), en donde, r representa a la distancia desde el origen hasta el punto en el plano xy, θ representa al ángulo formado con respecto al eje x y z es el componente z, el cual es el mismo que en coordenadas cartesianas.
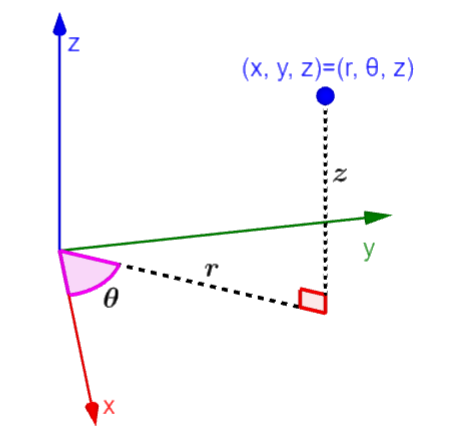
Este sistema de coordenadas es usado principalmente para graficar figuras con forma cilíndrica como tubos o tanques. Esto resulta principalmente conveniente en el cálculo, ya que dependiendo en las ecuaciones dadas, encontrar sus derivadas o integrales puede resultar más fácil.
Ejemplos de coordenadas cilíndricas
Para ubicar a un punto en las coordenadas cilíndricas, empezamos ubicándolo en el plano xy al medir la distancia desde el origen y medir el ángulo desde el eje x. Luego, añadimos el componente z. En la siguiente gráfica, podemos mirar al punto $latex (3, \frac{\pi}{3}, 4)$.
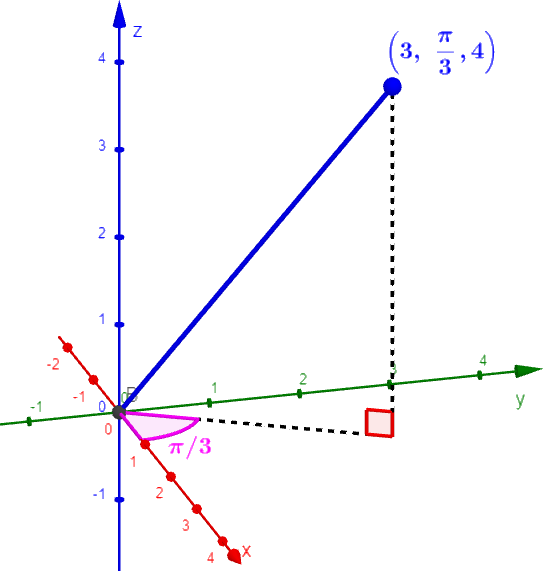
Una característica de las coordenadas cilíndricas es que podemos describir a un punto usando varias coordenadas. Es decir, existe un número infinito de coordenadas para cada punto. Esto se debe a que el ángulo θ puede ser escrito de formas diferentes.
Si es que sumamos o restamos 2π, obtenemos un ángulo equivalente. Por ejemplo, los ángulos $latex \frac{\pi}{2}$, $latex \frac{5\pi}{2}$ y $latex -\frac{3\pi}{2}$ son los mismos.
Fórmulas de conversión de cilíndricas a cartesianas
Usamos el siguiente diagrama para derivar las fórmulas de conversión de coordenadas cilíndricas a coordenadas cartesianas:
Podemos mirar que la coordenada z es la misma en ambos sistemas. Entonces, solo tenemos que encontrar los valores de x y y en términos de r y θ. Podemos usar la función coseno para encontrar al componente x y la función seno para encontrar al componente y. Entonces, tenemos:
| $latex x=r~\cos(\theta)$ $latex y=r~\sin(\theta)$ $latex z=z$ |
EJERCICIO 1
Si es que tenemos las coordenadas cilíndricas $latex (3, \frac{\pi}{4}, 4)$, ¿cuál es su equivalente en coordenadas cartesianas?
Solución
Podemos reconocer los valores $latex r=3, ~\theta=\frac{\pi}{4}$. Usamos a las fórmulas vistas arriba junto con estos valores:
$latex x=3 \cos(\frac{\pi}{4})$
$latex x=2.1$
$latex y=3 \sin(\frac{\pi}{4})$
$latex y=2.1$
Las coordenadas cartesianas son (2.1, 2.1, 4).
EJERCICIO 2
Tenemos las coordenadas cilíndricas $latex (10, \frac{7\pi}{4}, 5)$. ¿Cuál es su equivalente en coordenadas cartesianas?
Solución
Tenemos los valores $latex r=10, ~\theta=\frac{7\pi}{4}$. Usando estos valores, encontramos los valores de x y y:
$latex x=10 \cos(\frac{7\pi}{4})$
$latex x=7.07$
$latex y=10 \sin(\frac{7\pi}{4})$
$latex y=-7.07$
Las coordenadas cartesianas son (7.07, -7.07, 5).
Fórmulas de conversión de cartesianas a cilíndricas
Para derivar las fórmulas de conversión de coordenadas cartesianas a cilíndricas, vamos a usar el mismo diagrama:
El valor de r es encontrado usando el teorema de Pitágoras con los componentes x y y. Entonces, tenemos:
$latex {{r}^2}={{x}^2}+{{y}^2}$
| $latex r=\sqrt{{{x}^2}+{{y}^2}}$ |
El ángulo θ puede ser encontrado usando la tangente inversa. Sabemos que la tangente es igual al lado opuesto dividido por el lado adyacente. En el diagrama, vemos que el lado opuesto es y y el lado adycente es x. Entonces, tenemos:
| $latex \theta=\tan^{-1}(\frac{y}{x})$ |
Algo que debemos tener en cuenta con este ángulo es que a veces, el valor dado por la calculadora es incorrecto. Esto se debe a que las salidas de la tangente inversa van desde $latex -\frac{\pi}{2}$ hasta $latex \frac{\pi}{2}$ y esto no cubre los cuatro cuadrantes.
Podemos corregir esto al sumar 180° o π cuando el punto está en el segundo y tercer cuadrantes y sumar 360° o 2π cuando el punto está en el cuarto cuadrante. Cuando el punto está en el primer cuadrante, el valor dado por la calculadora es el correcto.
EJERCICIO 1
El punto (4, 6, 7) está en coordenadas cartesianas. ¿Cuál es su equivalente en coordenadas cilíndricas?
Solución
Tenemos los valores $latex x=4,~y=6$. Podemos encontrar a r y θ usando las fórmulas dadas arriba. Entonces, el valor de r es:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{4}^2}+{{6}^2}}$
$latex r=\sqrt{16+36}$
$latex r=\sqrt{52}$
$latex r=7.2$
El ángulo θ es:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{6}{4})$
$latex \theta=0.98$ rad
Tanto el componente x como el componente y son positivos, por lo que el punto está en el primer cuadrante y el ángulo obtenido es el correcto.
Las coordenadas del punto son (7.2, 0.98 rad, 7).
EJERCICIO 2
Tenemos al punto (-3, -6, 5) en coordenadas cartesianas. ¿Cuál es su equivalencia en coordenadas cilíndricas?
Solución
Reconocemos a $latex x=-3,~y=-6$. Usamos las fórmulas de arriba para encontrar a r y θ:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-3)}^2}+{{(-6)}^2}}$
$latex r=\sqrt{9+36}$
$latex r=\sqrt{47}$
$latex r=6.9$
El ángulo θ es:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-6}{-3})$
$latex \theta=1.11$ rad
Tanto el componente x como el componente y son negativos, por lo que el punto está en el tercer cuadrante y tenemos que sumar π para obtener el ángulo correcto. Entonces, el ángulo correcto es $latex \theta=1.11+\pi=4.25$ rad.
Las coordenadas del punto son (6.9, 4.25 rad, 5).
Véase también
¿Interesado en aprender más sobre coordenadas cilíndricas y otros sistemas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
