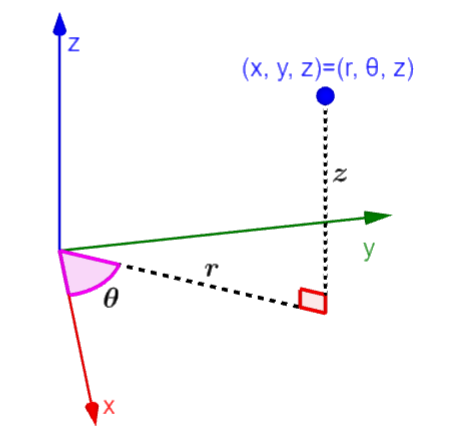
Las coordenadas cilíndricas tienen la forma (r, θ, z), en donde, r es la distancia en el plano xy, θ es el ángulo formado con respecto al eje x y z es el componente vertical en el eje z. Similar a las coordenadas polares, podemos relacionar a las coordenadas cilíndricas con las coordenadas cartesianas al usar un triángulo rectángulo y trigonometría. Usamos al coseno para encontrar el componente x y al seno para encontrar al componente y. El componente en z se mantiene igual.
A continuación, veremos las fórmulas que podemos aplicar para transformar de coordenadas cilíndricas a cartesianas. Luego, usaremos estas fórmulas para resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas cilíndricas a cartesianas.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas cilíndricas a cartesianas.
¿Cómo transformar de coordenadas cilíndricas a coordenadas cartesianas?
Las coordenadas cartesianas tridimensionales están representadas en la forma $latex (x, y, z)$. Un sistema de coordenadas tridimensional alterno es el sistema de coordenadas cilíndricas. El sistema de coordenadas cilíndricas es una extensión en tres dimensiones del sistema de coordenadas polares.
Las coordenadas polares son extendidas en la tercera dimensión similar a como extendimos a las coordenadas cartesianas, es decir, simplemente añadimos a z como la tercera dimensión.
Entonces, las coordenadas cilíndricas tienen la forma (r, θ, z), en donde, r es la distancia desde el origen hasta la posición del punto en el plano xy, θ es el ángulo con respecto al eje x y z es la coordenada en el eje z.
Las transformaciones para x y y son las mismas a las usadas en las coordenadas polares. Para encontrar el componente x, usamos la función coseno y para encontrar el componente y, usamos la función seno.
Además, el componente z de las coordenadas cilíndricas es el igual al componente en z de las coordenadas cartesianas.
| $latex x=r~\cos(\theta)$ $latex y=r~\sin(\theta)$ $latex z=z~~~~~$ |
Ejercicios de coordenadas cilíndricas a cartesianas resueltos
Las fórmulas de transformación de coordenadas cilíndricas a coordenadas cartesianas son usadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Tenemos al punto (3, 30°, 6) en coordenadas cilíndricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
Solución
Empezamos reconociendo los valores $latex r=3,~\theta=30^{\circ},~z=6$. Usando estos valores y las fórmulas vistas arriba, tenemos que encontrar los valores de x y y. Entonces, el valor de x es:
$latex x=r~\cos(\theta)$
$latex x=3~\cos(30)$
$latex x=2.6$
El valor de y es:
$latex y=r~\sin(\theta)$
$latex y=3~\sin(30)$
$latex y=1.5$
Sabemos que el componente z permanece igual, por lo que las coordenadas del punto son (2.6, 1.5, 6).
EJERCICIO 2
¿Cuáles son las coordenadas cartesianas del punto (5, 45°, -4)?
Solución
Usamos los valores $latex r=5,~\theta=45^{\circ},~z=-4$ para encontrar los diferentes componentes de las coordenadas cartesianas. Empezamos con el valor de x:
$latex x=r~\cos(\theta)$
$latex x=5~\cos(45)$
$latex x=3.54$
Ahora, encontramos el valor de y:
$latex y=r~\sin(\theta)$
$latex y=5~\sin(45)$
$latex y=3.54$
El componente z es el mismo, por lo que las coordenadas cartesianas del punto son (3.54, 3.54, -4).
EJERCICIO 3
Tenemos a un punto con las coordenadas cilíndricas (6, 120°, 7). ¿Cuáles son las coordenadas cartesianas de este punto?
Solución
Encontramos las coordenadas cartesianas usando los valores $latex r=6,~\theta=120^{\circ},~z=7$ junto con las fórmulas vistas arriba. Entonces, el valor de x es:
$latex x=r~\cos(\theta)$
$latex x=6~\cos(120)$
$latex x=-3$
El valor de y es:
$latex y=r~\sin(\theta)$
$latex y=6~\sin(120)$
$latex y=5.2$
El componente z es el mismo, por lo que las coordenadas del punto son (-3, 5.2, 7).
EJERCICIO 4
Tenemos al punto (12, 90°, 8) en coordenadas cilíndricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
Solución
Tenemos los valores $latex r=12,~\theta=90^{\circ},~z=8$. Encontramos el valor de x de la siguiente manera:
$latex x=r~\cos(\theta)$
$latex x=12~\cos(90)$
$latex x=0$
Encontramos el valor de y de la siguiente manera:
$latex y=r~\sin(\theta)$
$latex y=12~\sin(90)$
$latex y=12$
Sabemos que el componente z permanece igual, por lo que las coordenadas del punto son (0, 12, 8).
Ejercicios de coordenadas cilíndricas a cartesianas para resolver
Usa las fórmulas vistas arriba para resolver los siguientes ejercicios y transformar las coordenadas cilíndricas a coordenadas cartesianas. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre coordenadas cilíndricas y otros sistemas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
