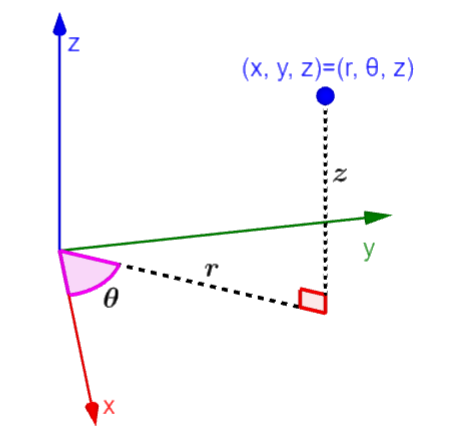
Las coordenadas cilíndricas son un sistema de coordenadas tridimensional alterno al sistema de coordenadas cartesianas. Las coordenadas cilíndricas tienen la forma (r, θ, z), en donde, r es la distancia en el plano xy, θ es el ángulo de r con respecto al eje x y z es el componente en el eje z. Este sistema de coordenadas puede presentar ventajas con respecto al sistema cartesiano al momento de graficar figuras cilíndricas como tubos o tanques.
A continuación, conoceremos las fórmulas que podemos usar para transformar de coordenadas cartesianas a coordenadas cilíndricas. Luego, veremos algunos ejercicios de práctica en los que aplicaremos estas fórmulas.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas cartesianas a cilíndricas.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas cartesianas a cilíndricas.
¿Cómo transformar de coordenadas cartesianas a coordenadas cilíndricas?
Las coordenadas cilíndricas pueden resultar más convenientes cuando queremos graficar cilindros, tubos o figuras semejantes. Este sistema de coordenadas es usado en cálculo, ya que permite usar un sistema referencial más fácil para figuras cilíndricas y encontrar derivadas o integrales resulta más fácil.
El sistema de coordenadas cilíndricas tiene la forma $latex (r, \theta, z)$, en donde, r es la distancia desde el origen hasta la ubicación del punto en el plano xy y θ es el ángulo formado por la línea y el eje x.
Este sistema de coordenadas es considerado como una extensión hacia la tercera dimensión del sistema de coordenadas polares. Comparando a estas coordenadas con las coordenadas cartesianas, $latex (x,y,z)$, vemos que el componente de la tercera dimensión, z, es el mismo.
Podemos usar a un triángulo rectángulo y al teorema de Pitágoras para encontrar el valor de r en términos de x y y. Las coordenadas x y y forman los catetos del triángulo y r forma la hipotenusa. Entonces, tenemos la relación:
$latex {{r}^2}={{x}^2}+{{y}^2}$
| $latex r=\sqrt{{{x}^2}+{{y}^2}}$ |
Para encontrar el ángulo θ, usamos a la función tangente inversa. La función tangente de un ángulo en un triángulo es igual al lado opuesto dividido por el lado adyacente. En este caso, el lado opuesto es igual a la coordenada y y el lado adycente es la coordenada x. Entonces, tenemos:
| $latex \theta=\tan^{-1}(\frac{y}{x})$ |
Una complicación a la hora de encontrar el ángulo θ es que muchas veces, la calculadora no retorna el valor correcto del ángulo. Esto se debe a que el rango de la función tangente inversa va desde $latex -\frac{\pi}{2}$ hasta $latex \frac{\pi}{2}$ y esto no cubre los cuatro cuadrantes del plano cartesiano.
Podemos resolver esto usando la siguiente tabla para corregir los ángulos:
| Cuadrante | Valor de $latex {{\tan}^{-1}}$ |
| I | La calculadora da el valor correcto |
| II | Debemos sumar 180° al valor de la calculadora |
| III | Debemos sumar 180° al valor de la calculadora |
| IV | Debemos sumar 360° al valor de la calculadora |
→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas
Ejercicios de coordenadas cartesianas a cilíndricas resueltos
Las fórmulas de transformación de coordenadas cartesianas a cilíndricas son aplicadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos las coordenadas cartesianas (2, 2, 5), ¿cuál es la equivalencia en coordenadas cilíndricas?
Solución
Sabemos que tenemos $latex x=2,~y=2,~z=5$. Entonces, tenemos que encontrar a r, θ y z para formar las coordenadas cilíndricas. Encontramos a r, usando la siguiente ecuación:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{2}^2}+{{2}^2}}$
$latex r=\sqrt{4+4}$
$latex r=\sqrt{8}$
Encontramos a θ, usando la siguiente fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{2}{2})$
$latex \theta={{\tan}^{-1}}(1)$
$latex \theta=45$° $latex =\frac{\pi}{4}$
El componente en z es el mismo, por lo que las coordenadas cilíndricas son $latex (\sqrt{8}, \frac{\pi}{4}, 5)$.
EJERCICIO 2
¿A qué es igual el punto (-3, 6, 3) en coordenadas cilíndricas?
Solución
Tenemos los valores $latex x=-3,~y=6,~z=3$. Tenemos que encontrar a r, θ y z, usando estos valores. Empezamos con r:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-3)}^2}+{{6}^2}}$
$latex r=\sqrt{9+36}$
$latex r=\sqrt{45}$
$latex r=3\sqrt{5}$
Ahora, encontramos al ángulo θ, usando la siguiente fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{6}{-3})$
$latex \theta={{\tan}^{-1}}(-2)$
$latex \theta=-63.4$°
Sin embargo, observamos que el punto está ubicado en el segundo cuadrante, ya que el componente en x es negativo y el componente en y es positivo. Entonces, tenemos que sumar 180° al valor obtenido. Eso significa que el ángulo es $latex \theta=-63.4+180=116.6$°.
El componente en z es el mismo. Entonces, el punto en coordenadas cilíndricas es $latex (3\sqrt{5}, 116.6^{\circ}, 3)$.
EJERCICIO 3
Si es que tenemos al punto (-4, -1, -3) en coordenadas cartesianas, ¿cuál es su equivalencia en coordenadas cilíndricas?
Solución
Podemos reconocer a los valores $latex x=-4,~y=-1,~z=-3$. Para encontrar a este punto en coordenadas cilíndricas, tenemos que encontrar a r, θ y z. Podemos encontrar a r, usando la siguiente ecuación:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-4)}^2}+{{(-1)}^2}}$
$latex r=\sqrt{16+1}$
$latex r=\sqrt{17}$
Ahora, encontramos al ángulo θ, usando la siguiente fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-1}{-4})$
$latex \theta=14$°
En este caso, el punto se encuentra en el tercer cuadrante, ya que tanto el componente x como el componente y son negativos. Entonces, tenemos que sumar 180° al ángulo obtenido para encontrar el ángulo correcto. El ángulo correcto es $latex \theta=14+180=194$°.
Teniendo en cuenta que el componente z es el mismo, las coordenadas cilíndricas son $latex (\sqrt{17}, 194^{\circ}, -3)$.
EJERCICIO 4
Determina la equivalencia en coordenadas cilíndricas del punto (2, -6, 4).
Solución
Reconocemos a los valores $latex x=2,~y=-6,~z=4$. Usamos a estos valores para encontrar a r, θ y z y formar las coordenadas cilíndricas. Encontramos a r, usando la siguiente ecuación:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{2}^2}+{{(-6)}^2}}$
$latex r=\sqrt{4+36}$
$latex r=\sqrt{40}$
$latex r=2\sqrt{10}$
El ángulo θ, es encontrado de la siguiente forma:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-6}{2})$
$latex \theta={{\tan}^{-1}}(-3)$
$latex \theta=-71.6$°
Observamos que el punto se encuentra en el cuarto cuadrante, ya que el componente en x es positivo y el componente en y es negativo.
Entonces, tenemos que sumar 360° al ángulo dado por la calculadora para encontrar el valor correcto. El ángulo correcto es $latex \theta=-71.6+360=288.4$°.
Mantenemos al componente z, por lo que las coordenadas cilíndricas son $latex (2\sqrt{10}, 288.4^{\circ}, 4)$.
Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas
Ejercicios de coordenadas cartesianas a cilíndricas para resolver
Pon en práctica lo aprendido sobre la transformación de coordenadas cartesianas a cilíndricas al resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que seleccionaste la correcta.
→ Explora más ejercicios de práctica
Véase también
¿Interesado en aprender más sobre coordenadas cilíndricas y otros sistemas? Mira estas páginas:
