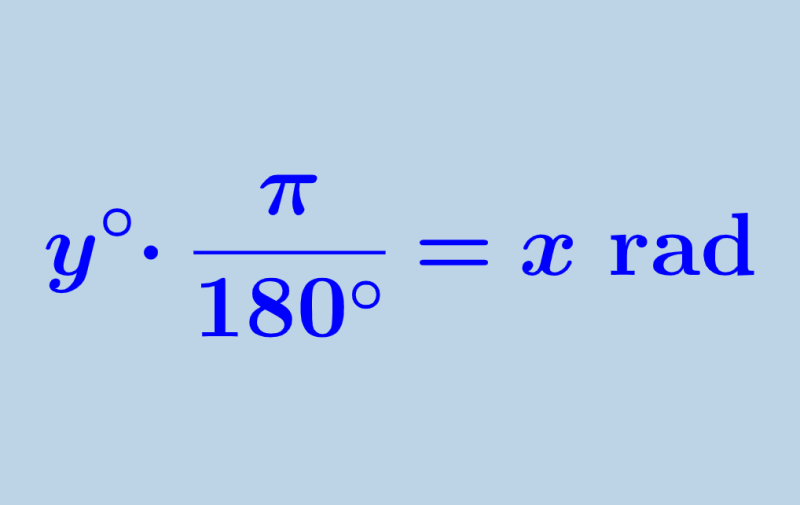Los grados y los radianes son los dos tipos de unidades más comunes para medir ángulos. Cada una de estas unidades es conveniente en diferentes situaciones. Los grados son usados en geometría ya que nos permiten medir a un ángulo e indicar una dirección. Sin embargo, técnicamente hablando, los ángulos no son números y sólo podemos realizar cálculos matemáticos con números. Por esta razón, los radianes son más convenientes a la hora de trabajar en cálculo u otros temas matemáticos avanzados. Para convertir de grados a radianes, tenemos que multiplicar por π y dividir por 180°.
A continuación, aprenderemos sobre el proceso usado para convertir de grados a radianes con ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de grados a radianes con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de grados a radianes con ejercicios.
¿Cómo convertir de grados a radianes?
Podemos convertir de grados a radianes al multiplicar al ángulo dado por π y dividir por 180°. Esto significa que tenemos la siguiente fórmula:
| $latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad |
Aquí, y representa al ángulo en grados y x es la respuesta en radianes.
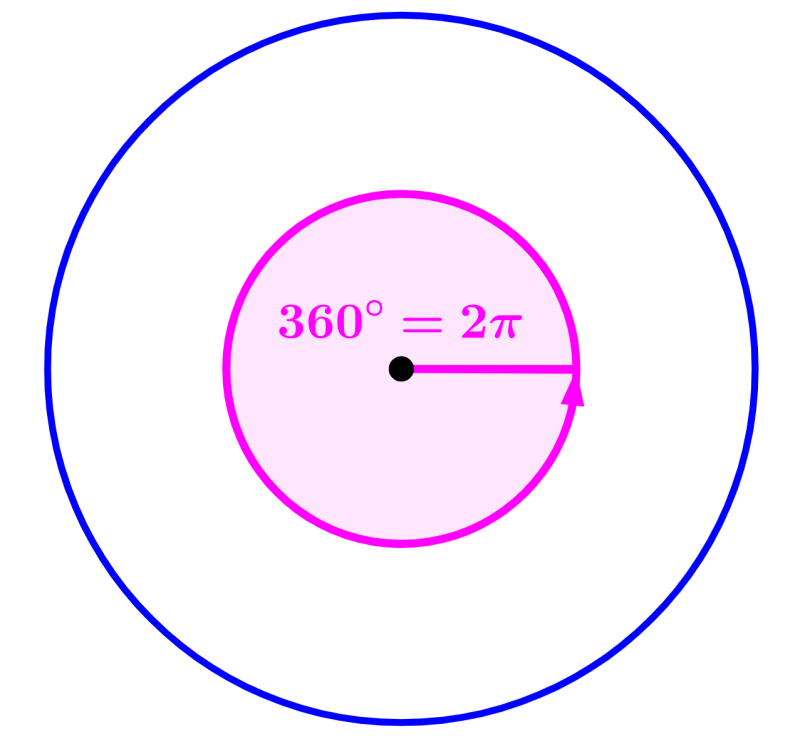
Podemos derivar a esta fórmula al considerar que tenemos 360° en un círculo completo. Además, también sabemos que una vuelta completa es equivalente a 2π radianes. Entonces, podemos formar la relación 2π = 360°.
Ahora, podemos simplificar a esta relación al dividir por dos a ambos lados. Al dividir por dos, obtenemos π = 180°. Esta es la relación usada para convertir de grados a radianes.
Ejercicios de transformación de grados a radianes resueltos
La fórmula de transformación de grados a radianes es usada para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuántos radianes es igual a 240°?
Solución
Usamos la fórmula de transformación con el valor dado. Entonces, tenemos:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 240^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{4\pi}{3}$ rad
Entonces, 240° es equivalente a $latex \frac{4\pi}{3}$ radianes.
EJERCICIO 2
Convierte 200° a radianes.
Solución
Usamos el ángulo dado en la fórmula vista arriba para obtener:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 200^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{10\pi}{9}$ rad
Entonces, 200° es igual a $latex \frac{10\pi}{9}$ radianes.
EJERCICIO 3
¿Cuántos radianes es igual a 86°?
Solución
Reemplazamos el ángulo dado en la fórmula de transformación para obtener:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 86^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{43\pi}{90}$ rad
Entonces, el ángulo 86° es equivalente a $latex \frac{43\pi}{90}$ radianes o 1.5 radianes.
EJERCICIO 4
Convierte 110° a radianes.
Solución
Reemplazamos al valor dado en la fórmula de transformación y tenemos:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 110^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{11\pi}{18}$ rad
Entonces, 110° es equivalente a $latex \frac{11\pi}{18}$ radianes o 1.92 radianes.
EJERCICIO 5
¿Cuánto es 68° en radianes?
Solución
Usamos la fórmula de transformación con el valor dado. Entonces, tenemos:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 68^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{17\pi}{45}$ rad
Entonces, 68° es equivalente a $latex \frac{17\pi}{45}$ radianes o 1.19 radianes.
Ejercicios de transformación de grados a radianes para resolver
Resuelve los siguientes ejercicios de práctica usando la fórmula de transformación de grados a radianes. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre grados y radianes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
