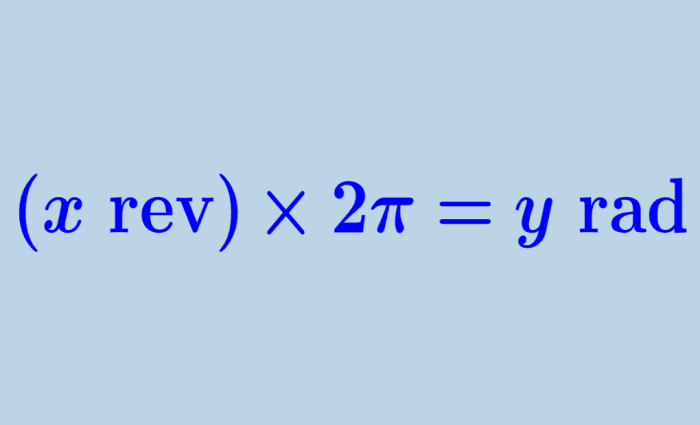Los radianes son una manera de medir a los ángulos. Los radianes son principalmente usados cuando queremos realizar operaciones matemáticas avanzadas como el cálculo diferencial o integral. Esto se debe a que el radián tiene una relación con el radio del círculo. Por otra parte, las revoluciones son una forma para considerar a una vuelta completa alrededor de un círculo. Esto significa que una revolución es igual a 2π. Entonces, para convertir revoluciones a radianes, multiplicamos a las revoluciones por 2π.
A continuación, aplicaremos el proceso de transformación de revoluciones a radianes al resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender a convertir de revoluciones a radianes con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender a convertir de revoluciones a radianes con ejercicios.
¿Cómo convertir de revoluciones a radianes?
Para convertir de revoluciones a radianes , tenemos que multiplicar al número de revoluciones por 2π y obtendremos al ángulo en radianes que corresponde al número de revoluciones dado. Entonces, tenemos la siguiente fórmula:
| $latex (x \text{ rev}) \times 2\pi=y$ rad |
en donde, x representa al número de revoluciones y y es la respuesta en radianes.
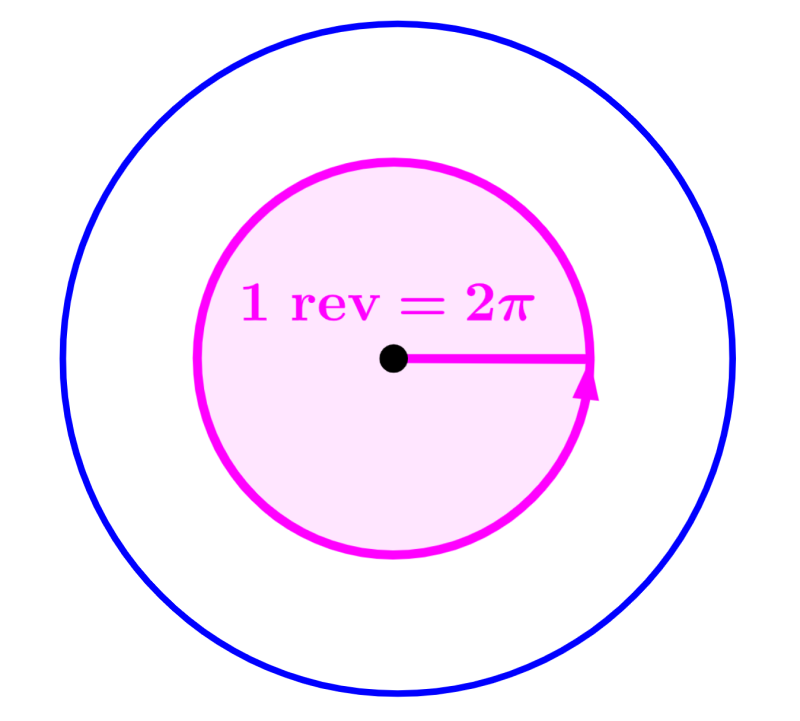
Esta fórmula es derivada considerando a un círculo. Si es que damos una vuelta completa a un círculo, tenemos un ángulo de 2π radianes. Además, por definición, una revolución equivale a una vuelta completa al círculo. Esto significa que podemos formar la relación 1 rev = 2π.
Entonces, teniendo cualquier número de revoluciones, simplemente tenemos que multiplicar por 2π para encontrar los radianes equivalentes.
Ejercicios de transformación de revoluciones a radianes resueltos
Los siguientes ejercicios de práctica son resueltos usando la fórmula de transformación de revoluciones a radianes dada arriba. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos 3 revoluciones, ¿cuántos radianes tenemos?
Solución
Reemplazamos al valor dado en la fórmula de transformación, para obtener:
$latex (x\text{ rev})\times 2\pi=y \text{ rad}$
$latex (3\text{ rev})\times 2\pi=6 \pi\text{ rad}$
Entonces, 3 revoluciones equivale a 6π radianes.
EJERCICIO 2
Convierte 6 revoluciones a radianes.
Solución
Usando $latex x=6$ que es el número de revoluciones, tenemos:
$latex (x\text{ rev})\times 2\pi=y \text{ rad}$
$latex (6\text{ rev})\times 2\pi=12 \pi\text{ rad}$
Entonces, 6 revoluciones equivale a 12π radianes.
EJERCICIO 3
¿Cuántos radianes es igual a 2.5 revoluciones?
Solución
En este caso, tenemos un número fraccionario, pero la fórmula a usar es la misma. Usamos el valor en la fórmula y tenemos:
$latex (x\text{ rev})\times 2\pi=y \text{ rad}$
$latex (2.5\text{ rev})\times 2\pi=5 \pi\text{ rad}$
Entonces, 2.5 revoluciones es igual a 5π radianes.
EJERCICIO 4
Si es que tenemos 3.8 revoluciones, ¿cuántos radianes tenemos?
Solución
Usamos el valor $latex x=3.8$ en la fórmula de transformación y resolvemos:
$latex (x\text{ rev})\times 2\pi=y \text{ rad}$
$latex (3.8\text{ rev})\times 2\pi=7.6 \pi\text{ rad}$
Entonces, 3.8 revoluciones equivale a 7.6 π radianes o 23.9 radianes.
EJERCICIO 5
¿Cuántos radianes es igual a 6.5 revoluciones?
Solución
Podemos usar la fórmula con el valor $latex x=6.5$ para obtener:
$latex (x\text{ rev})\times 2\pi=y \text{ rad}$
$latex (6.5\text{ rev})\times 2\pi=13 \pi\text{ rad}$
Entonces, 6.5 revoluciones equivale a 13π radianes.
Ejercicios de transformación de revoluciones a radianes para resolver
Practica el uso de la fórmula de transformación de revoluciones a radianes al resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre grados y radianes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
