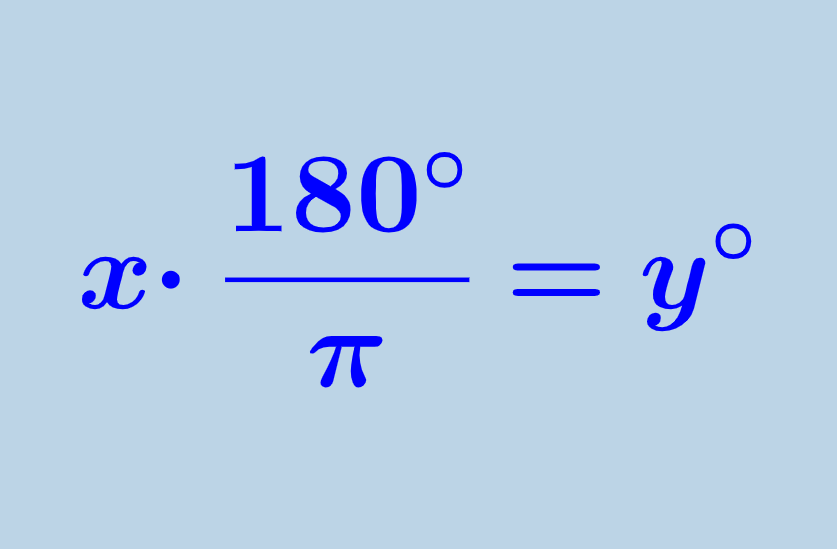Los radianes y los grados son tipos de unidades para medir ángulos. Existen otros tipos de unidades, pero los radianes y los grados son los más usados. Cada una de estas unidades tiene su respectiva aplicación. Los radianes son principalmente usados en el cálculo diferencial e integral. Por otra parte, los grados son usados en la geometría y permiten expresar direccionalidad y el tamaño del ángulo. Podemos convertir radianes a grados al multiplicar por 180° y dividir por π.
A continuación, veremos algunos ejercicios en donde aprenderemos el proceso usado para convertir de radianes a grados.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de radianes a grados con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de radianes a grados con ejercicios.
¿Cómo convertir de radianes a grados?
Para convertir de radianes a grados, tenemos que multiplicar a los radianes por 180° y dividir por π. Entonces, tenemos la fórmula:
| $latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$ |
en donde, x es el ángulo en radianes y y es el ángulo en grados.
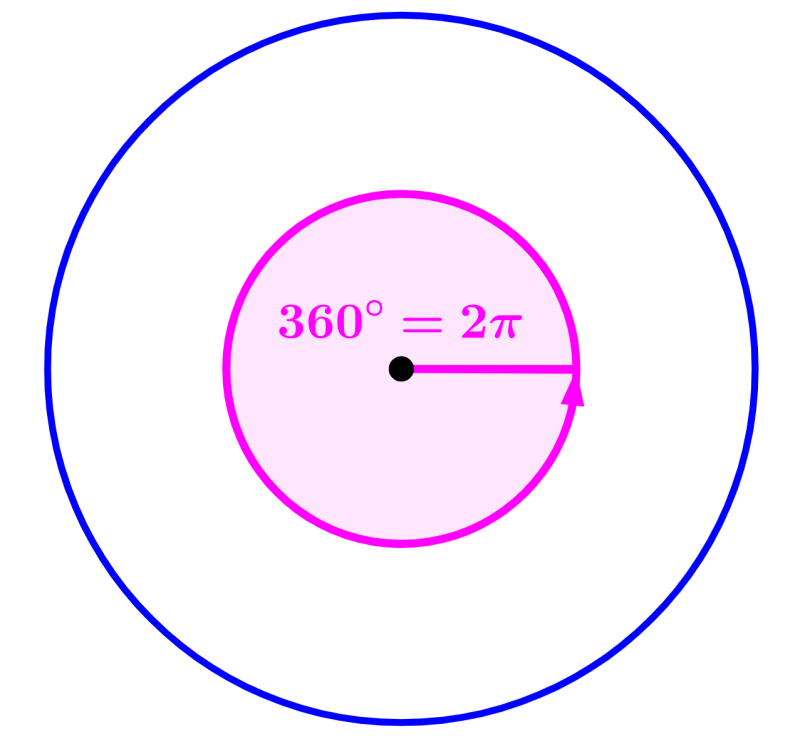
Esta fórmula es derivada del hecho que tenemos 360° en un círculo. Cuando expresamos al ángulo en radianes, sabemos que tenemos 2π radianes en un círculo. Esto significa que 2π = 360°. Podemos dividir por dos a esta expresión para obtener π = 180°. Entonces, esta es la relación que usamos para convertir de radianes a grados.
Ejercicios de transformación de radianes a grados resueltos
Los siguientes ejercicios son resueltos usando la fórmula de transformación de radianes a grados vista arriba. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Convierte $latex \frac{4\pi}{5}$ radianes a grados.
Solución
Simplemente usamos los radianes dados en la fórmula de conversión para obtener los grados:
$latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$
$latex \frac{4\pi}{5}\cdot \frac{180^{\circ}}{\pi}=144^{\circ}$
Entonces, $latex \frac{4\pi}{5}$ radianes es equivalente a 144°.
EJERCICIO 2
¿Cuántos grados es igual a $latex \frac{2\pi}{9}$ radianes?
Solución
Reemplazamos al valor dado en la fórmula de conversión. Entonces, tenemos:
$latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$
$latex \frac{2\pi}{9}\cdot \frac{180^{\circ}}{\pi}=40^{\circ}$
Entonces, $latex \frac{2\pi}{9}$ radianes es equivalente a 40°.
EJERCICIO 3
¿Cuántos grados es igual a $latex \frac{12\pi}{7}$ radianes?
Solución
Usamos la fórmula de conversión de radianes a grados junto con el valor dado para obtener los grados:
$latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$
$latex \frac{12\pi}{7}\cdot \frac{180^{\circ}}{\pi}=308.6^{\circ}$
Entonces, 308.6° es igual a $latex \frac{12\pi}{7}$ radianes.
EJERCICIO 4
Convierte 2.5 radianes a grados.
Solución
En este caso, simplemente tenemos $latex x=2.5$. Entonces, tenemos:
$latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$
$latex 2.5\cdot \frac{180^{\circ}}{\pi}=143.2^{\circ}$
Entonces, 2.5 radianes es equivalente a 143.2°.
EJERCICIO 5
¿Cuánto es 3.2 radianes en grados?
Solución
Tenemos el valor $latex x=3.2$. Usando a este valor en la fórmula, tenemos:
$latex x\cdot \frac{180^{\circ}}{\pi}=y^{\circ}$
$latex 3.2\cdot \frac{180^{\circ}}{\pi}=183.3^{\circ}$
Entonces, 3.2 radianes es equivalente a 183.3°.
Ejercicios de transformación de radianes a grados para resolver
Usa lo aprendido sobre transformación de radianes a grados y la fórmula derivada para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar tu respuesta.
Véase también
¿Interesado en aprender más sobre grados y radianes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
