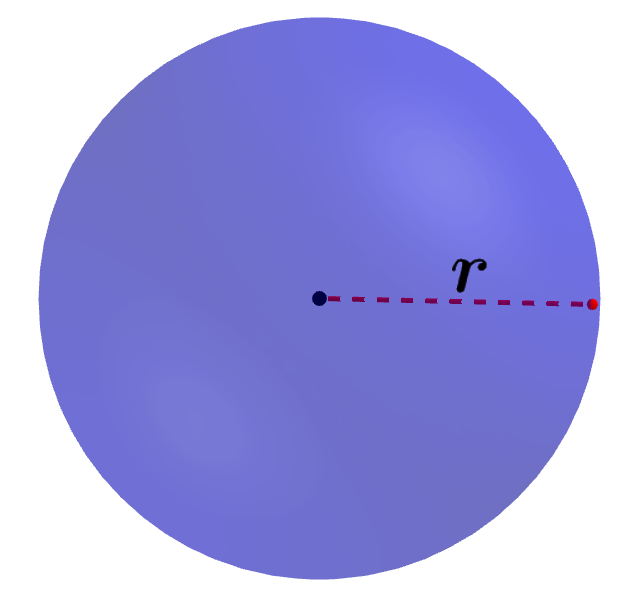
El área superficial de una esfera es representa a la región cubierta por su superficie exterior. Por otro lado, el volumen representa el espacio tridimensional ocupado por la figura. Podemos calcular el área superficial de una esfera usando la fórmula A=4πr² y podemos calcular su volumen usando la fórmula V=(4/3) πr³, en donde, r es el radio de la esfera.
A continuación, aprenderemos todo lo relacionado con el área y el volumen de una esfera. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de una esfera.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de una esfera.
¿Cómo calcular el área superficial de una esfera?
Podemos calcular el área superficial de una esfera al multiplicar por 4 al producto de pi y el cuadrado del radio de la esfera. Entonces, la fórmula del área superficial de una esfera está dada por:
| $latex A_{s}=4\pi{{r}^2}$ |
en donde, $latex A_{s}$ representa al área superficial de la esfera y r representa a la longitud del radio.
Calcular el área superficial de una esfera usando el diámetro
Si es que conocemos la longitud del diámetro, podemos calcular su área superficial usando dos métodos principales. El primer método consiste en dividir la longitud del diámetro por 2 y así usar la fórmula de estándar del área superficial de una esfera.
El segundo método consiste en encontrar una fórmula para el área superficial de una esfera en términos del diámetro. Entonces, reemplazando la expresión r=d/2 en la fórmula del área superficial, tenemos:
$latex A_{s}=4\pi{{r}^2}$
$latex A_{s}=4\pi(\frac{d}{2})^2$
$latex A_{s}=4\pi(\frac{d^2}{4})$
| $latex A_{s}=\pi{{d}^2}$ |
¿Cómo calcular el volumen de una esfera?
Podemos calcular el volumen de una esfera usando la siguiente fórmula:
| $latex V=\frac{4}{3}\pi {{r}^3}$ |
en donde, r es la longitud del radio de la esfera.
La fórmula del volumen de una esfera puede ser demostrada usando cálculo integral.
Calcular el volumen de una esfera usando el diámetro
Para calcular el volumen de una esfera usando su diámetro, podemos usar dos métodos diferentes. El primer método consiste en dividir al diámetro por 2 para obtener el radio y usar la fórmula estándar del volumen de una esfera.
El segundo método consiste en obtener una fórmula para el volumen de una esfera en términos del diámetro. Podemos lograr esto al sustituir la expresión r=d/2 en la fórmula del volumen. Entonces, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(\frac{d}{2})}^3}$
$latex V=\frac{4}{3}\pi (\frac{{{d}^3}}{8})$
$latex V=\frac{4}{24}\pi {{d}^3}$
| $latex V=\frac{1}{6}\pi {{d}^3}$ |
en donde, d es la longitud del diámetro.
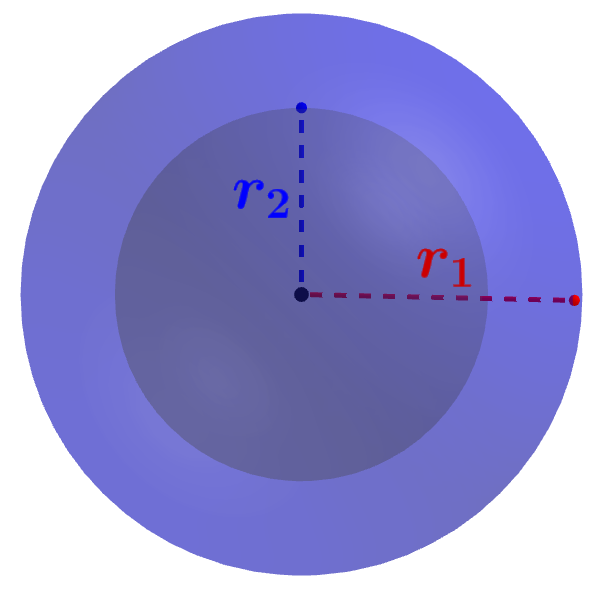
Calcular el volumen de una esfera hueca
Podemos calcular el volumen de una esfera hueca al sustraer el volumen de la parte hueca del volumen total de la esfera. Entonces, si es que usamos a $latex r_{1}$ para representar al radio de la esfera completa y a $latex r_{2}$ para representar al radio interno, es decir, el radio de la parte hueca, tenemos:
$latex V=\frac{4}{3}\pi {{r_{1}}^3}-\frac{4}{3}\pi {{r_{2}}^3}$
Simplificando, podemos obtener la siguiente fórmula:
| $latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$ |
Área superficial y volumen de una esfera – Ejercicios resueltos
Las fórmulas del área superficial y del volumen de una esfera son usadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Calcula el área superficial de una esfera que tiene un radio de 4 mm.
Solución
Usando la fórmula del área superficial con la longitud $latex r=4$, tenemos:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(4)}^2}$
$latex A_{s}=4\pi (16)$
$latex A_{s}=201.1$
El área superficial es igual a 201.1 mm².
EJERCICIO 2
Encuentra el volumen de una esfera que tiene un radio de 3 cm.
Solución
Usando la fórmula del volumen en términos del radio con $latex r=3$, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(3)}^3}$
$latex V=\frac{4}{3}\pi (27)$
$latex V=113.1$
El volumen es igual a 113.1 cm³.
EJERCICIO 3
¿Cuál es el área superficial de una esfera que tiene un radio de 5 cm?
Solución
Usamos el radio $latex r=5$ en la fórmula del área superficial. Entonces, tenemos:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(5)}^2}$
$latex A_{s}=4\pi (25)$
$latex A_{s}=314.2$
El área superficial es igual a 314.2 cm².
EJERCICIO 4
¿Cuál es el volumen de una esfera que tiene un radio de 4 mm?
Solución
Usando la fórmula del volumen en términos del radio con la longitud $latex r=4$, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(4)}^3}$
$latex V=\frac{4}{3}\pi (64)$
$latex V=268.1$
El volumen es igual a 268.1 mm³.
EJERCICIO 5
Encuentra el área superficial de una esfera que tiene un diámetro de 12 cm.
Solución
Dado que tenemos la longitud del diámetro, podemos dividirlo por 2 para obtener el radio. Entonces, usamos la fórmula del área superficial con la longitud $latex r=6$:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(6)}^2}$
$latex A_{s}=4\pi (36)$
$latex A_{s}=452.4$
El área superficial es igual a 452.4 cm².
EJERCICIO 6
Encuentra el volumen de una esfera que tiene un diámetro de 5 m.
Solución
Dado que tenemos el diámetro de la esfera, podemos dividirlo 2 para obtener el radio. Esto significa que el radio es igual a $latex r=2.5$. Entonces, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(2.5)}^3}$
$latex V=\frac{4}{3}\pi (6.25)$
$latex V=26.2$
El volumen es igual a 26.2 m³.
EJERCICIO 7
¿Cuál es el radio de una esfera que tiene un área superficial de 200 cm²?
Solución
En este caso, conocemos el área superficial y queremos encontrar la longitud del radio. Entonces, usaremos la fórmula del área superficial y resolvemos para r:
$latex A_{s}=4\pi {{r}^2}$
$latex 200=4\pi {{r}^2}$
$latex 50=\pi {{r}^2}$
$latex 15.92={{r}^2}$
$latex r=3.99$
La longitud del radio es 3.99 cm.
EJERCICIO 8
Encuentra volumen de una esfera hueca que tiene un radio externo de 6 cm y un radio interno de 4 cm.
Solución
La esfera hueca tiene los radios $latex r_{1}=6$ y $latex r_{2}=4$. Entonces, podemos usar la fórmula del volumen de una esfera hueca con estos radios:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(6)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (216-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=636.7$
El volumen es igual a 636.7 cm³.
EJERCICIO 9
Encuentra el radio de una esfera que tiene un área superficial de 460 m².
Solución
Vamos a usar la fórmula del área superficial y resolvemos para r:
$latex A_{s}=4\pi {{r}^2}$
$latex 460=4\pi {{r}^2}$
$latex 115=\pi {{r}^2}$
$latex 36.6={{r}^2}$
$latex r=6.05$
La longitud del radio es 6.05 m.
EJERCICIO 10
¿Cuál es el volumen de una esfera hueca tiene un radio externo de 5 mm y un radio interno de 4 mm?
Solución
Los radios de la esfera hueca son $latex r_{1}=5$ y $latex r_{2}=4$. Entonces, tenemos:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(5)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (125-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=255.5$
El volumen es igual a 255.5 mm³.
Área superficial y volumen de una esfera – Ejercicios para resolver
Usa las fórmulas del área superficial y del volumen de una esfera para resolver los siguientes ejercicios. Haz clic en «Verificar» para comprobar si es que tu respuesta es la correcta.
Véase también
¿Interesado en aprender más sobre área y volumen de figuras geométricas? Puedes mirar estas páginas: