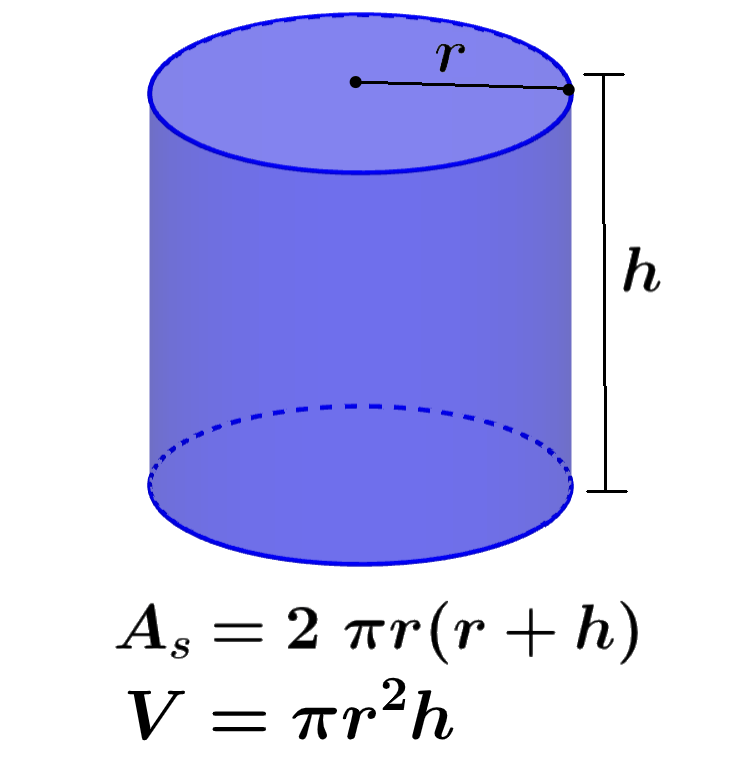
El área superficial de un cilindro representa la suma de las áreas de sus caras y es una medida bidimensional. Por otro lado, el volumen es una medida del espacio tridimensional ocupado por el cilindro. Podemos calcular el área superficial de un cilindro usando la fórmula A=2πr(r+h) y podemos calcular su volumen usando la fórmula V=πr²h, en donde r es el radio y h es la altura del cilindro.
A continuación, aprenderemos sobre el área superficial y el volumen de un cilindro. Conoceremos las diferentes fórmulas que podemos usar para calcular estas medidas y las aplicaremos para resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de un cilindro.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de un cilindro.
¿Cómo calcular el área superficial de un cilindro?
Para calcular el área superficial de un cilindro, tenemos que sumar las áreas de todas las caras del cilindro. Entonces, podemos usar las siguientes fórmulas:
| $latex A_{s}=2\pi {{r}^2}+2\pi r h$ o $latex A_{s}=2\pi r(r+h)$ |
en donde, r es la longitud del radio y h es la altura del cilindro.
Demostración de la fórmula del área superficial de un cilindro
Para demostrar la fórmula del área superficial de un cilindro, consideramos que el área total de un cilindro está compuesta de las siguientes partes:
- Área de las bases
- Área de la superficie curvada
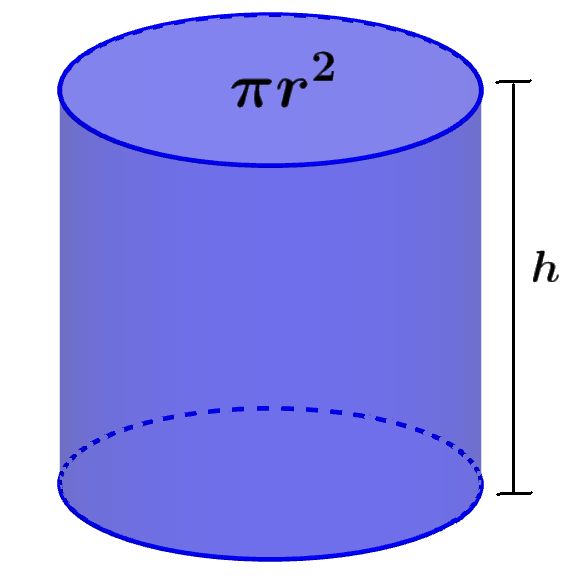
Área de las bases del cilindro
El cilindro tiene dos bases circulares, por lo que podemos calcular su área usando la fórmula del área de un círculo. Dado que tenemos dos bases circulares, multiplicamos a la fórmula del área de un círculo por 2:
$latex \text{Área}_{\text{bases}}=2\pi{{r}^2}$
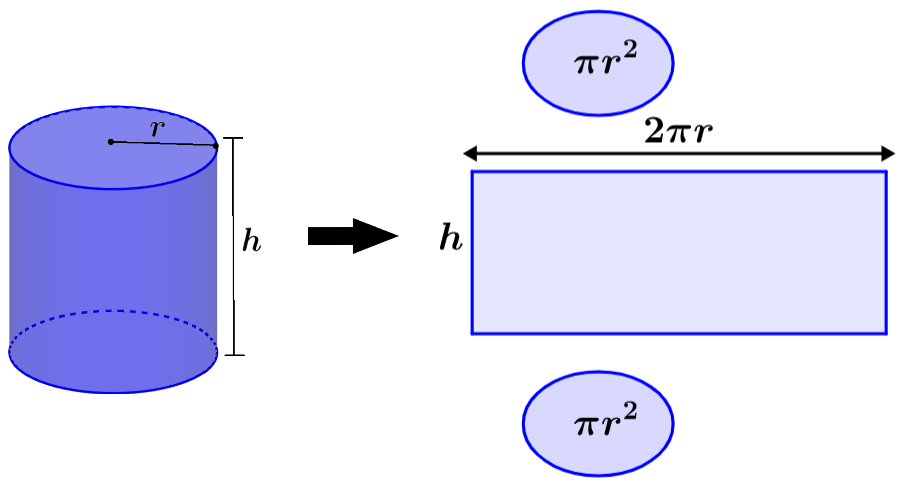
Área de la superficie curva del cilindro
El área de la superficie lateral puede ser calculada usando el diagrama mostrado abajo. Si es que estiramos esta superficie, formamos un rectángulo con una altura de h y una base que es igual a la circunferencia de las bases circulares, es decir, 2πr.
Entonces, podemos encontrar esta área con la siguiente fórmula:
$latex \text{Área}_{\text{lateral}}=2\pi r h$
Área superficial total del cilindro
Para encontrar el área superficial total del cilindro, tenemos que sumar el área de las bases circulares y el área de la superficie lateral:
$latex A_{s}=2\pi {{r}^2}+2\pi r h$
o
$latex A_{s}=2\pi r(r+h)$
¿Cómo calcular el volumen de un cilindro?
Podemos calcular el volumen de un cilindro al multiplicar al área de la base por su altura:
Volumen = Base × Altura
Dado que las bases de un cilindro son circulares, el área de la base es igual a πr², en donde r es el radio. Entonces, la fórmula del volumen de un cilindro es:
| $latex V=\pi {{r}^2}\times h$ |
en donde, r es la longitud del radio del cilindro y h es la longitud de su altura.
Calcular el volumen de un cilindro usando el diámetro
Para calcular el volumen de un cilindro usando el diámetro, podemos usar dos métodos diferentes. El primer método consiste en dividir el diámetro por 2 para obtener la longitud del radio y aplicar la fórmula del volumen indicada arriba.
Alternativamente, podemos encontrar una fórmula para el volumen de un cilindro en términos del diámetro al sustituir la expresión r=d/2:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(\frac{d}{2})}^2}\times h$
$latex V=\pi \frac{{{d}^2}}{4}\times h$
| $latex V= \frac{\pi{{d}^2}}{4}\times h$ |
en donde, d es la longitud del diámetro.
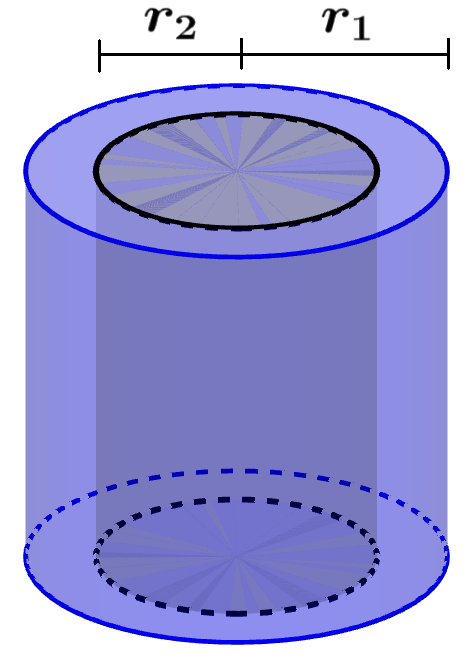
¿Cómo calcular el volumen de un cilindro hueco?
Podemos calcular el volumen de un cilindro hueco al restar el volumen de la parte hueca del volumen total del cilindro. Esto puede ser logrado usando la siguiente fórmula:
| $latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$ |
en donde, $latex r_{1}$ es el radio del cilindro, $latex r_{2}$ es el radio de la parte hueca y h es la altura del cilindro.
Esta fórmula es equivalente a calcular el volumen de un cilindro entero y luego extraer el volumen del cilindro interno que fue removido.
Área y volumen de un cilindro – Ejercicios resueltos
Las fórmulas del área superficial y del volumen de un cilindro son usadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra el área superficial de un cilindro que tiene un radio de 5 cm y una altura de 8 cm.
Solución
Tenemos las siguientes longitudes:
- Radio, $latex r=5$
- Altura, $latex h=8$
Usando estas longitudes en la fórmula del área superficial, tenemos:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (5)(5+8)$
$latex A_{s}=2\pi (5)(13)$
$latex A_{s}=408.4$
El área superficial es igual a 408.4 cm².
EJERCICIO 2
Encuentra el volumen de un cilindro que tiene un radio de 5 mm y una altura de 10 mm.
Solución
Tenemos lo siguiente:
- Radio, $latex r=5$
- Altura, $latex h=10$
Aplicando la fórmula del volumen con las longitudes dadas, tenemos:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(5)}^2}\times 10$
$latex V=\pi (25)\times 10$
$latex V=785.4$
El volumen es igual a 785.4 mm³.
EJERCICIO 3
¿Cuál es el área superficial de un cilindro que tiene una altura de 7 m y un radio de 6 m?
Solución
Tenemos lo siguiente:
- Radio, $latex r=6$
- Altura, $latex h=7$
Usando estos valores en la fórmula del área superficial, tenemos:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (6)(6+7)$
$latex A_{s}=2\pi (6)(13)$
$latex A_{s}=490.1$
El área superficial es igual a 490.1 m².
EJERCICIO 4
Calcula el volumen de un cilindro que tiene un radio de 6 cm y una altura de 8 cm.
Solución
Tenemos las siguientes longitudes:
- Radio, $latex r=6$
- Altura, $latex h=8$
Usando la fórmula del volumen con estas longitudes, tenemos:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(6)}^2}\times 8$
$latex V=\pi (36)\times 8$
$latex V=904.8$
El volumen es igual a 904.8 cm³.
EJERCICIO 5
¿Cuál es el área superficial de un cilindro que tiene una altura de 12 mm y un radio de 8 mm?
Solución
Tenemos las siguientes longitudes:
- Radio, $latex r=8$
- Altura, $latex h=12$
Usando la fórmula del área superficial, tenemos:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (8)(8+12)$
$latex A_{s}=2\pi (8)(20)$
$latex A_{s}=1005.3$
El área superficial es igual a 1005.3 mm².
EJERCICIO 6
Encuentra el volumen de un cubo que tiene un diámetro de 8 cm y una altura de 12 cm.
Solución
Tenemos las siguientes longitudes:
- Diámetro, $latex d=8$
- Altura, $latex h=12$
En este caso, tenemos la longitud del diámetro, por lo que usamos la fórmula del volumen en términos del diámetro del cilindro:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(8)}^2}}{4})\times 12$
$latex V=\pi (\frac{64}{4})\times 12$
$latex V=\pi (16)\times 12$
$latex V=603.2$
El volumen es igual a 603.2 cm³.
EJERCICIO 7
¿Cuál es el área superficial de un cilindro que tiene un diámetro de 6 mm y una altura de 7 mm?
Solución
Dado que tenemos la longitud del diámetro simplemente podemos dividir al diámetro por 2 para obtener el radio del cilindro. Entonces, tenemos:
- Radio, $latex r=3$
- Altura, $latex h=7$
Aplicando la fórmula del área superficial, tenemos:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (3)(3+7)$
$latex A_{s}=2\pi (3)(10)$
$latex A_{s}=188.5$
El área superficial es igual a 188.5 mm².
EJERCICIO 8
Encuentra el volumen de un cilindro que tiene un diámetro de 12 m y una altura de 11 m.
Solución
Tenemos lo siguiente:
- Diámetro, $latex d=12$
- Altura, $latex h=11$
Usando la fórmula del volumen en términos del diámetro, tenemos:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(12)}^2}}{4})\times 11$
$latex V=\pi (\frac{144}{4})\times 11$
$latex V=\pi (36)\times 11$
$latex V=1244.1$
El volumen es igual a 1244.1 m³.
EJERCICIO 9
Encuentra el área superficial de un cilindro que tiene un diámetro de 12 cm y una altura de 13 cm.
Solución
Podemos dividir al diámetro por 2 para obtener el radio y tenemos:
- Radio, $latex r=6$
- Altura, $latex h=13$
Usando la fórmula del área superficial con los valores dados, tenemos:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (6)(6+13)$
$latex A_{s}=2\pi (6)(19)$
$latex A_{s}=716.3$
El área superficial es igual a 716.3 cm².
EJERCICIO 10
¿Cuál es el volumen de un cilindro hueco que tiene una altura de 15 mm, un radio interno de 5 mm y un radio externo de 6 mm?
Solución
Tenemos las siguiente longitudes:
- Altura, $latex h=15$
- Radio externo, $latex r_{1}=6$
- Radio interno, $latex r_{2}=5$
Usando la fórmula del volumen de un cilindro hueco, tenemos:
$latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$
$latex V=\pi (15)({{6}^2}-{{5}^2})$
$latex V=\pi (15)(36-25)$
$latex V=\pi (15)(11)$
$latex V=518.4$
El volumen es igual a 518.4 mm³.
Área y volumen de un cilindro – Ejercicios para resolver
Resuelve los siguientes ejercicios usando las diferentes fórmulas del área y del volumen de un cilindro. Puedes usar los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre área y volumen de figuras geométricas? Puedes mirar estas páginas: