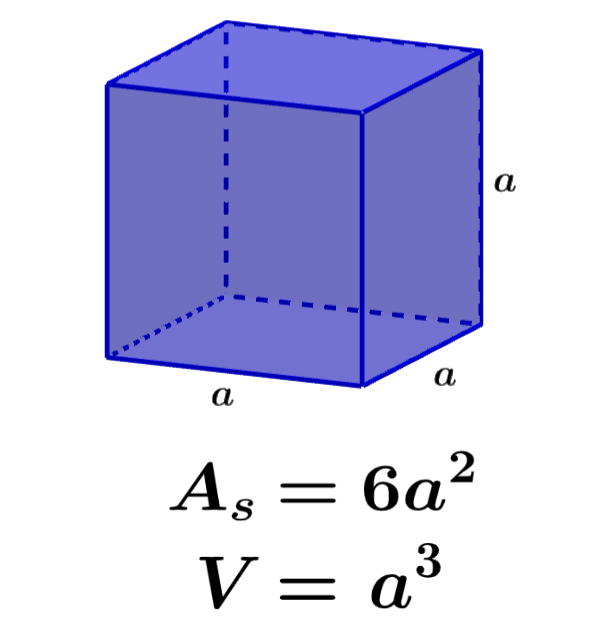
El área superficial de un cubo representa la suma de las áreas de todas las caras del cubo. Por otro lado, el volumen es una medida del espacio tridimensional ocupado por el cubo. Podemos calcular el área superficial de un cubo usando la fórmula A=6a² y podemos calcular su volumen usando la fórmula V=a³, en donde, a es la longitud de uno de los lados del cubo.
A continuación, aprenderemos todo lo relacionado con el área superficial y el volumen de un cubo. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de un cubo.
GEOMETRÍA
Relevante para…
Aprender sobre el área superficial y el volumen de un cubo.
¿Cómo calcular el área superficial de un cubo?
Podemos calcular el área superficial de un cubo al sumar las áreas de sus seis caras. Sabemos que las caras de un cubo tiene una figura cuadrada. Entonces, podemos calcular el área de cada cara del cubo al elevar al cuadrado a la longitud de una de sus caras.
Usando la letra a para representar a uno de los lados del cubo, tenemos:
$latex \text{Área de una cara}={{a}^2}$
Al sumar las seis caras del cubo, tenemos:
$latex A_{s}={{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}$
| $latex A_{s}=6{{a}^2}$ |
en donde, $latex A_{s}$ representa al área superficial y a representa a la longitud de uno de los lados del cubo.
¿Cómo calcular el volumen de un cubo?
Dado que todos los lados de un cubo tienen la misma longitud, podemos calcular su área al elevar al cubo a la longitud de uno de sus lados. Entonces, tenemos lo siguiente:
Volumen = Longitud × Ancho × Altura
$latex V=a\times a \times a$
| $latex V={{a}^3}$ |
en donde, a es la longitud de uno de los lados del cubo.
Calcular el volumen de un cubo usando la diagonal
Si es que conocemos la longitud de una de las diagonales del cubo en vez de la longitud de sus lados, podemos usar la siguiente fórmula para calcular su volumen:
| $latex V=\sqrt{3} \times \frac{{{d}^3}}{9}$ |
en donde, d es la longitud de la diagonal de un cubo.
Área superficial y volumen de cubos – Ejercicios resueltos
Las fórmulas del área superficial y el volumen de un cubo son usadas para resolver los siguientes ejercicios. Cada ejercicio tiene su solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el área superficial de un cubo que tiene lados con una longitud de 5 mm.
Solución
Vamos a usar la fórmula del área superficial con la longitud $latex a=5$. Entonces, tenemos:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(5)}^2}$
$latex A_{s}=6(25)$
$latex A_{s}=150$
El área superficial es igual a 150 mm².
EJERCICIO 2
Encuentra el volumen de un cubo que tiene lados con una longitud de 5 cm.
Solución
Usando la fórmula del volumen con la longitud $latex a=5$, tenemos:
$latex V=a^3$
$latex V={{5}^3}$
$latex V=125$
El volumen es igual a 125 cm³.
EJERCICIO 3
Encuentra el área superficial de un cubo que tiene lados con una longitud de 10 m.
Solución
Usando la longitud $latex a=10$ en la fórmula del área superficial, tenemos:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(10)}^2}$
$latex A_{s}=6(100)$
$latex A_{s}=600$
El área superficial es igual a 600 m².
EJERCICIO 4
¿Cuál es el volumen de un cubo que tiene lados con una longitud de 10 mm?
Solución
Usando la fórmula del volumen con la longitud $latex a=10$, tenemos:
$latex V=a^3$
$latex V={{10}^3}$
$latex V=1000$
El volumen es igual a 1000 mm³.
EJERCICIO 5
Encuentra el área superficial de un cubo que tiene lados con una longitud de 12 cm.
Solución
Usando la longitud $latex a=12$ en la fórmula del área superficial, tenemos:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(12)}^2}$
$latex A_{s}=6(144)$
$latex A_{s}=864$
El área superficial es igual a 864 cm².
EJERCICIO 6
Encuentra la longitud de los lados de un cubo que tiene un volumen de 512 cm³.
Solución
En este caso, conocemos la medida del área y tenemos que encontrar la longitud de uno de los lados. Entonces, usamos la fórmula del volumen y resolvemos para a:
$latex V=a^3$
$latex 512={{a}^3}$
$latex a=8$
La longitud de uno de los lados es 8 cm.
EJERCICIO 7
Encuentra la longitud de los lados de un cubo que tiene un área superficial de 120 m².
Solución
En este caso, conocemos el área superficial y tenemos que encontrar la longitud de sus lados. Entonces, usamos la fórmula del área superficial y resolvemos para a:
$latex A_{s}=6{{a}^2}$
$latex 120=6{{a}^2}$
$latex 20={{a}^2}$
$latex a=4.47$
La longitud de los lados es 4.47 m.
EJERCICIO 8
Si es que un cubo tiene una diagonal de 5 mm, calcula su volumen.
Solución
Aquí, conocemos la longitud de la diagonal $latex d=5$, por lo que podemos la fórmula del volumen en términos de la diagonal con este valor:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{5}^3}}{9}$
$latex V=\sqrt{3}\times \frac{125}{9}$
$latex V=24.1$
El volumen es igual a 24.1 mm³.
EJERCICIO 9
¿Cuál es la longitud de los lados de un cubo que tiene un área superficial de 240 cm²?
Solución
Podemos usar la fórmula del área superficial con $latex A_{s}=240$ y resolver para a:
$latex A_{s}=6{{a}^2}$
$latex 240=6{{a}^2}$
$latex 40={{a}^2}$
$latex a=6.32$
La longitud de los lados es igual a 6.32 cm.
EJERCICIO 10
Encuentra el volumen de un cubo que tiene una diagonal de 10 m.
Solución
Usando la longitud $latex d=10$ en la fórmula del volumen en términos de la diagonal, tenemos:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{10}^3}}{9}$
$latex V=\sqrt{3}\times \frac{1000}{9}$
$latex V=192.5$
El volumen es igual a 192.5 m³.
Área superficial y volumen de un cubo – Ejercicios para resolver
Usa los siguientes ejercicios para practicar el uso de las fórmulas del área superficial y del volumen de cubos. Puedes usar los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre área y volumen de figuras geométricas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
