El área superficial de un prisma es una medida de la superficie bidimensional ocupada por el prisma. Por otro lado, el volumen es representa el espacio tridimensional ocupado por el prisma. Podemos calcular el área superficial de un prisma al sumar las áreas de todas sus caras y podemos calcular su volumen usando la fórmula V=Bh, en donde, B es el área de la base y h es la altura del prisma.
A continuación, aprenderemos todo lo relacionado con el área superficial y el volumen de un prisma. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial y el volumen de un prisma.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial y el volumen de un prisma.
¿Cómo calcular el área superficial de un prisma?
El área superficial de cualquier prisma puede ser calculado al sumar las áreas de todas las caras del prisma. Dependiendo del tipo de prisma que tengamos, tendremos un número diferente de caras.
En un prisma, tenemos dos bases que tienen las mismas dimensiones y la misma área. Además, tenemos varias caras laterales que pueden o no tener la misma área dependiendo de si las bases son regulares.
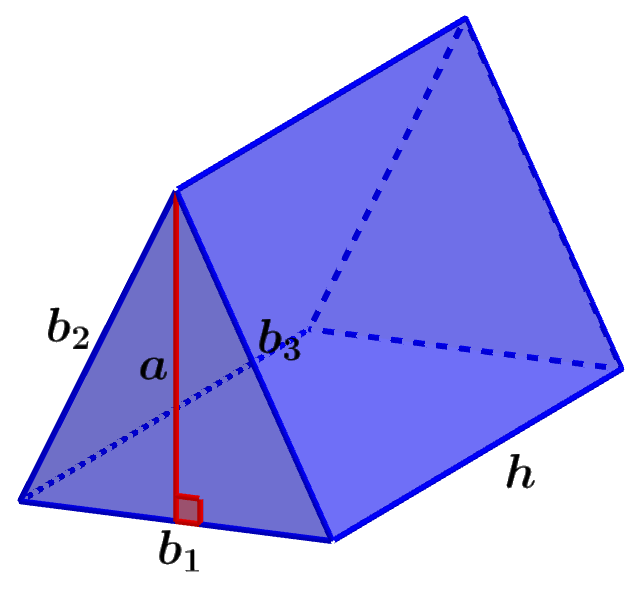
Por ejemplo, en el prisma triangular que podemos ver en el siguiente diagrama, podemos encontrar el área de las bases con la fórmula $latex \frac{1}{2}ab$, en donde a es la altura de la base triangular y b es la longitud de su base. Esto significa que el área de ambas caras triangulares es $latex ab$.
Además, el área de las caras laterales rectangulares es igual a la altura del prisma multiplicada por cada lado de la base triangular. Es decir, tenemos las áreas $latex b_{1}h$, $latex b_{2}h$ y $latex b_{3}h$. Entonces, el área superficial del prisma triangular es:
| $latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$ |
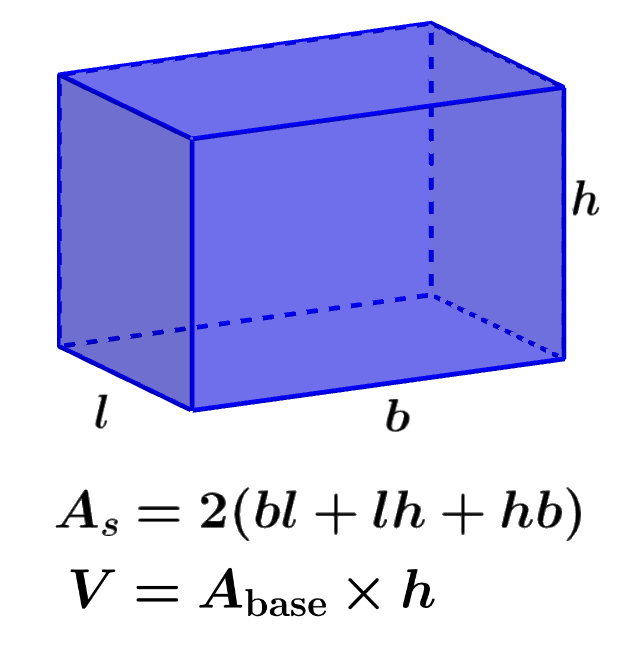
En el caso de un prisma rectangular, tenemos seis caras rectangulares. Generalmente, estos prismas tienen sus tres dimensiones con una longitud diferente, como se muestra en el siguiente diagrama.
Entonces, considerando que las caras paralelas en un prisma rectangular tienen la misma área, podemos obtener la siguiente fórmula para su área superficial:
| $latex A_{s}=2(bl+lh+hb)$ |
en donde,
- b es la longitud de la base del prisma
- l es la longitud del ancho del prisma
- h es la longitud de la altura del prisma
Estas ideas pueden ser aplicadas para calcular el área superficial de cualquier prisma.
¿Cómo calcular el volumen de un prisma?
El volumen de cualquier prisma puede ser calculado al multiplicar el área de su base por la altura del prisma. Entonces, podemos usar la siguiente fórmula:
| $latex V=A_{ base}\times h$ |
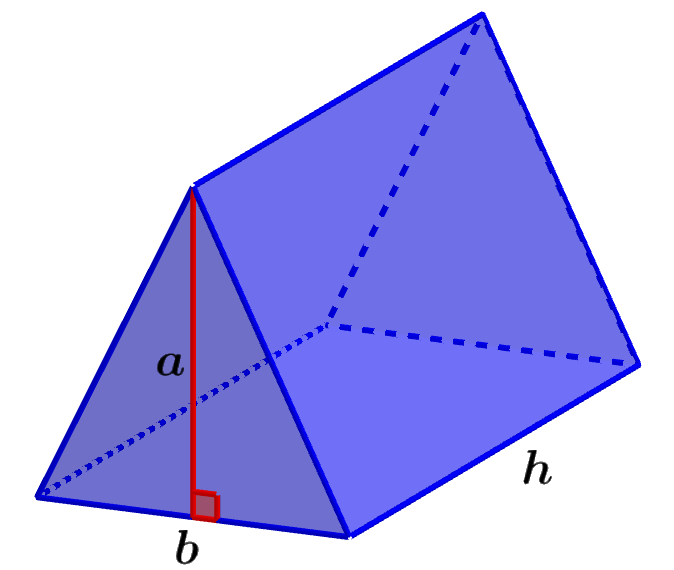
El área de la base del prisma dependerá del tipo de prisma que tengamos. Por ejemplo, en un prisma triangular, podemos calcular el área de su base al multiplicar a un medio de la longitud de la base por la longitud de la altura. Entonces, tenemos la siguiente fórmula:
| $latex V=\frac{1}{2}b\times a\times h$ |
en donde,
- b es la base del triángulo
- a es la altura del triángulo
- h es la altura del prisma
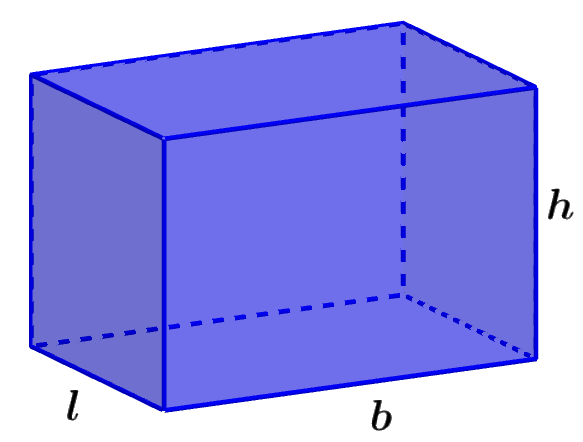
En el caso de un prisma rectangular, podemos calcular el área de su base al multiplicar la longitud del ancho y la longitud de la base. Entonces, tenemos lo siguiente:
| $latex V=l\times b \times h$ |
en donde,
- l es la longitud del ancho del prisma
- b es la longitud de la base del prisma
- h es la longitud de la altura del prisma
Podemos usar estas ideas para calcular el volumen de cualquier prisma.
Área superficial y volumen de prismas – Ejercicios resueltos
En los siguientes ejercicios, tenemos que encontrar el área superficial y el volumen de varios prismas. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es el área superficial de un prisma triangular que tiene una altura de 10 cm y su base triangular tiene lados de longitud 13 cm, 10 cm, 13 cm y una altura de 12 cm?
Solución
Tenemos la siguiente información:
- Altura prisma, $latex h=10$
- Lado 1, $latex b_{1}=13$
- Lado 2, $latex b_{2}=10$
- Lado 3, $latex b_{3}=13$
- Altura triángulo, $latex a=12$
Con esto, podemos encontrar el área de ambas bases triangulares y el área de las tres caras rectangulares laterales. Entonces, tenemos:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$$A_{s}=(12)(10)+(13)(10)+(10)(10)+(13)(10)$$
$latex A_{s}=120+130+100+130$
$latex A_{s}=480$
El área superficial es igual a 480 cm².
EJERCICIO 2
Encuentra el volumen de un prisma que tiene una altura de 8 mm y su base triangular tiene una altura de 6 mm y una base de 7 mm.
Solución
Tenemos lo siguiente:
- Altura de prisma, $latex h=8$
- Altura de triángulo, $latex a=6$
- Base de triángulo, $latex b=7$
Para encontrar el volumen, tenemos que multiplicar el área de la base por la altura del prisma. Entonces, tenemos:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(7)(6)(8)$
$latex V=168$
El volumen es 168 mm³.
EJERCICIO 3
¿Cuál es el área superficial de un prisma rectangular que tiene una base de 7 cm, un ancho de 6 cm y una altura de 8 cm?
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=7$
- Ancho, $latex l=6$
- Altura, $latex h=8$
Tenemos que encontrar las áreas de las seis caras rectangulares, considerando que las caras paralelas tienen la misma área. Entonces, tenemos:
$latex A_{s}=2(bl+lh+hb)$
$latex A_{s}=2((7)(6)+(6)(8)+(8)(7))$
$latex A_{s}=2(42+48+56)$
$latex A_{s}=2(146)$
$latex A_{s}=292$
El área superficial es igual a 292 cm².
EJERCICIO 4
¿Cuál es el volumen de un prisma rectangular que tiene una base de 8 metros, un ancho de 6 metros y una altura de 7 metros.
Solución
Tenemos la siguiente información:
- Base, $latex b=8$
- Ancho, $latex l=6$
- Altura, $latex h=7$
Para encontrar el volumen del prisma rectangular, simplemente tenemos que multiplicar las longitudes de sus tres dimensiones:
$latex V=b \times l \times h$
$latex V=8 \times 6 \times 7$
$latex V=336$
El volumen es igual a 336 m³.
EJERCICIO 5
Determina el área superficial de un prisma triangular que tiene una altura de 5 mm, una base equilátera con lados de 6 mm y una altura de 5.2 mm.
Solución
Tenemos las siguientes longitudes:
- Altura prisma, $latex h=5$
- Lado, $latex b=6$
- Altura triángulo, $latex a=5.2$
Dado que las bases del prisma son triángulos equiláteros, sus lados tienen la misma longitud. Entonces, calculamos su área superficial de la siguiente manera:
$latex A_{s}=ab+bh+bh+bh$
$latex A_{s}=ab+3bh$
$latex A_{s}=(5.2)(6)+3(6)(5)$
$latex A_{s}=31.2+90$
$latex A_{s}=121.2$
El área superficial es igual a 121.2 mm².
EJERCICIO 6
Encuentra el volumen de un prisma que tiene una altura de 8 cm y su base triangular tiene una altura de 6 cm y una base de 7 cm.
Solución
Tenemos las siguientes longitudes:
- Altura de prisma, $latex h=8$
- Altura de triángulo, $latex a=6$
- Base de triángulo, $latex b=7$
Encontramos el volumen del prisma al multiplicar al área de la base triangular por la altura del prisma:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(7)(6)(8)$
$latex V=168$
El volumen es igual a 168 cm³.
EJERCICIO 7
¿Cuál es la longitud de la altura de un prisma rectangular con un área superficial de 148 mm² si es que su base mide 6 mm y su ancho mide 4 mm?
Solución
Tenemos la siguiente información:
- Base, $latex b=6$
- Ancho, $latex l=4$
- Área superficial, $latex A=148$
En este caso, tenemos el área superficial del prisma rectangular y tenemos que encontrar la longitud de la altura. Entonces, usamos la fórmula del área superficial y resolvemos para h:
$latex A_{s}=2(bl+lh+hb)$
$latex 148=2((6)(4)+(4)h+(6)(h))$
$latex 148=2(24+10h)$
$latex 74=24+10h)$
$latex 10h=74-24$
$latex 10h=50$
$latex h=5$
La longitud de la altura es 5 mm.
EJERCICIO 8
¿Cuál es la longitud de la altura de un prisma rectangular que tiene una base de 5 metros, un ancho de 3 metros y un volumen de 90 m³?
Solución
Tenemos lo siguiente:
- Base, $latex b=5$
- Ancho, $latex l=3$
- Volumen, $latex V=90$
En este caso, vamos a usar la fórmula del volumen y resolver para h:
$latex V=b \times l \times h$
$latex 90=5 \times 3 \times h$
$latex 90=15h$
$latex h=6$
La longitud de la altura es 6 m.
EJERCICIO 9
Encuentra el área superficial de un prisma hexagonal que tiene una altura de 5 cm y una base hexagonal con lados de longitud 3 cm.
Solución
Tenemos la siguiente información:
- Lados hexágono, $latex a=3$
- Altura prisma, $latex h=5$
Un prisma hexagonal tiene dos bases hexagonales y seis caras laterales rectangulares. El área de las seis caras rectangulares es igual a 6ah y el Área de las caras hexagonales es igual a $latex 3\sqrt{3}{{a}^2}$. Entonces, tenemos:
$latex A_{s}=3\sqrt{3}{{a}^2}+6ah$
$latex A_{s}=3\sqrt{3}{{(3)}^2}+6(3)(5)$
$latex A_{s}=3\sqrt{3}(9)+90$
$latex A_{s}=46.77+90$
$latex A_{s}=136.77$
El área superficial es igual a 136.77 cm².
EJERCICIO 10
Calcula el volumen de un prisma hexagonal que tiene lados de longitud 4 cm y una altura de 6 cm.
Solución
Tenemos las siguientes longitudes.
- Lados del hexágono, $latex a=4$
- Altura, $latex h=6$
El volumen del prisma hexagonal es igual al área de la base hexagonal multiplicada por la altura del prisma:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(4)}^2}(6)$
$latex V=\frac{3\sqrt{3}}{2}(16)(6)$
$latex V=249.4$
El volumen es igual a 249.4 cm³.
Área superficial y volumen de prismas – Ejercicios para resolver
Usa todo lo aprendido sobre el área superficial y el volumen de un prisma para resolver los siguientes ejercicios.
Véase también
¿Interesado en aprender más sobre prismas rectangulares? Mira estas páginas: