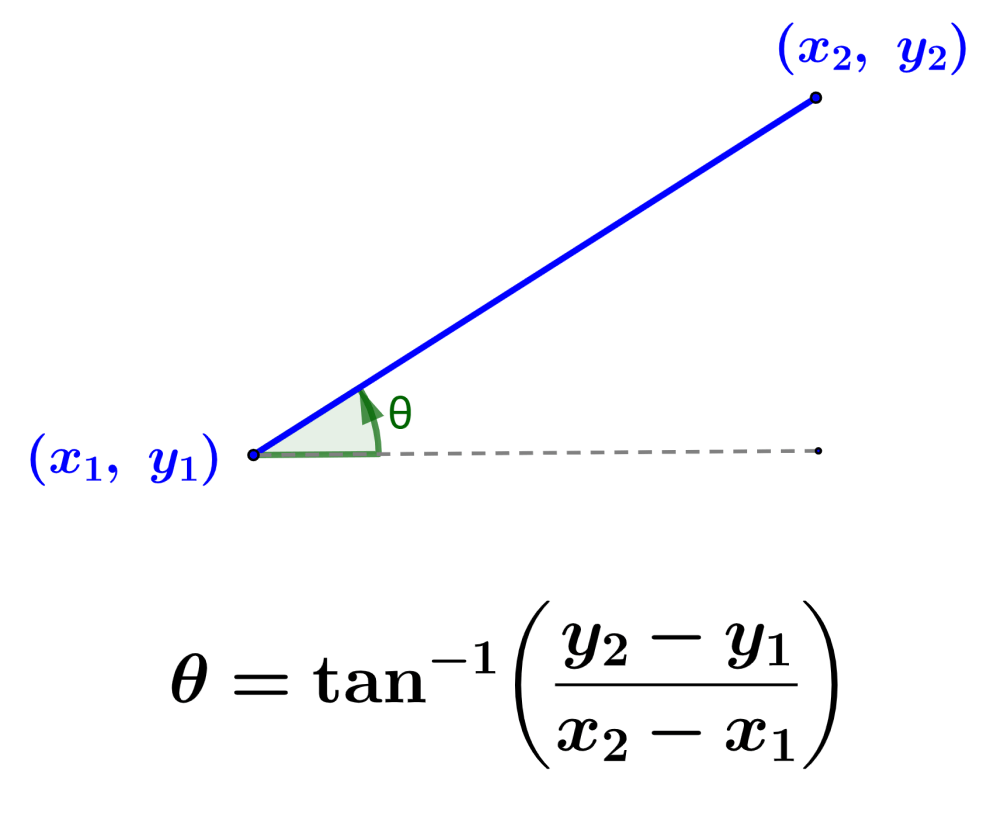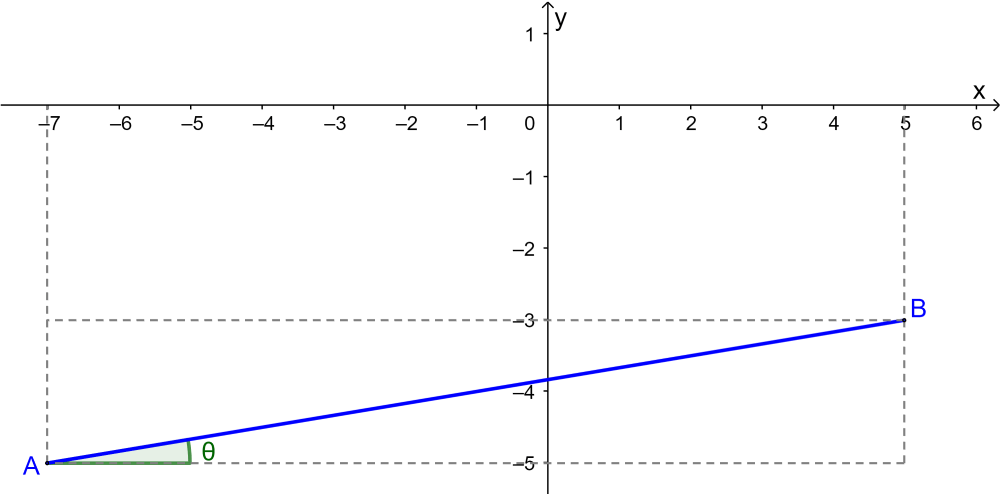El ángulo de inclinación de una recta o el ángulo de la pendiente de la recta es el ángulo formado por la recta y su componente horizontal. Para obtener el valor de este ángulo, tenemos que usar trigonometría, específicamente la función tangente. El ángulo puede ser positivo o negativo dependiendo en la dirección en la que sea medido.
A continuación, conoceremos cómo calcular el ángulo de inclinación de una recta. Veremos su fórmula, algunas consideraciones importantes y varios ejercicios resueltos.
Fórmula del ángulo de la inclinación de una recta o de su pendiente
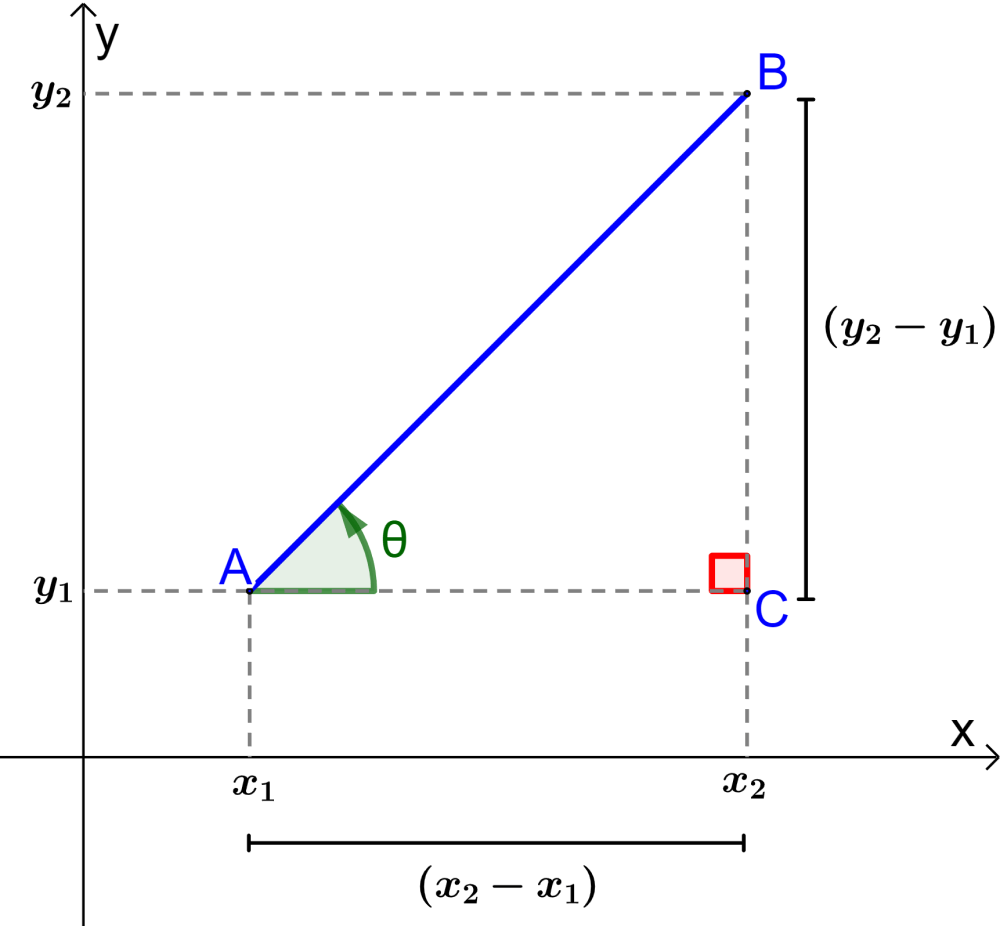
Para encontrar la fórmula del ángulo de la inclinación de una recta, vamos a usar el siguiente diagrama:
Podemos ver que el diagrama tiene un triángulo rectángulo ABC formado por los componentes horizontal y vertical de la recta. En el diagrama, θ es el ángulo formado por la recta AB y su componente horizontal.
Usando trigonometría y recordando que la tangente de un ángulo es igual al lado opuesto sobre el lado adyacente, tenemos $latex \tan(\theta)=\frac{BC}{AC}$.
Ahora, usando el diagrama, podemos observar que $latex \frac{BC}{AC}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$, lo cual es igual a la pendiente de la recta AB.
Entonces, tenemos lo siguiente:
$$\tan(\theta)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
Observaciones importantes:
- Si es que $latex m$ es la pendiente de la recta AB, entonces, el ángulo de inclinación de la recta es igual a $latex \tan^{-1}(m)$.
- Cuando el resultado de $latex \tan^{-1}(m)$ es negativo, el ángulo θ es medido desde la línea horizontal hasta la recta en dirección de las manecillas del reloj.
Ángulo de inclinación de una recta – Ejercicios resueltos
La fórmula del ángulo de inclinación de una recta es usada para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra el ángulo formado por la recta que tiene los puntos A=(-7, -5) y B=(5, -3) con respecto a la horizontal.
Solución
Obteniendo una gráfica simple, tenemos:
Para encontrar el ángulo θ, vamos a usar la fórmula del ángulo de inclinación de una recta:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{-3-(-5)}{5-(-7)}\right)$$
$$=\tan^{-1}\left(\frac{-3+5}{5+7}\right)$$
$$=\tan^{-1}\left(\frac{2}{12}\right)$$
$$=\tan^{-1}\left(\frac{1}{6}\right)$$
$$\theta=9.46^{\circ}$$
EJERCICIO 2
Encuentra el ángulo de inclinación de la recta que tiene los puntos A=(5, -4) y B=(-6, 7).
Solución
Podemos encontrar el ángulo θ, al usar la fórmula del ángulo de inclinación de una recta con las coordenadas de los dos puntos dados:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{7-(-4)}{-6-5}\right)$$
$$=\tan^{-1}\left(\frac{7+4}{-6-5}\right)$$
$$=\tan^{-1}\left(\frac{11}{-11}\right)$$
$$=\tan^{-1}\left(-1\right)$$
$$\theta=-45^{\circ}$$
EJERCICIO 3
Una recta pasa por los puntos A=(7, -2) y B=(3, -5). Encuentra el ángulo de la pendiente de AB.
Solución
Vamos a encontrar el ángulo θ usando la fórmula del ángulo de inclinación de una recta con las coordenadas de los puntos dados:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{-5-(-2)}{3-7}\right)$$
$$=\tan^{-1}\left(\frac{-5+2}{3-7}\right)$$
$$=\tan^{-1}\left(\frac{-3}{-4}\right)$$
$$=\tan^{-1}\left(\frac{3}{4}\right)$$
$$\theta=36.9^{\circ}$$
EJERCICIO 4
Determina el ángulo de la pendiente de la recta que pasa por los puntos A=(6, 7) y B=(12, 7).
Solución
Usando las coordenadas de los puntos en la fórmula del ángulo de la pendiente, tenemos:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{7-7}{12-6}\right)$$
$$=\tan^{-1}\left(\frac{0}{6}\right)$$
$$\theta=0^{\circ}$$
Obtuvimos un ángulo igual a 0°. Esto significa que la recta es horizontal.
Mirando las coordenadas en y de ambos puntos, vemos que son iguales. Esto solo sucede cuando una recta es horizontal.
EJERCICIO 5
Encuentra el ángulo de la pendiente de la recta que pasa por los puntos A=(3, 7) y B=(-6, 11).
Solución
Podemos encontrar el ángulo de la pendiente al usar la fórmula con las coordenadas de los puntos dados:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{11-7}{-6-3}\right)$$
$$=\tan^{-1}\left(-\frac{4}{9}\right)$$
$$\theta=-24^{\circ}$$
EJERCICIO 6
Encuentra el ángulo formado por la recta que pasa por los puntos A=(5, -3) y B=(5, 2).
Solución
Para encontrar el ángulo θ, usamos las coordenadas de los puntos dados en la fórmula del ángulo de inclinación:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{2-(-3)}{5-5}\right)$$
$$=\tan^{-1}\left(\frac{-2-3}{5-5}\right)$$
$$=\tan^{-1}\left(\frac{-5}{0}\right)$$
$$=\tan^{-1}\left(\text{infinito}\right)$$
$$\theta=90^{\circ}$$
En este caso, obtuvimos -5/0, lo cual es igual a infinito. Mirando a las coordenadas de x de ambos puntos, vemos que ambas son igual a 5. Esto solo sucede cuando tenemos una recta vertical.
Una recta vertical es perpendicular con la horizontal, por lo que el ángulo es igual a 90°.
Ángulo de inclinación de una recta – Ejercicios para resolver
Usa la fórmula del ángulo de inclinación de la pendiente de una recta para resolver los siguientes ejercicios.
Véase también
¿Interesado en aprender más sobre rectas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
