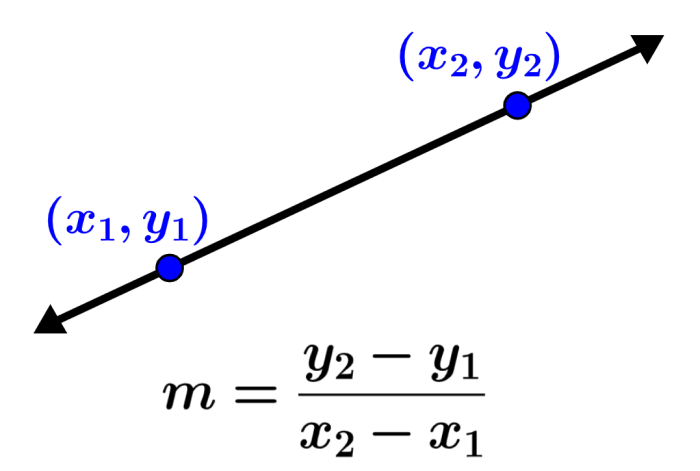
Podemos calcular la pendiente de una línea usando dos puntos que son parte de la línea. Entonces, formamos una fracción, en donde el numerador corresponde al cambio en las coordenadas y de los puntos y el denominador corresponde al cambio en las coordenadas x.
A continuación, conoceremos la fórmula que podemos aplicar para calcular la pendiente usando dos puntos. Luego, aplicaremos esta fórmula para resolver algunos ejercicios.
Fórmula para la pendiente usando dos puntos
Podemos encontrar la fórmula de la pendiente al usar las coordenadas de dos puntos que son parte de la recta. La pendiente es igual al cambio en y dividido por el cambio en x. Entonces, si es que tenemos los puntos $latex A=(x_{1}, y_{1})$ y $latex B=(x_{2}, y_{2})$, la fórmula de la pendiente es:
| Fórmula de la pendiente $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ |
Pendiente de rectas comunes
Usando la fórmula de la pendiente, podemos determinar la pendiente de algunas rectas comunes para que nos sirvan de referencia.
Pendiente de una recta horizontal
Una recta horizontal no tiene inclinación con respecto al eje x, por lo que su pendiente es igual a 0. Las coordenadas en y de todos los puntos en una recta horizontal son las mismas, por lo que al usar la fórmula de la pendiente, tenemos:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{0}{x_{2}-x_{1}}$
$latex m=0$
Pendiente de una recta vertical
Una recta vertical tiene una pendiente indefinida. Todos los puntos en una recta vertical tienen coordenadas en x que son las mismas, por lo que al aplicar la fórmula de la pendiente, tenemos:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{y_{2}-y_{1}}{0}$
Sabemos que la división por 0 es indefinida.
Pendiente de líneas paralelas
Para que dos o más líneas sean paralelas, sus pendientes deben ser iguales. Por ejemplo, supongamos que tenemos las líneas $latex l_{1}$ y $latex l_{2}$ con pendientes $latex m_{1}$ y $latex m_{2}$ respectivamente. Si es que estas líneas son paralelas, debemos tener:
$latex m_{1}=m_{2}$
Pendiente de líneas perpendiculares
Las pendientes de dos líneas paralelas son iguales al recíproco negativo la una de la otra. Por ejemplo, supongamos que tenemos las líneas $latex l_{1}$ y $latex l_{2}$ con pendientes $latex m_{1}$ y $latex m_{2}$ respectivamente. Si es que estas líneas son perpendiculares, debemos tener:
$latex m_{1}=-\frac{1}{m_{2}}$
Pendiente de una recta con dos puntos ejercicios resueltos
La fórmula de la pendiente de una recta es aplicada usando los dos puntos dados para obtener la respuesta. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Tenemos una recta que contienen a los puntos (1, 3) y (3, 7). ¿Cuál es su pendiente?
Solución
Tenemos los dos puntos:
- $latex (x_{1}, y_{1})=(1, 3)$
- $latex (x_{2}, y_{2})=(3, 7)$
Aplicamos la fórmula de la pendiente con los dos puntos dados:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{7-3}{3-1}$
$latex m=\frac{4}{2}$
$latex m=2$
La pendiente de la recta es 2.
EJERCICIO 2
¿Cuál es la pendiente de una recta que tiene los puntos (3, 2) y (8, 3)?
Solución
Tenemos las siguientes coordenadas de los puntos:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(8, 3)$
Usamos estas coordenadas en la fórmula de la pendiente y tenemos:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{3-2}{8-3}$
$latex m=\frac{1}{5}$
La pendiente de la recta es $latex \frac{1}{5}$.
EJERCICIO 3
Los puntos (-1, 3) y (6, -4) son parte de una recta. ¿Cuál es su pendiente?
Solución
Tenemos los siguientes puntos:
- $latex (x_{1}, y_{1})=(-1, 3)$
- $latex (x_{2}, y_{2})=(6, -4)$
Cuando aplicamos la fórmula de la pendiente con estas coordenadas, tenemos:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-4-3}{6-(-1)}$
$latex m=\frac{-7}{7}$
$latex m=-1$
La pendiente de la recta es $latex -1$.
EJERCICIO 4
¿Cuál es la pendiente de una recta que contiene a los puntos (-3, -2) y (3, -5)?
Solución
Podemos escribir de la siguiente manera:
- $latex (x_{1}, y_{1})=(-3, -2)$
- $latex (x_{2}, y_{2})=(3, -5)$
Usamos la fórmula de la pendiente con las coordenadas dadas:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-5-(-2)}{3-(-3)}$
$latex m=\frac{-3}{6}$
$latex m=-\frac{1}{2}$
La pendiente de la recta es $latex -\frac{1}{2}$.
Pendiente de una recta con dos puntos ejercicios para resolver
Resuelve los siguientes ejercicios de práctica usando la fórmula de la pendiente con los puntos dados. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre punto medio, distancia y pendiente en el plano? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
