La distancia entre dos puntos puede ser calculada usando la fórmula de la distancia. Por su parte, la fórmula de la distancia es derivada usando el teorema de Pitágoras en el plano cartesiano, en donde la distancia representa a la hipotenusa de un triángulo rectángulo y las distancias en x y y representan a los catetos del triángulo.
A continuación, aprenderemos a derivar la fórmula de la distancia entre dos puntos. Además, usaremos esta fórmula para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a determinar la distancia entre dos puntos con ejemplos.
GEOMETRÍA
Relevante para…
Aprender a determinar la distancia entre dos puntos con ejemplos.
Fórmula de la distancia entre dos puntos
La distancia entre dos puntos con coordenadas $latex (x_{1},~y_{1})$ y $latex (x_{2},~y_{2})$ puede ser calculada usando la fórmula de la distancia.
| Fórmula de la distancia $latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$ |
Esta es la fórmula que puede ser aplicada en el plano cartesiano, es decir, en el espacio bidimensional. Adicionalmente, si es que queremos calcular la distancia entre dos puntos ubicados en el plano tridimensional, tenemos que usar la fórmula de la distancia en 3D:
| Fórmula de la distancia en 3D $$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(z_{2}-z_{1})}^2}}$$ |
¿Cómo derivar la fórmula para la distancia entre dos puntos?
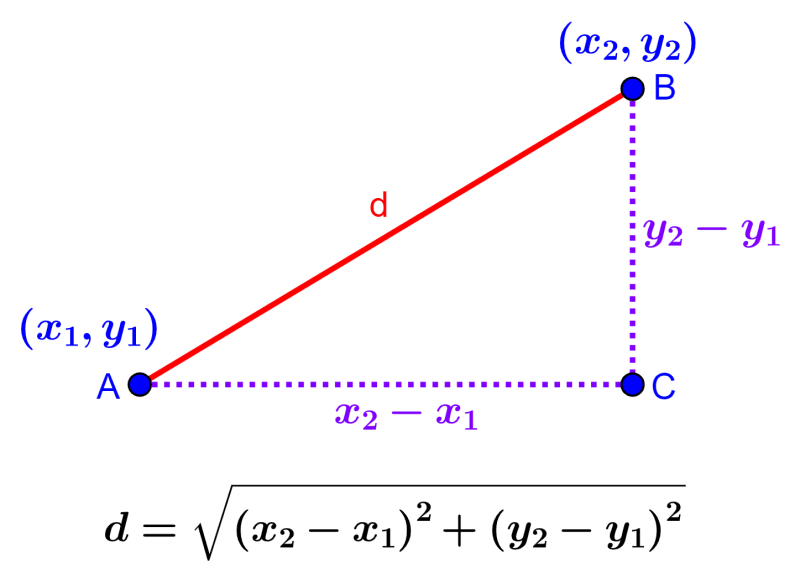
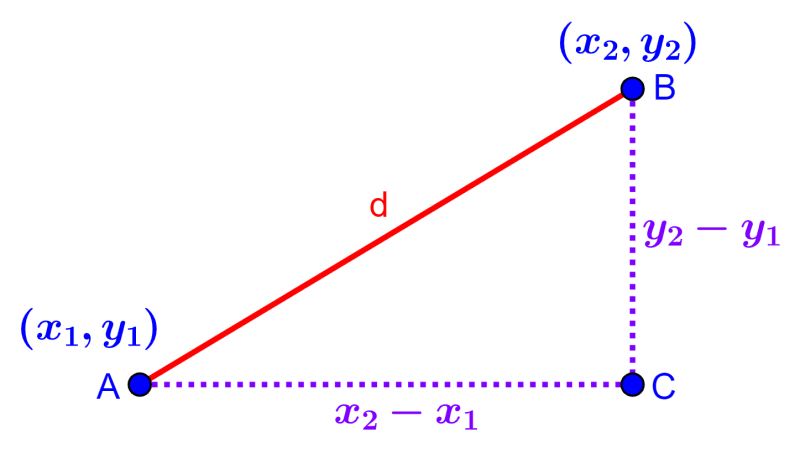
Para derivar la fórmula de la distancia entre dos puntos, tenemos que usar al teorema de Pitágoras en el plano cartesiano. Entonces, vamos a usar el siguiente diagrama:
En el diagrama, tenemos los puntos $latex A=(x_{1},y_{1})$ y $latex B=(x_{2},y_{2})$. Unimos a estos puntos con el segmento AB, al cual podemos denotar con d. Luego, construimos un triángulo rectángulo en donde el segmento AB es la hipotenusa y los segmentos AC y BC son los catetos del triángulo.
Cuando aplicamos el teorema de Pitágoras al triángulo ABC, tenemos:
$latex {{AB}^2}={{AC}^2}+{{BC}^2}$
Podemos observar que, la distancia vertical entre los puntos es igual a $latex |y_{2}-y_{1}|$ y la distancia horizontal entre los puntos es igual a $latex |x_{2}-x_{1}|$. Además, si es que sustituimos AB con d, tenemos:
$latex {{d}^2}={{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}$
Ahora, sacamos la raíz cuadrada de ambos lados para obtener la fórmula de la distancia:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
Distancia entre dos puntos ejemplos resueltos
La fórmula de la distancia es usada en los siguientes ejemplos para obtener la distancia entre dos puntos. Cada ejemplo tiene su respectiva solución, pero es recomendable que intentes resolver los ejemplos tú mismo para practicar.
EJEMPLO 1
Determina la distancia entre los puntos (1, 3) y (5, 6).
Solución
Escribimos las coordenadas de los puntos de la siguiente forma:
- $latex (x_{1}, y_{1})=(1, 3)$
- $latex (x_{2}, y_{2})=(5, 6)$
Usando la fórmula de la distancia con estos valores, tenemos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(5-1)}^2}+{{(6-3)}^2}}$
$latex =\sqrt{{{(4)}^2}+{{(3)}^2}}$
$latex =\sqrt{16+9}$
$latex =\sqrt{25}$
$latex =5$
La distancia entre los puntos es igual a 5.
EJEMPLO 2
¿Cuál es la distancia entre los puntos (2, 6) y (7, 10)?
Solución
Podemos escribir a las coordenadas de los puntos de la siguiente forma:
- $latex (x_{1}, y_{1})=(2, 6)$
- $latex (x_{2}, y_{2})=(7, 10)$
Aplicamos la fórmula de la distancia con las coordenadas dadas:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(7-2)}^2}+{{(10-6)}^2}}$
$latex =\sqrt{{{(5)}^2}+{{(4)}^2}}$
$latex =\sqrt{25+16}$
$latex =\sqrt{51}$
$latex =7.14$
La distancia es igual a 7.14.
EJEMPLO 3
Si es que tenemos los puntos (12, 2) y (5, 5), ¿cuál es su distancia?
Solución
Podemos observar las siguientes coordenadas
- $latex (x_{1}, y_{1})=(12, 2)$
- $latex (x_{2}, y_{2})=(5, 5)$
Cuando sustituimos a estos valores en la fórmula de la distancia, tenemos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(5-12)}^2}+{{(5-2)}^2}}$
$latex =\sqrt{{{(-7)}^2}+{{(3)}^2}}$
$latex =\sqrt{49+9}$
$latex =\sqrt{68}$
$latex =7.62$
La distancia entre los puntos es igual a 7.62.
EJEMPLO 4
Encuentra la distancia entre los puntos (-4, 5) y (4, 9).
Solución
Tenemos las siguientes coordenadas:
- $latex (x_{1}, y_{1})=(-4, 5)$
- $latex (x_{2}, y_{2})=(4, 9)$
Aquí, tenemos un punto con coordenadas negativas. Sin embargo, la fórmula de la distancia puede ser usada sin importar los signos de las coordenadas.
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(4-(-4))}^2}+{{(9-5)}^2}}$
$latex =\sqrt{{{(8)}^2}+{{(4)}^2}}$
$latex =\sqrt{64+16}$
$latex =\sqrt{80}$
$latex =8.94$
La distancia es igual a 8.94.
EJERCICIO 5
Determina la distancia entre los puntos (-6, -7) y (-2, -1).
Solución
Tenemos las siguientes coordenadas:
- $latex (x_{1}, y_{1})=(-6, -7)$
- $latex (x_{2}, y_{2})=(-2, -1)$
Similar al ejercicio anterior, sólo tenemos que usar la fórmula de la distancia con las coordenadas dadas.
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(-2-(-6))}^2}+{{(-1-(-7))}^2}}$
$latex =\sqrt{{{(4)}^2}+{{(6)}^2}}$
$latex =\sqrt{16+36}$
$latex =\sqrt{52}$
$latex =7.21$
La distancia es igual a 7.21.
Distancia entre dos puntos ejemplos para resolver
Los siguientes ejercicios pueden ser resueltos usando lo aprendido sobre la distancia entre dos puntos. Puedes mirar la fórmula de la distancia escrita arriba o los ejemplos resolvidos en caso de necesitar ayuda.
Véase también
¿Interesado en aprender más sobre punto medio, distancia y pendiente en el plano? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
