La forma pendiente intercepto de una recta es una de las más comúnmente usadas para encontrar la ecuación de una recta. Cuando conocemos el intercepto en y (b) y la pendiente de la recta (m), podemos usar la forma y=mx+b. La ecuación de la recta satisface a cualquier punto que se ubica en la recta.
A continuación, aprenderemos todo lo relacionado a la forma pendiente intercepto de una recta. Aprenderemos a derivar su fórmula y la aplicaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender encontrar la ecuación de una recta usando la forma pendiente intercepto.
GEOMETRÍA
Relevante para…
Aprender encontrar la ecuación de una recta usando la forma pendiente intercepto.
Fórmula de la forma pendiente intercepto de una recta
Existen diferentes métodos que podemos usar para determinar la ecuación de una recta en el plano cartesiano. Todo dependerá de la información que tengamos disponible.
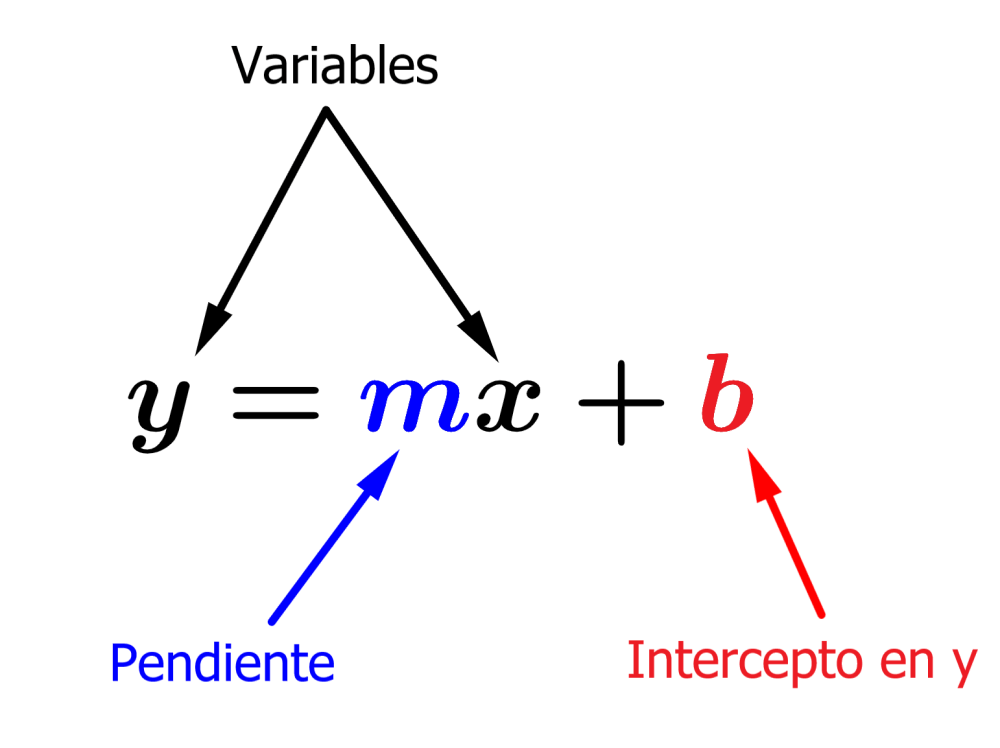
Si es que conocemos el intercepto en y y la pendiente de la recta, podemos usar la forma pendiente intercepto: y=mx+b.
El intercepto en y es la coordenada en y en donde la recta interseca al eje y. El intercepto en y es representado por la letra b y comúnmente dado en la forma (0, b).
La pendiente de una recta representa el cambio en las coordenadas en y con respecto a las coordenadas en x. Una pendiente positiva indica que la recta crece de izquierda a derecha y una pendiente negativa indica que la recta decrece de izquierda a derecha.
Las variables x y y se mantienen de la misma forma cuando usamos la fórmula de la forma pendiente intercepto ya que (x, y) representa a todos los puntos que se ubican en la recta.
Derivación de la fórmula de la forma punto pendiente de una recta
Para derivar la fórmula de la forma punto pendiente de una recta, vamos a usar la siguiente gráfica:
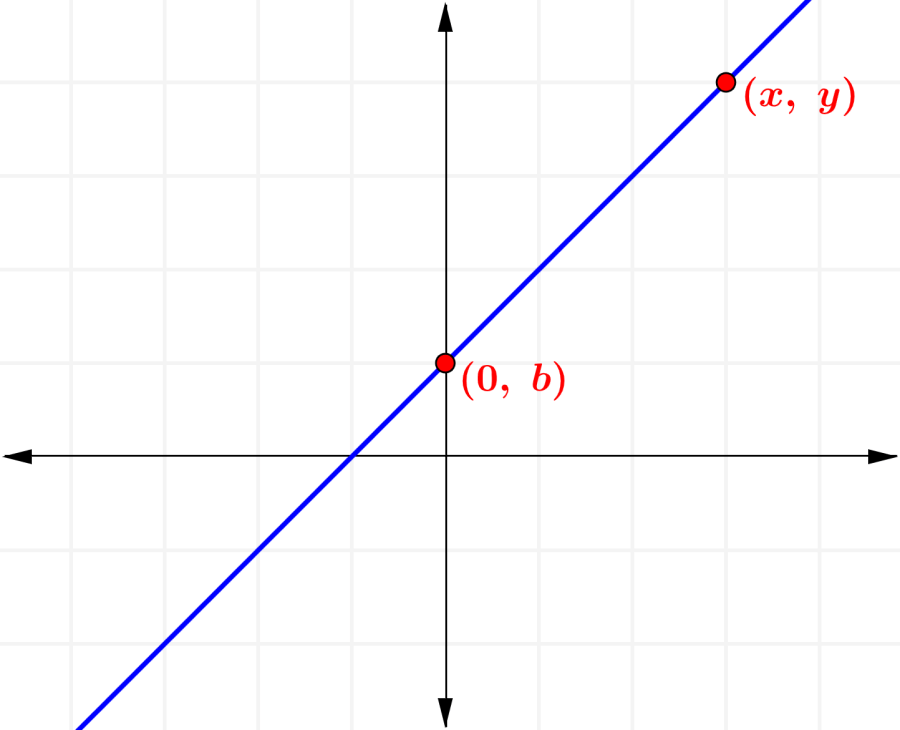
Aquí, tenemos una recta que tiene una pendiente igual a m y que interseca al eje y en el punto (0, b). Además, consideramos al punto (x, y), el cual es un punto arbitrario que se ubica en la recta.
Ahora, dado que los puntos (0, b) y (x, y) son simplemente dos puntos en la recta, podemos escribir de la siguiente manera:
$latex (x_{1},~y_{1})=(0,~b)$
$latex (x_{2},~y_{2})=(x,~y)$
Recordemos que la Fórmula de la Pendiente de una Recta usando dos puntos es la siguiente:
$$m=\frac{(y_{2}-y_{1}}{x_{2}-x_{1}}$$
Entonces, si es que usamos esta fórmula para encontrar la pendiente de la recta de arriba, tenemos:
$$m=\frac{(y-b)}{(x-0)}$$
$$m=\frac{(y-b}{x}$$
Podemos resolver esta ecuación para y:
$$m=\frac{(y-b}{x}$$
$latex mx=y-b$
$latex y=mx+b$
Entonces, hemos derivado la fórmula de la forma pendiente intercepto de una recta.
Forma pendiente intercepto de una recta – Ejercicios resueltos
Los siguientes ejercicios son resueltos aplicando la forma pendiente intercepto de una recta. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es la ecuación de una recta que tiene una pendiente de 1/2 y su intercepto en y es (0, -2).
Solución
Para encontrar la ecuación de la recta, usamos la forma pendiente intercepto con la siguiente información:
- m = 1/2
- b = -2
$latex y=mx+b$
$latex y=\frac{1}{2}x-2$
La ecuación de la recta dada es $latex y=\frac{1}{2}x-2$.
EJERCICIO 2
¿Cuál es la ecuación de una línea que tiene una pendiente de -2 y un intercepto en y de (0, 3)?
Solución
Aplicamos la fórmula de la forma pendiente intercepto con la siguiente información:
- m = -2
- b = 3
$latex y=mx+b$
$latex y=-2x+3$
La ecuación de la recta dada es $latex y=-2x+3$.
EJERCICIO 3
¿Cuál es la ecuación de una recta horizontal que tiene interseca con el eje y en (0, -5)?
Solución
En este caso, no tenemos la pendiente dada explícitamente. Sin embargo, se indica que la línea es horizontal y sabemos que una línea horizontal no tiene cambios en el eje y, por lo que su pendiente es igual a 0.
Entonces, tenemos la siguiente información:
- m = 0
- b = -5
Usando la forma pendiente intercepto, tenemos:
$latex y=mx+b$
$latex y=0x-5$
$latex y=-5$
La ecuación de la recta horizontal es $latex y=-5$. En una recta horizontal, los valores de y se mantienen constantes.
EJERCICIO 4
Determina la ecuación de una recta que es paralela a la recta y=5x+2 y que tiene un intercepto en y en (0, -3).
Solución
En este ejercicio, tampoco tenemos la pendiente de la recta dada explícitamente. Sin embargo, tenemos que la recta es paralela a y=5x+2 y sabemos que líneas paralelas tienen la misma pendiente.
Entonces, tenemos la siguiente información:
- m = 5
- b = -3
$latex y=mx+b$
$latex y=5x-3$
La ecuación de la recta dada es $latex y=5x-3$.
EJERCICIO 5
Si es que una recta es paralela a la recta y=-x+10 e interseca al eje y en (0, 3), encuentra su ecuación.
Solución
Similar al ejercicio anterior, sabemos que líneas paralelas tienen la misma pendiente, por lo que tenemos:
- m = -1
- b = 3
$latex y=mx+b$
$latex y=-x+3$
La ecuación de la recta es $latex y=-x+3$.
EJERCICIO 6
Determina la ecuación de una recta que tiene una pendiente de 1/5 y que pasa por el origen.
Solución
En este caso, conocemos la pendiente, pero no tenemos el intercepto en y dado explícitamente. Sin embargo, tenemos que la recta pasa por el origen, es decir, el punto (0, 0), por lo que tenemos lo siguiente:
- m = 1/5
- b = 0
$latex y=mx+b$
$latex y=\frac{1}{5}x+0$
$latex y=\frac{1}{5}x$
La ecuación de la recta es $latex y=\frac{1}{5}x$.
EJERCICIO 7
Si es que una recta tiene una pendiente de 0.25 y un intercepto en y en (0, 0.5), ¿cuál es su ecuación?
Solución
Tenemos que usar la fórmula de la forma pendiente intercepto con los siguientes valores:
- m = 0.25
- b = 0.5
$latex y=mx+b$
$latex y=0.25x+0.5$
La ecuación de la recta dada es $latex y=0.25x+0.5$.
Forma pendiente intercepto de una recta – Ejercicios para resolver
Aplica la fórmula de la forma pendiente intercepto para encontrar las ecuaciones de las rectas en estos ejercicios. Si tienes problema con estos ejercicios, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
