La distancia de un punto a una recta es la distancia más corta que puede unir a una línea recta con el punto. La distancia más corta siempre será un segmento perpendicular a la línea. Podemos derivar una fórmula para la distancia de un punto a una recta usando trigonometría y la ecuación de una recta.
A continuación, conoceremos la fórmula que podemos usar para calcular la distancia de un punto a una recta. Además, usaremos esta fórmula para resolver algunos problemas de práctica.
¿Qué es la distancia de un punto a una recta?
La distancia desde un punto hasta una recta es la distancia más corta que puede unirlos. Es decir, es la menor longitud posible que necesitamos para movernos desde el punto hasta un punto en la recta. Esta distancia siempre será perpendicular a la recta dada.
Por ejemplo, vamos a considerar la siguiente recta L y un punto p que no es parte de la recta:
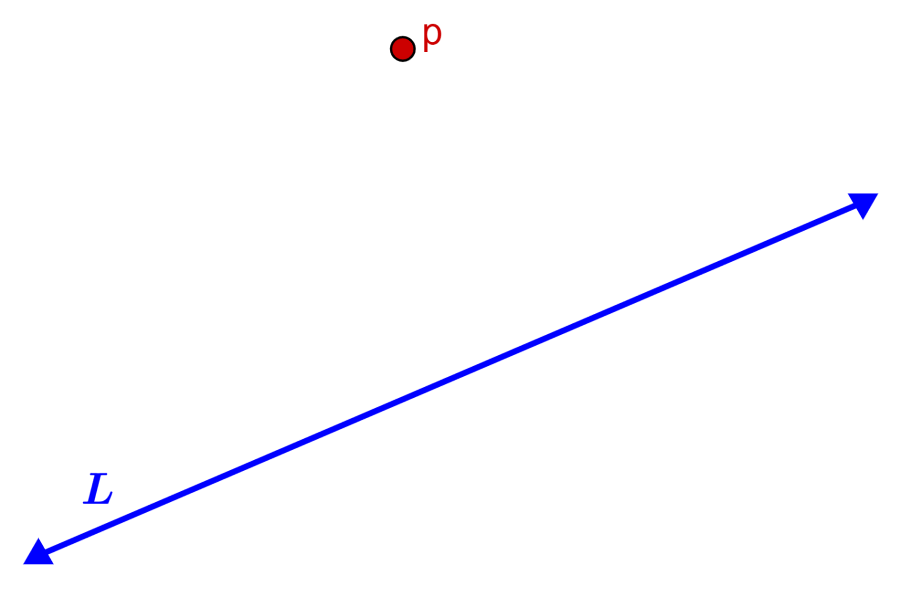
Para medir la distancia desde la recta hasta el punto p, podemos usar la ecuación de una recta y la fórmula de la distancia. Además, también consideramos a un triángulo rectángulo XYZ, el cual tiene un ángulo recto en Y:
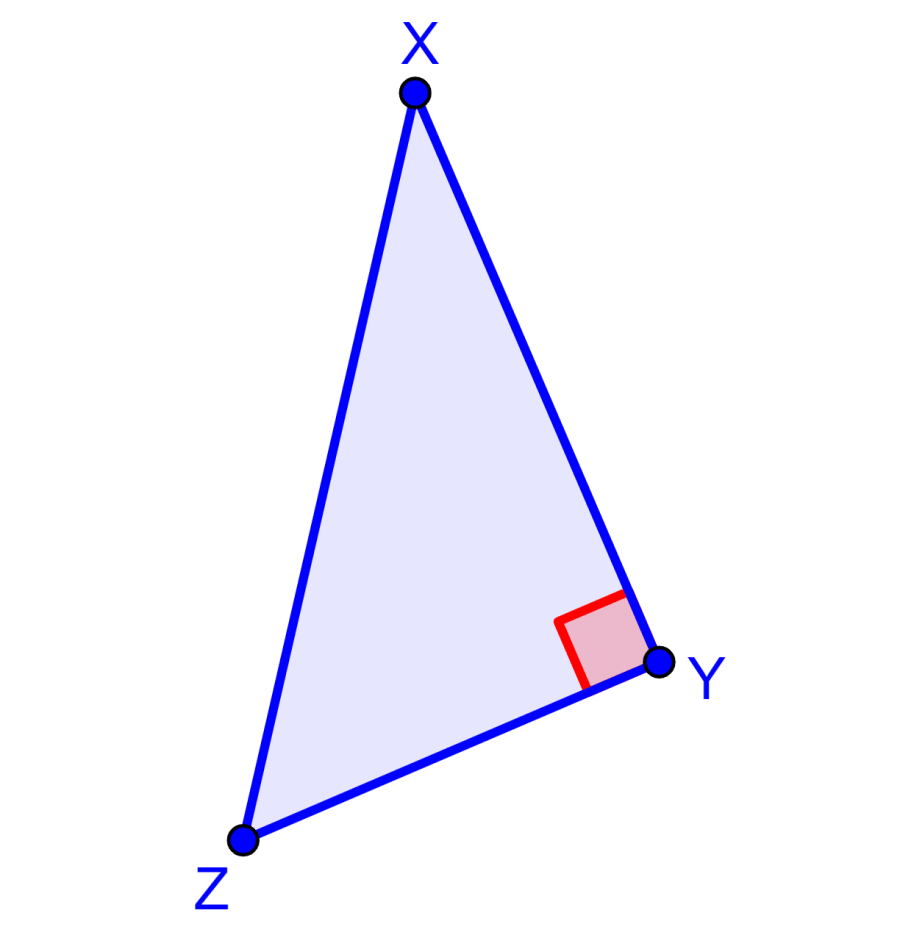
En este triángulo, ángulo Y mide 90° y el segmento XZ es la hipotenusa. La hipotenusa XZ siempre será más larga que el segmento perpendicular que va desde X hasta YZ. Entonces, podemos usar esto en el siguiente diagrama:
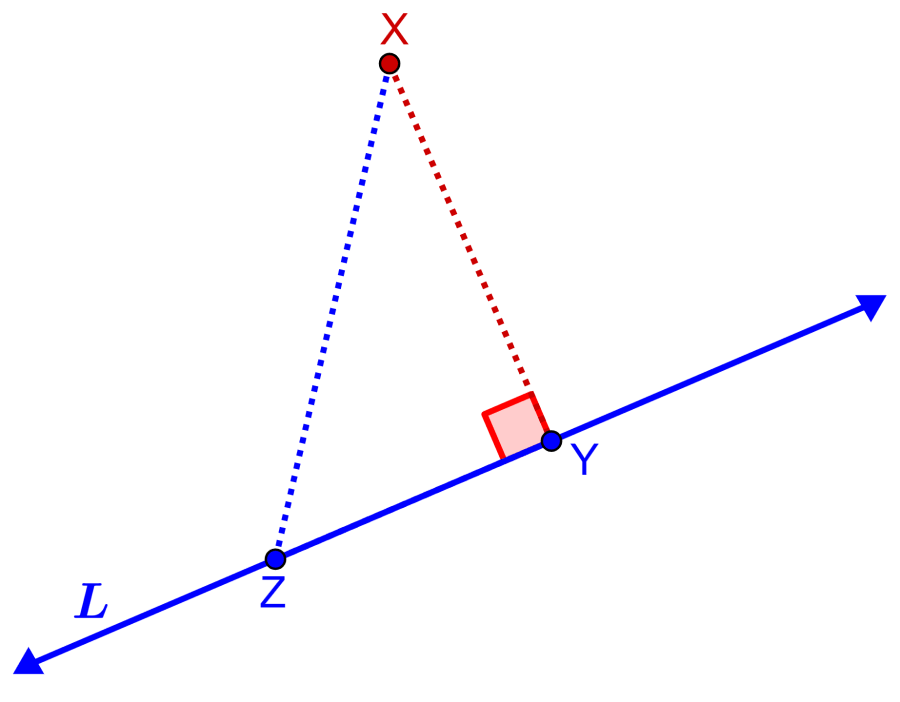
El segmento XY es perpendicular a la recta L. Por otro lado, Z puede ser cualquier punto en la recta R. Podemos observar que XY siempre será corto que XZ sin importar en dónde Z esté ubicado en la recta.
Esto significa que, la distancia más corta desde un punto hasta una recta siempre será un segmento perpendicular desde el punto hasta la recta.
Derivación de la fórmula de la distancia de un punto a una recta
La distancia perpendicular a un punto $latex P(x_{1},~y_{1})$ desde una recta $latex ax+by+c=0$ puede ser encontrada usando la siguiente fórmula:
| $$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$ |
Podemos derivar esta fórmula usando el siguiente diagrama:
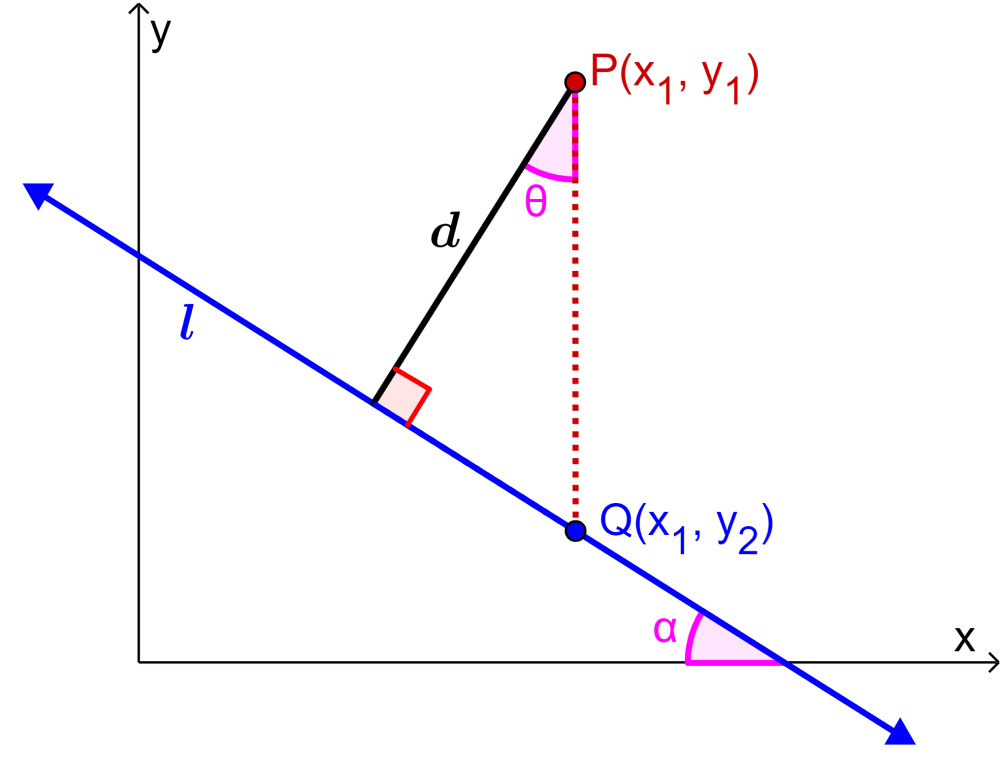
El punto $latex Q(x_{1},~y_{2})$ se ubica en la recta $latex ax+by+c=0$ y está directamente debajo de P.
Usando al punto Q en la ecuación de la recta, tenemos $latex ax_{1}+by_{2}+c=0$. Si es que resolvemos para $latex y_{2}$, tenemos:
$$y_{2}=-\left(\frac{ax_{1}+c}{b}\right)$$
Dado que los puntos P y Q están en la misma coordenada de x, tenemos: $latex PQ=y_{1}-y_{2}$. Usando esto en la ecuación obtenida anteriormente, tenemos:
$$PQ=y_{1}+\frac{ax_{1}+c}{b}$$
$$=\frac{ax_{1}+by_{1}+c}{b}$$
Ahora, mirando el diagrama, podemos deducir que d es igual al coseno de θ multiplicado por PQ: $latex d=PQ\cos(\theta)$. Entonces, tenemos:
$$d=\frac{ax_{1}+by_{1}+c}{b}\cos(\theta)~~[1]$$
Solo nos queda encontrar una expresión para cos(θ) para completar la derivación de la fórmula.
Usando el diagrama nuevamente junto con teoremas de ángulos, podemos deducir que el ángulo θ es igual al ángulo α. Además, dado que podemos escribir a la ecuación de la recta l como $latex y=-\frac{a}{b}x-c$, la pendiente de l es $latex-\frac{a}{b}$.
Esto significa que $latex \tan(\theta)=\tan(\alpha)=\frac{a}{b}$. Recordando que tangente es igual al lado opuesto sobre el lado adyacente, podemos obtener el siguiente diagrama, en donde, usamos el teorema de Pitágoras para obtener la hipotenusa:
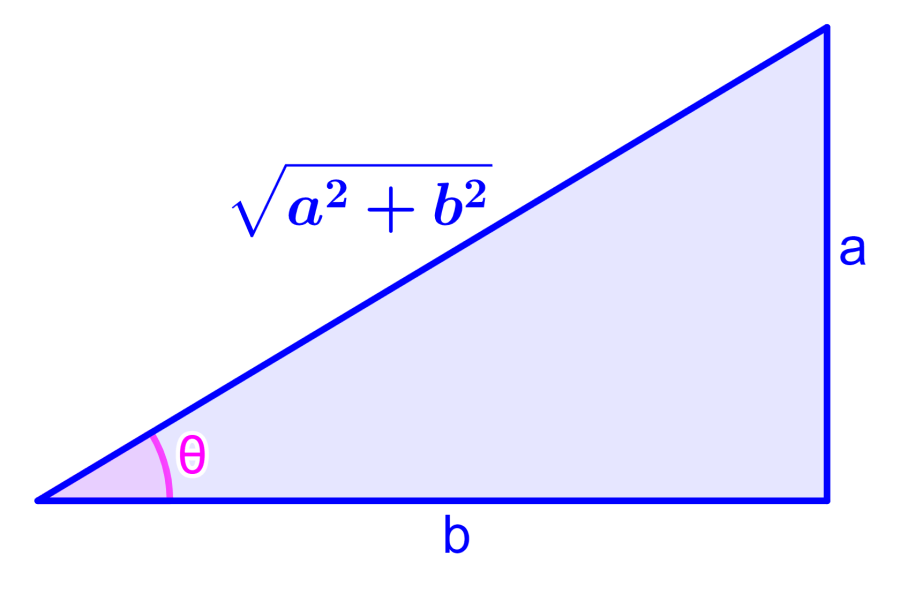
Entonces, tenemos:
$$\cos(\theta)=\frac{b}{\sqrt{a^2+b^2}}~~[2]$$
Sustituyendo la ecuación [2] en la ecuación [1], tenemos:
$$d=\left(\frac{ax_{1}+by_{1}+c}{b}\right)\frac{b}{\sqrt{a^2+b^2}}$$
$$d=\left(\frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right)$$
Nota: El signo de valor absoluto es dado al resultado, ya que en esta demostración asumimos que la recta tiene pendiente negativa y que el punto P se encuentra arriba de la recta. Si es que el punto P hubiera esta debajo de la recta, habríamos introducido un signo negativo en la fórmula.
Distancia de un punto a una recta – Ejercicios resueltos
Los siguientes ejercicios son resueltos usando la fórmula de la distancia de un punto a una recta. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo.
EJERCICIO 1
Encuentra la distancia desde el punto (2, 3) hasta la recta $latex x+y+2=0$
Solución
Tenemos que usar la fórmula de la distancia con los siguientes valores:
- x1 = 2
- y1 = 3
- a = 1
- b = 1
- c = 2
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(1)(2)+(1)(3)+2}{\sqrt{1^2+1^2}}\right|$$
$$=\left| \frac{2+3+2}{\sqrt{1+1}}\right|$$
$$=\left| \frac{7}{\sqrt{2}}\right|=\frac{7\sqrt{2}}{2}$$
$latex \approx 4.95$
La distancia desde el punto hasta la recta es 4.95 unidades.
EJERCICIO 2
Determina la distancia desde el punto (5, 5) hasta la recta $latex 2x-y+3=0$.
Solución
Empezamos reconociendo los siguientes valores:
- x1 = 5
- y1 = 5
- a = 2
- b = -1
- c = 3
Ahora, usamos a estos valores en la fórmula de la distancia:
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(2)(5)+(-1)(5)+3}{\sqrt{2^2+(-1)^2}}\right|$$
$$=\left| \frac{10-5+3}{\sqrt{4+1}}\right|$$
$$=\left| \frac{8}{\sqrt{5}}\right|=\frac{8\sqrt{5}}{5}$$
$latex \approx 3.578$
La distancia desde el punto hasta la recta es 3.578 unidades.
EJERCICIO 3
¿Cuál es la distancia desde el punto (-2, 5) hasta la recta $latex -2x+3y+4=0$?
Solución
Los valores dados son siguientes:
- x1 = -2
- y1 = 5
- a = -2
- b = 3
- c = 4
Aplicando la fórmula de la distancia con estos valores, tenemos:
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-2)(-2)+(3)(5)+4}{\sqrt{(-2)^2+3^2}}\right|$$
$$=\left| \frac{4+8+4}{\sqrt{4+9}}\right|$$
$$=\left| \frac{16}{\sqrt{13}}\right|=\frac{16\sqrt{13}}{13}$$
$latex \approx 4.438$
La distancia desde el punto hasta la recta es 4.438 unidades.
EJERCICIO 4
Determina la distancia desde el punto (3, -2) hasta la recta $latex -3x-2y-4=0$
Solución
Aplicamos la fórmula de la distancia vista arriba con los siguientes valores:
- x1 = 3
- y1 = -2
- a = -3
- b = -2
- c = -4
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-3)(3)+(-2)(-2)-4}{\sqrt{(-3)^2+(-2)^2}}\right|$$
$$=\left| \frac{-9+4-4}{\sqrt{9+4}}\right|$$
$$=\left| \frac{-9}{\sqrt{13}}\right|=\frac{9\sqrt{13}}{13}$$
$latex \approx 2.496$
La distancia desde el punto hasta la recta es 2.496 unidades.
EJERCICIO 5
Encuentra la distancia desde el punto (-2, 4) hasta la recta $latex -2x+5y-2=0$
Solución
Tenemos que usar la fórmula que aprendimos usando los siguientes valores:
- x1 = -2
- y1 = 4
- a = -2
- b = 5
- c = -2
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-2)(-2)+(5)(4)-2}{\sqrt{(-2)^2+5^2}}\right|$$
$$=\left| \frac{4+20-2}{\sqrt{4+25}}\right|$$
$$=\left| \frac{22}{\sqrt{29}}\right|=\frac{22\sqrt{29}}{29}$$
$latex \approx 4.085$
La distancia desde el punto hasta la recta es 4.085 unidades.
EJERCICIO 6
¿Cuál es la distancia desde el punto (0, 3) hasta la recta $latex -5x+2y+10=0$?
Solución
Tenemos que usar la fórmula de la distancia con los siguientes valores:
- x1 = 0
- y1 = 3
- a = -5
- b = 2
- c = 10
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(-5)(0)+(2)(3)+10}{\sqrt{(-5)^2+2^2}}\right|$$
$$=\left| \frac{0+6+10}{\sqrt{25+4}}\right|$$
$$=\left| \frac{16}{\sqrt{29}}\right|=\frac{16\sqrt{29}}{29}$$
$latex \approx 2.971$
La distancia desde el punto hasta la recta es 2.971 unidades.
EJERCICIO 7
Determina la distancia desde el punto (-4, 4) hasta la recta $latex 3x+10y-5=0$.
Solución
Vamos a usar la fórmula de la distancia perpendicular de un punto a una recta con los siguientes valores:
- x1 = -4
- y1 = 4
- a = 3
- b = 10
- c = -5
$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$
$$=\left| \frac{(3)(-4)+(10)(4)-5}{\sqrt{3^2+10^2}}\right|$$
$$=\left| \frac{-12+40-5}{\sqrt{9+100}}\right|$$
$$=\left| \frac{23}{\sqrt{109}}\right|=\frac{23\sqrt{109}}{109}$$
$latex \approx 2.203$
La distancia desde el punto hasta la recta es 2.203 unidades.
Distancia desde un punto a una recta – Ejercicios para resolver
Intenta resolver los siguientes ejercicios aplicando la fórmula de la distancia desde un punto a una recta. Haz clic en «Verificar» para comprobar que la respuesta seleccionada es correcta.
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
