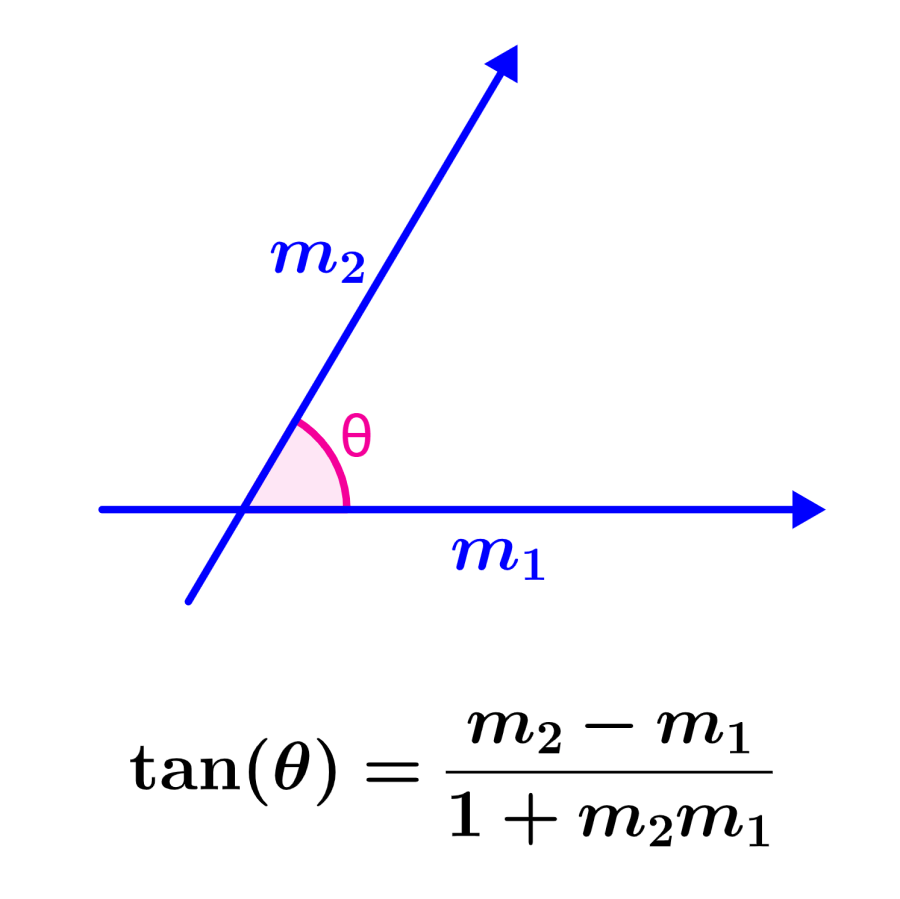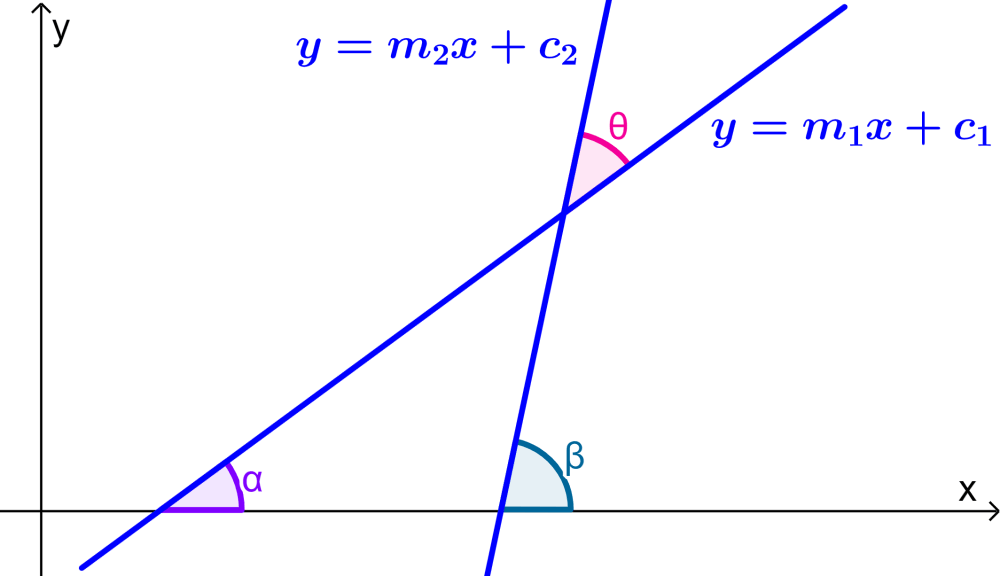El ángulo entre dos rectas nos permite determinar la inclinación que existe entre las rectas. Podemos calcular el ángulo entre dos líneas rectas usando una fórmula general que usa las pendientes de ambas líneas. Esta fórmula puede ser derivada usando trigonometría.
A continuación, aprenderemos cómo usar las pendientes de dos rectas para encontrar el ángulo que se ubica entre ellas. Usaremos la fórmula general para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a encontrar el ángulo entre dos rectas con ejercicios.
GEOMETRÍA
Relevante para…
Aprender a encontrar el ángulo entre dos rectas con ejercicios.
Fórmula del ángulo entre dos rectas
Si es que tenemos las dos rectas $latex y=m_{1}x+c_{1}$ y $latex y=m_{2}x+c_{2}$, el ángulo entre las rectas está dado por la siguiente fórmula:
| $$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$ |
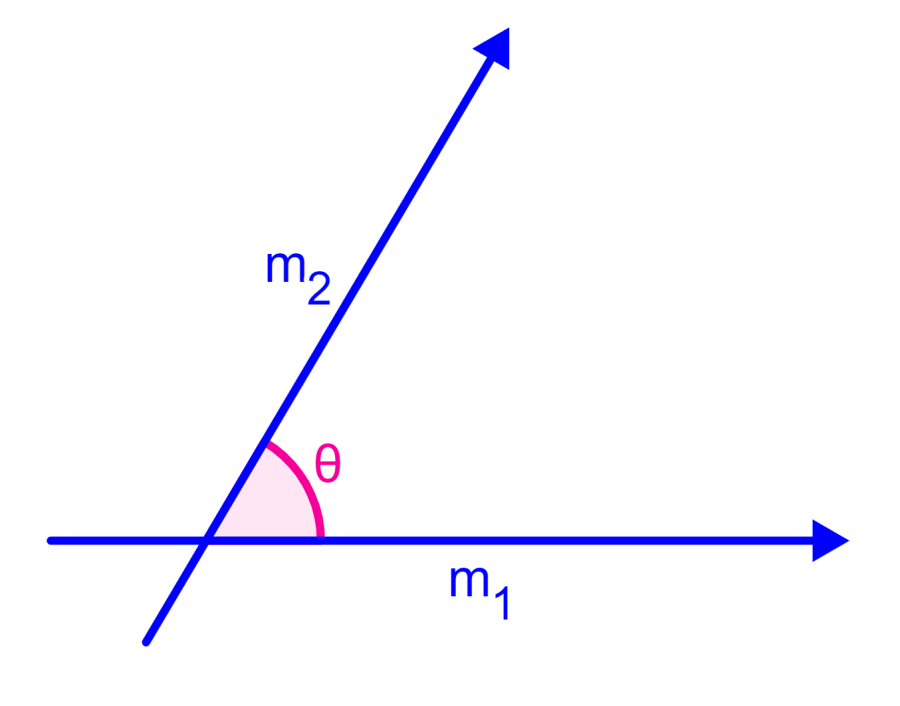
en donde, θ es el ángulo entre las rectas, $latex m_{1}$ es la pendiente de la primera recta y $latex m_{2}$ es la pendiente de la segunda recta como se muestra en el siguiente diagrama:
Puedes escoger a las pendientes en el orden que sea. Entonces, $latex m_{2}$ puede ser mayor que o menor que $latex m_{1}$.
Demostración de la fórmula del ángulo entre dos rectas
Para demostrar la fórmula del ángulo entre dos rectas, vamos a usar trigonometría junto con el siguiente diagrama:
Aquí, tenemos las rectas $latex y=m_{1}x+c_{1}$ y $latex y=m_{2}x+c_{2}$, las cuales forman los ángulos α y β con el eje x respectivamente.
Usando teoremas de ángulos, podemos determinar que $latex \theta = \beta – \alpha$. Entonces, tenemos lo siguiente:
$latex \tan(\theta)=\tan(\beta -\alpha)$
Usando la fórmula de Identidades de Suma y Resta de Ángulos para la tangente, tenemos:
$$\tan(\theta)=\frac{\tan(\beta)-\tan(\alpha)}{1+\tan(\beta)\tan(\alpha)}$$
Ahora, podemos escribir $latex \tan(\beta)=m_{2}$ y $latex \tan(\alpha)=m_{1}$, ya que estas son las pendientes de las rectas. Entonces, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
Ángulo entre dos rectas – Ejercicios resueltos
Los siguientes ejercicios son resueltos usando la fórmula del ángulo entre dos rectas. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios antes de mirar la respuesta.
EJERCICIO 1
Encuentra el ángulo entre las rectas $latex y=x$ y $latex y=3x-4$.
Solución
Recordemos que en la forma $latex y=mx+b$, m es la pendiente de la recta. Entonces, tenemos:
- La recta $latex y=x$ tiene una pendiente de 1, por lo que $latex m_{1}=1$
- La recta $latex y=3x-4$ tiene una pendiente de 3, por lo que $latex m_{2}=3$
Usando la fórmula del ángulo entre dos rectas, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{3-1}{1+(3)(1)}$$
$$\tan(\theta)=\frac{2}{4}$$
$$\tan(\theta)=\frac{1}{2}$$
$$\theta=\tan^{-1}\left(\frac{1}{2}\right)$$
$$\theta=26.6^{\circ}$$
EJERCICIO 2
¿Cuál es el ángulo entre las rectas $latex y=2x-5$ y $latex y=5x+6$?
Solución
Tenemos lo siguiente:
- La recta $latex y=2x-5$ tiene una pendiente de 2, por lo que $latex m_{1}=2$
- La recta $latex y=5x+6$ tiene una pendiente de 5, por lo que $latex m_{2}=5$
Al aplicar la fórmula del ángulo entre dos rectas, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{5-2}{1+(5)(2)}$$
$$\tan(\theta)=\frac{3}{11}$$
$$\theta=\tan^{-1}\left(\frac{3}{11}\right)$$
$$\theta=15.26^{\circ}$$
EJERCICIO 3
Encuentra el ángulo entre las rectas $latex y=3+x$ y $latex y=6+2x$.
Solución
Podemos obtener la siguiente información:
- La recta $latex y=3+x$ tiene una pendiente de 1, por lo que $latex m_{1}=1$
- La recta $latex y=6+2x$ tiene una pendiente de 2, por lo que $latex m_{2}=2$
Usando la fórmula del ángulo entre dos rectas, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{2-1}{1+(2)(1)}$$
$$\tan(\theta)=\frac{1}{3}$$
$$\theta=\tan^{-1}\left(\frac{1}{3}\right)$$
$$\theta=18.43^{\circ}$$
EJERCICIO 4
Determina el ángulo entre las rectas $latex y=6x-7$ y $latex y=2-x$.
Solución
Tenemos lo siguiente:
- La recta $latex y=6x-7$ tiene una pendiente de 6, por lo que $latex m_{1}=6$
- La recta $latex y=2-x$ tiene una pendiente de -1, por lo que $latex m_{2}=-1$
Usando la fórmula con estos valores, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-1-6}{1+(-1)(6)}$$
$$\tan(\theta)=\frac{-7}{-5}$$
$$\tan(\theta)=\frac{7}{5}$$
$$\theta=\tan^{-1}\left(\frac{7}{5}\right)$$
$$\theta=54.46^{\circ}$$
EJERCICIO 5
¿Cuál es el ángulo que se encuentra entre las rectas $latex y=2x+3$ y $latex y=5-2x$.
Solución
Podemos obtener la siguiente información:
- La recta $latex y=2x+3$ tiene una pendiente de 2, por lo que $latex m_{1}=2$
- La recta $latex y=5-2x$ tiene una pendiente de -2, por lo que $latex m_{2}=-2$
Al aplicar la fórmula con estos valores, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2-2}{1+(-2)(2)}$$
$$\tan(\theta)=\frac{-4}{-3}$$
$$\theta=\tan^{-1}\left(\frac{4}{3}\right)$$
$$\theta=53.13^{\circ}$$
EJERCICIO 6
Encuentra el ángulo entre las rectas $latex y=4-2x$ y $latex y=9-3x$
Solución
Tenemos lo siguiente:
- La recta $latex y=4-2x$ tiene una pendiente de -2, por lo que $latex m_{1}=-2$
- La recta $latex y=9-3x$ tiene una pendiente de -3, por lo que $latex m_{2}=-3$
Usando la fórmula del ángulo entre dos rectas, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-3-(-2)}{1+(-3)(-2)}$$
$$\tan(\theta)=\frac{-1}{7}$$
$$\theta=\tan^{-1}\left(-\frac{1}{7}\right)$$
$$\theta=8.13^{\circ}$$
EJERCICIO 7
Encuentra el ángulo entre las rectas $latex y=4$ y $latex 3y+2x-6=0$.
Solución
Tenemos lo siguiente:
- La recta $latex y=4$ es horizontal y tiene una pendiente de 0, por lo que $latex m_{1}=0$
- La recta $latex 3y+2x-6=0$ puede ser escrita como $latex y=-2/3x+2$, por lo que tiene una pendiente de -2/3, $latex m_{2}=-2/3$
Usando la fórmula del ángulo entre dos rectas, tenemos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2/3}{1+(-2/3)(0)}$$
$$\tan(\theta)=\frac{-2/3}{1}$$
$$\tan(\theta)=-\frac{2}{3}$$
$$\theta=\tan^{-1}\left(-\frac{2}{3}\right)$$
$$\theta=33.69^{\circ}$$
Ángulo entre dos rectas – Ejercicios para resolver
Aplica la fórmula del ángulo entre dos rectas para resolver los siguientes ejercicios. Si tienes problemas con esto, puedes usar los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
