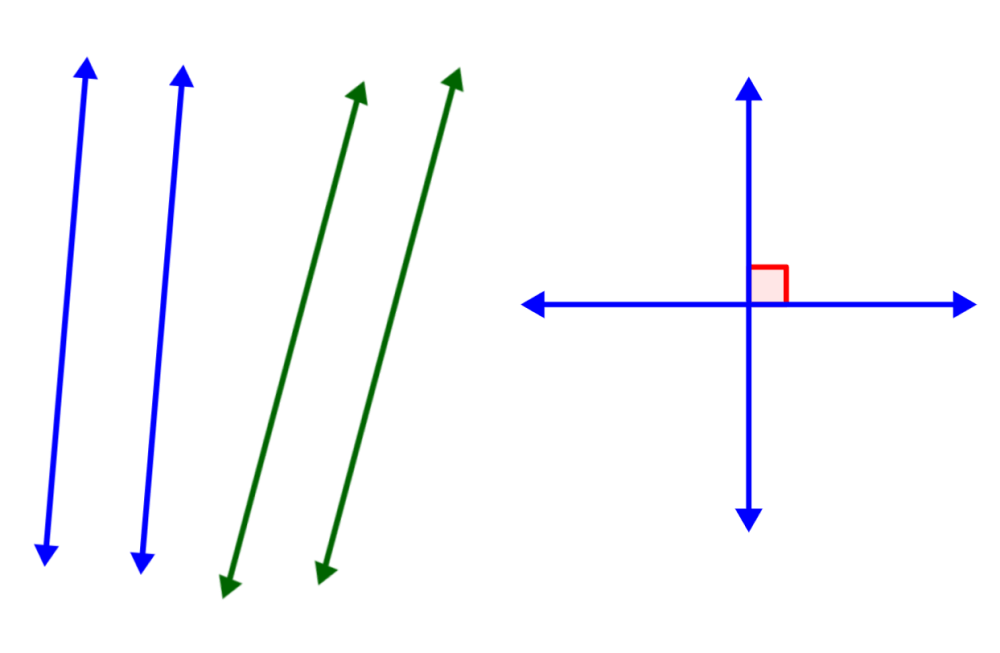
Las rectas paralelas son rectas que tienen la misma pendiente. Estas rectas nunca se cruzan sin importar cuánto sean extendidas. Por otro lado, las rectas perpendiculares son dos rectas que intersecan a un ángulo de 90° la una con la otra. Las pendientes de estas rectas son recíprocos negativos la una de la otra.
A continuación, aprenderemos todo lo relacionado con las rectas paralelas y perpendiculares. Veremos sus definiciones, algunas características importantes y algunos ejemplos.
Definiciones de las rectas paralelas y rectas perpendiculares
¿Qué son las rectas paralelas?
Las rectas paralelas son dos o más rectas que se ubican en el mismo plano cartesiano y que nunca intersecan la una con la otra. Sin importar qué tan largo extendamos a dos rectas paralelas, nunca se tocarán.
El siguiente es un diagrama con dos pares de rectas paralelas.
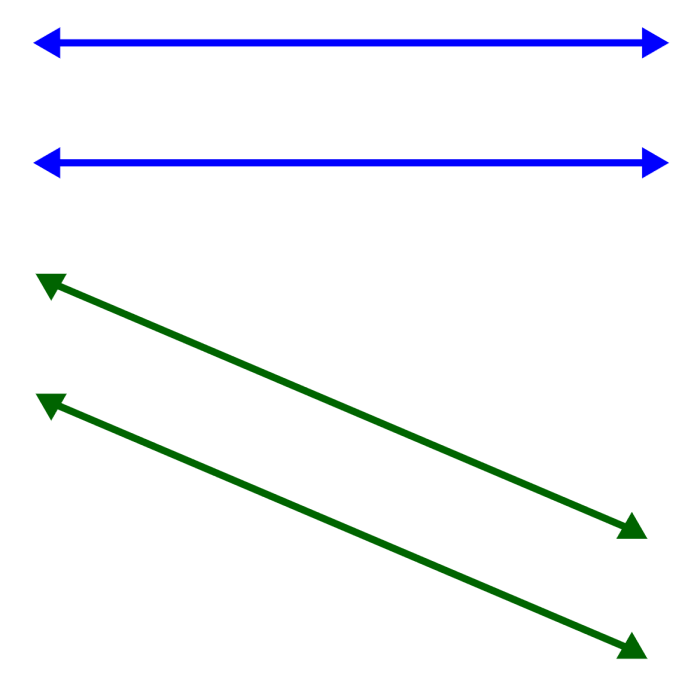
La característica principal de dos o más rectas paralelas es que tienen la misma pendiente. Es decir, el ángulo de inclinación de las rectas paralelas es el mismo.
¿Qué son las rectas perpendiculares?
Las rectas perpendiculares son dos rectas que intersecan la una con la otra en un ángulo de 90°. Es decir, las rectas perpendiculares forman un ángulo recto en su punto de intersección.
El siguiente es un diagrama de dos rectas perpendiculares.
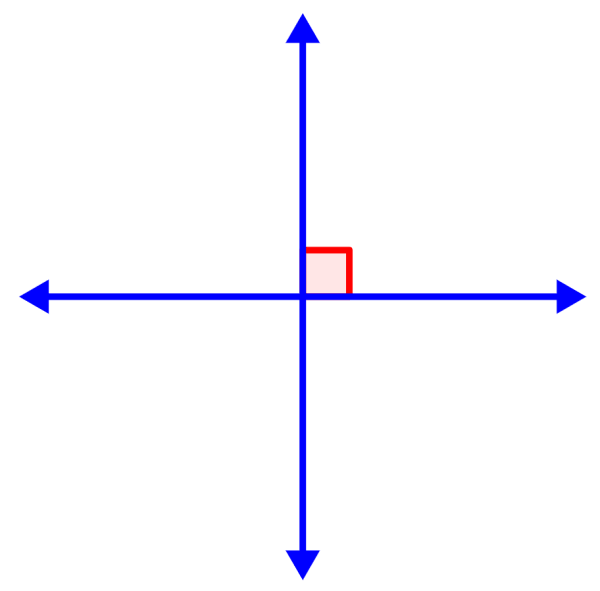
Propiedades de las rectas paralelas y perpendiculares
Las rectas paralelas pueden ser identificadas porque tienen la misma inclinación y nunca se tocan. Por otro lado, las rectas perpendiculares pueden ser identificadas porque forman una intersección con forma de «L».
Las siguientes son algunas propiedades importantes de las rectas paralelas:
- Las rectas paralelas nunca se intersecan la una con la otra.
- La distancia entre dos rectas paralelas siempre se mantiene constante.
- Las pendientes de las rectas paralelas son las mismas.
Las siguientes son algunas propiedades importantes de las rectas perpendiculares:
- Las rectas perpendiculares siempre intersecan la una con la otra.
- El ángulo de intersección entre dos rectas perpendiculares siempre es 90°.
- Las pendientes de las rectas perpendiculares son recíprocas y negativas la una de la otra. Es decir, tenemos $latex m_{1}=-\frac{1}{m_{2}}$.
- Si es que una recta es perpendicular a una recta que es paralela con otras rectas, entonces, la recta es perpendicular a todas las otras rectas.
¿Cómo determinar si dos rectas son paralelas o perpendiculares?
Podemos determinar si dos rectas son paralelas o perpendiculares usando los ángulos formados entre las rectas o usando sus pendientes.
Usar los ángulos formados
Para que dos rectas sean perpendiculares, el ángulo de intersección debe ser igual a 90°. Por otro lado, para que las rectas sean paralelas, el ángulo formado por las rectas con respecto a la horizontal, deben ser iguales.
Usar las pendientes de las rectas
Para que dos rectas sean paralelas, sus pendientes deben ser las mismas. Por otro lado, para que dos rectas sean perpendiculares, sus rectas deben ser recíprocas negativas la una de la otra.
Es decir, para dos rectas que tienen las pendientes $latex m_{1}$ y $latex m_{2}$, tenemos:
Paralelas: $latex m_{1}=m_{2}$
Perpendiculares: $latex m_{1}=-\frac{1}{m_{2}}$
Recordemos que en la ecuación de una recta $latex y=mx+b$, m es la pendiente.
Además, si es que conocemos dos puntos en la recta, su pendiente es $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$, en donde, $latex (x_{1},~y_{1})$ y $latex (x_{2},~y_{2})$ son las coordenadas de los puntos.
Ejercicios resueltos de rectas paralelas y perpendiculares
Los siguientes son algunos ejercicios de aplicación de rectas paralelas y perpendiculares.
EJERCICIO 1
Si es que tenemos la recta $latex 8x-2y=10$, ¿cuál es la pendiente de una recta paralela?
Solución: Para que dos rectas sean paralelas, deben tener la misma pendiente. Entonces, tenemos que encontrar la pendiente de la recta dada.
Para esto, tenemos que escribir a la recta en la forma $latex y=mx+b$. Esto significa que resolvemos para y:
$latex 8x-2y=10$
$latex -2y=10-8x$
$latex y=4x-5$
La pendiente de la recta es $latex m=4$. Por lo tanto, la pendiente de la recta paralela también debe ser $latex m=4$.
EJERCICIO 2
En el siguiente diagrama, las rectas $latex l_{1}$ y $latex l_{2}$ son paralelas. Además, también tenemos al ángulo ∠a=25°. Encuentra la medida del ángulo b.
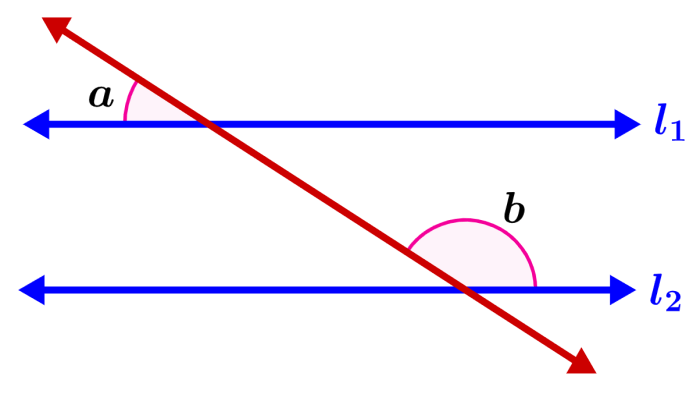
Solución: Las rectas son paralelas, por lo que su ángulo de inclinación es el mismo. Esto significa que la recta que corta a ambas paralelas, debe formar los mismos ángulos en ambas rectas.
Por lo tanto, podemos mover el ángulo a de la primera recta a la segunda. Entonces, los ángulos a y b son suplementarios, es decir, suman 180°. Entonces, tenemos:
∠b=180°-25°=155°
El ángulo b mide 155°.
EJERCICIO 3
La recta AB del siguiente diagrama es perpendicular a la recta CD. Determina el valor del ángulo x.
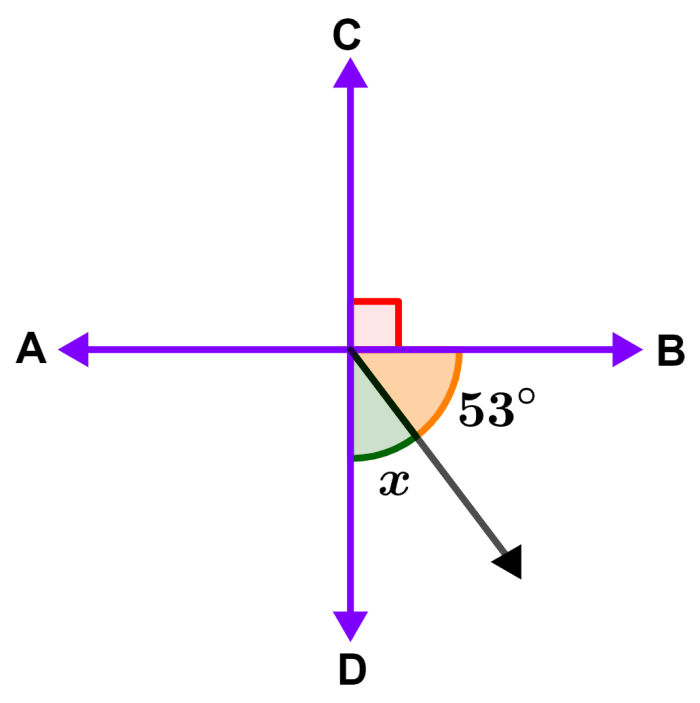
Solución: Las rectas perpendiculares forman ángulos de 90° en el punto de intersección. Entonces, los ángulos x y 53° deben sumar 90°. Formando una ecuación y resolviendo, tenemos:
$latex 53^{\circ}+x=90^{\circ}$
$latex x=90^{\circ}-53^{\circ}$
$latex x=37^{\circ}$
El ángulo x mide 37°.
EJERCICIO 4
Si es que una recta tiene la ecuación $latex 6x+3y=12$, encuentra la pendiente de una recta perpendicular.
Solución: Tenemos que empezar encontrando la pendiente de la recta dada. Para esto, escribimos a la recta en la forma $latex y=mx+b$:
$latex 6x+3y=12$
$latex 3y=-6x+12$
$latex y=-2x+4$
Vemos que la pendiente es $latex m_{1}=-2$.
Ahora, para encontrar la pendiente de la recta perpendicular, recordamos que rectas perpendiculares tienen pendientes que son recíprocos negativos la una de la otra.
Entonces, la pendiente de la recta perpendicular es $latex m_{2}=\frac{1}{2}$
Véase también
¿Interesado en aprender más sobre ángulos y rectas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
