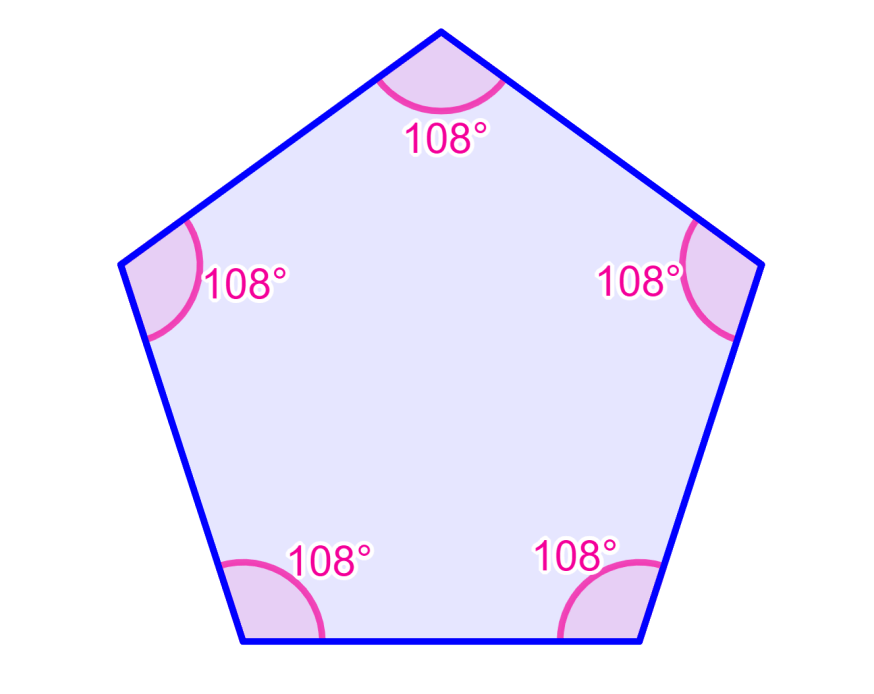
Los pentágonos tienen una suma de ángulos internos de 540°. Entonces, en el caso de pentágonos regulares, cada ángulo interno mide 108°. Los pentágonos irregulares tienen ángulos de diferentes medidas, pero su suma siempre es igual a 540°.
A continuación, conoceremos más detalles sobre los ángulos internos de un pentágono. Conoceremos la fórmula de ángulos internos y resolveremos algunos ejercicios.
Suma de ángulos internos de un pentágono
La suma de todos los ángulos internos de cualquier pentágono siempre es igual a 540°. Esto aplica sin importar si el pentágono es regular o irregular. Esta suma es obtenida al aplicar la fórmula de suma de ángulos de polígonos:
| $latex (n-2)\times 180$° |
en donde, n es el número de lados del polígono. En el caso de un pentágono, tenemos $latex n=5$. Entonces, usando la fórmula:
$latex (n-2)\times 180$°
$latex =(5-2)\times 180$°
$latex =(3)\times 180$°
$latex =540$°
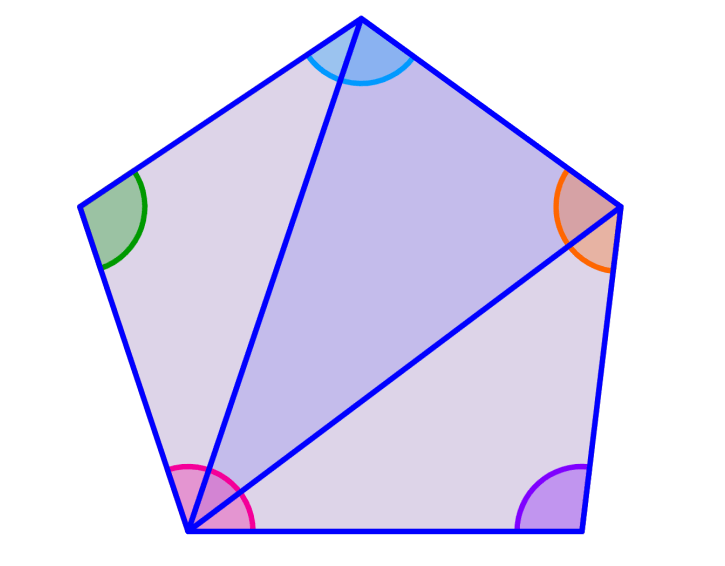
Por su parte, esta fórmula es derivada considerando que podemos dividir a cualquier polígono en triángulos como en el siguiente diagrama:
Para cualquier polígono, podemos formar un total de n-2 triángulos. Además, sabemos que cada triángulo tiene una suma de ángulos internos de 180°, por lo que $latex (n-2)\times 180$° corresponde a la suma de los ángulos internos del polígono.
Medida de un ángulo interno de pentágonos
Si es que el pentágono es regular, sabemos que todos sus lados tienen la misma medida. Entonces, podemos determinar las medidas de cada ángulo interno simplemente al dividir la suma total por 5. Entonces, tenemos:
540°÷5=108°
La medida de cada ángulo interno en un pentágono regular es igual a 108°.
En el caso de pentágonos irregulares, las medidas de sus ángulos internos son diferentes los unos con los otros. Entonces, para calcular la medida de algún ángulo faltante, necesitamos conocer las medidas de los otros ángulos.
Por ejemplo, si es que sabemos que un pentágono tiene los ángulos 110°, 100°, 120° y 90°, podemos calcular la medida del quinto ángulo al sumar los ángulos conocidos y restar de 540°. Entonces, tenemos:
110°+100°+120°+90°=420°
⇒ 540°-420°=120°
La medida del ángulo faltante es 120°.
Ejemplos resueltos de ángulos internos de un pentágono
EJEMPLO 1
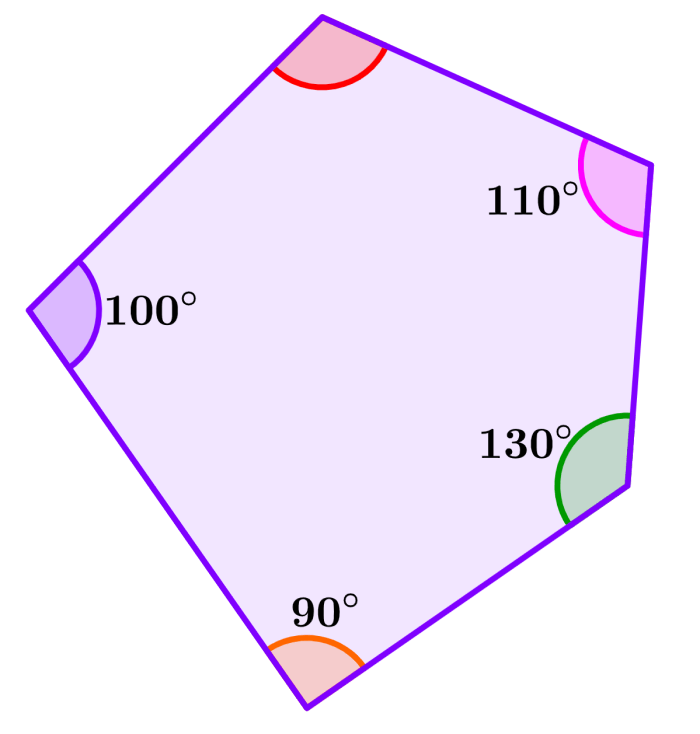
Encuentra los ángulos faltantes en el siguiente pentágono.
Solución: En este caso, tenemos los ángulos 90°, 100°, 130° y 110°. Entonces, empezamos sumándolos:
90°+100°+130°+110°=430°
Ahora, restamos esto de 540° para encontrar el ángulo faltante:
540°-430°=110°
El ángulo faltante mide 110°.
EJEMPLO 2
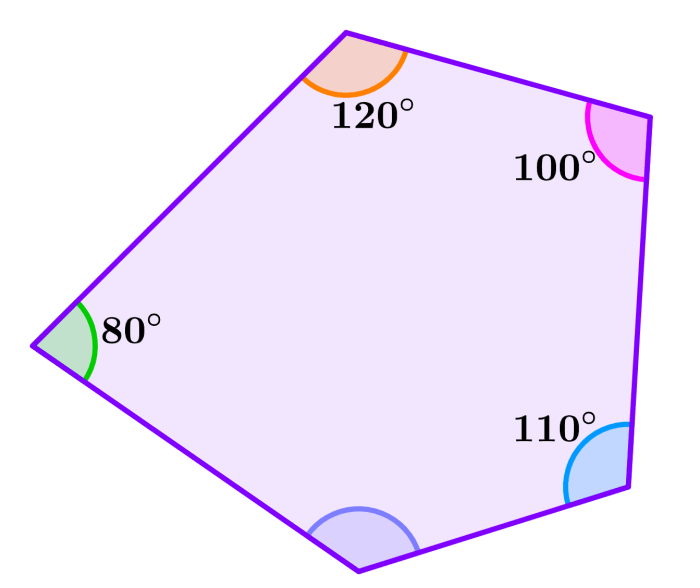
Determina la medida del ángulo faltante en el siguiente pentágono.
Solución: Sabemos que la suma de todos los ángulos internos de un pentágono es igual a 540°. Entonces, tenemos que sumar todos los ángulos conocidos y restar de 540°:
80°+120°+100°+110°=410°
⇒ 540°-410°=130°
La medida del ángulo faltante es 130°.
EJEMPLO 3
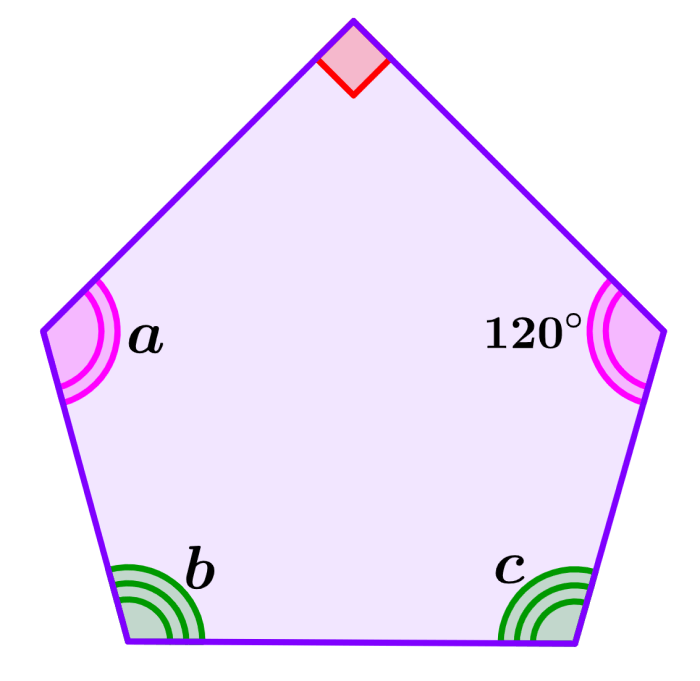
Ahora, veamos un ejemplo en el que tenemos que encontrar más de un ángulo faltante. Aquí, los ángulos que son diferentes están señalados de forma diferente.
Solución: Dado que los ángulos que tienen doble línea son iguales, tenemos a=120°.
Además, también sabemos que los ángulos b y c son iguales, ya que ambos tienen triple línea. Para encontrar la medida de estos ángulos, empezamos sumando los ángulos que conocemos hasta ahora:
90°+120°+120°=330°
Ahora, restamos esto de 540° para encontrar los ángulos faltantes:
540°-330°=210°
Dado que los dos ángulos faltantes son iguales, dividimos 210° por 2 para obtener la medida de cada uno. Entonces, tenemos b=105° y c=105°.
EJEMPLO 4
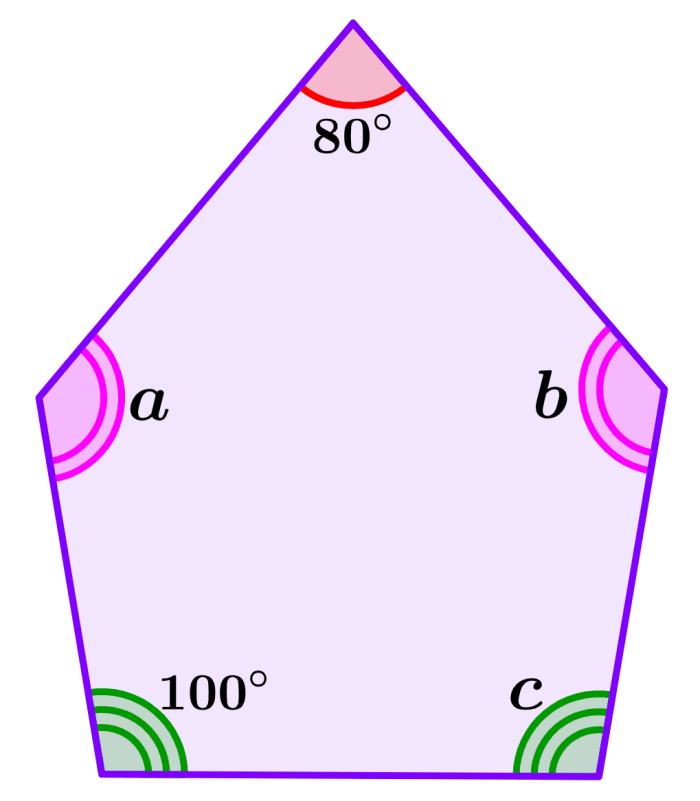
Encuentra los ángulos faltantes en el siguiente pentágono.
Solución: Los ángulos que tienen triple línea tienen la misma medida. Entonces, tenemos c=100°.
Los ángulos a y b también tienen la misma medida, ya que ambos tienen doble línea. Para encontrar su medida, tenemos que empezar sumando los ángulos conocidos:
80°+100°+100°=280°
Ahora, restamos esto de 540° y tenemos:
540°-280°=260°
Dado que los ángulos a y b son los mismos, dividimos el resultado para 2 y tenemos a=130° y b=130°.
Véase también
¿Interesado en aprender más sobre ángulos internos de polígonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
