Los heptágonos tienen una suma de ángulos internos de 900°. En un heptágono regular, todos los lados tienen la misma longitud, por lo que los ángulos internos también tienen la misma medida. Entonces, cada ángulo interno de un heptágono mide 120°. Sin embargo, un hexágono irregular tiene ángulos internos diferentes, pero siempre tienen una suma total igual a 900°.
A continuación, conocemos más detalles sobre los ángulos internos de heptágonos. Aprenderemos sobre su fórmula y resolveremos algunos ejercicios.
Ángulos internos en un heptágono regular
Los heptágonos regulares se caracterizan por tener lados con la misma longitud, es decir, todos los lados de un heptágono regular son congruentes. Además, los heptágonos regulares también tienen ángulos internos con la misma medida.
Cuando sumamos todos los ángulos internos de cualquier heptágono, siempre obtenemos 900°. Entonces, para determinar la medida de un ángulo interno de un heptágono regular, dividimos 900° por 7 y tenemos:
900°÷7≈128.571°
Cada ángulo interno en un heptágono regular mide 128.571°.
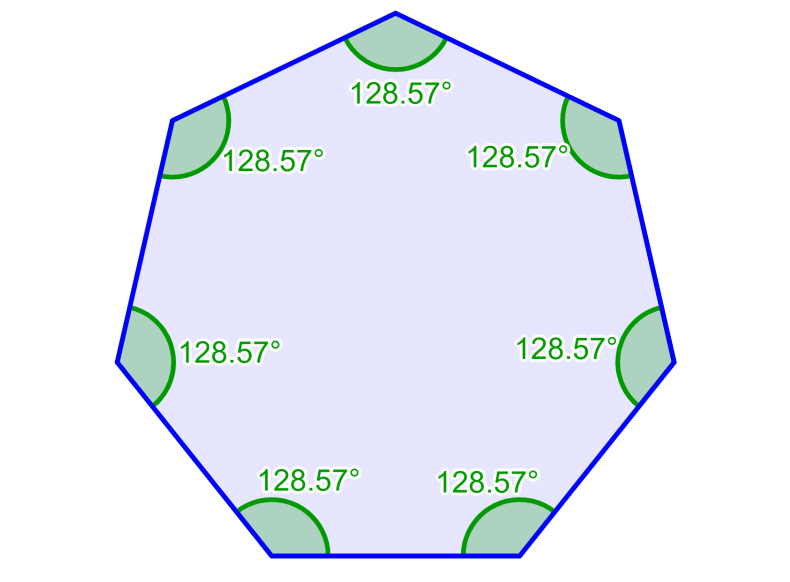
El siguiente diagrama es un ejemplo de un heptágono regular, el cual tiene lados con la misma longitud y ángulos con la misma medida. Cuando sumamos los siete ángulos de 128.571°, obtenemos un total de 900°.
Fórmula para encontrar los ángulos de un heptágono
La suma de los ángulos internos de cualquier polígono puede ser encontrada usando la siguiente fórmula:
| $latex (n-2)\times 180$° |
En esta fórmula, n representa al número de lados del polígono. En este caso, usamos $latex n=7$ para un heptágono. Sustituyendo este valor, tenemos $latex (5)\times 180=900$°. Esto demuestra que la suma de los ángulos internos de un heptágono es igual a 900°.
¿Cómo encontrar un ángulo faltante en un heptágono?
Sabemos que un heptágono regular tiene todos sus ángulos internos iguales con una medida de 128.571°. Sin embargo, en el caso de un ángulo faltante de un heptágono irregular, podemos determinarlo al sumar todas las medidas de los ángulos conocidos y restar el valor obtenido de 900°.
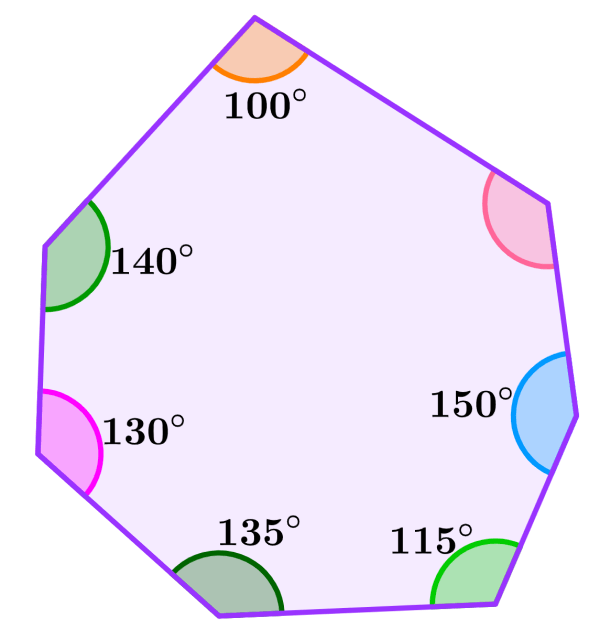
Por ejemplo, el siguiente es un heptágono irregular con los ángulos 100°, 140°, 130°, 135°, 115°, 150°.
Para encontrar la medida del ángulo faltante, empezamos sumando todos los ángulos conocidos:
100°, 140°, 130°, 135°, 115°, 150°=760°
Ahora, restamos el valor obtenido de 900°:
900°-760°=140°
Entonces, el ángulo faltante del heptágono tiene una medida de 140°.
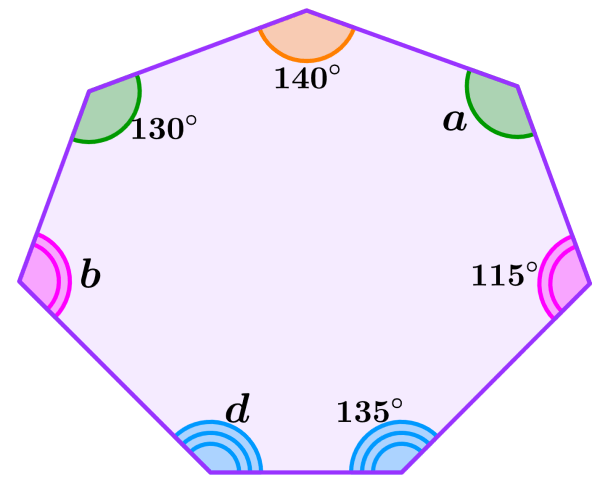
Ahora veamos un ejemplo en el que tenemos que encontrar más de un ángulo faltante. En este heptágono, los ángulos representados de la misma forma son iguales. Por ejemplo, los ángulos que tienen doble línea tienen la misma medida.
Dado que los ángulos que tienen una línea y son verdes son iguales, tenemos a=130°.
Los ángulos b y 115° también son iguales, ya que ambos están representados con doble línea y comparten el mismo color. Entonces, tenemos b=115°.
Finalmente, sabemos que el ángulo d es igual a 135°, ya que estos ángulos comparten el mismo color y tienen triple línea.
Ejemplos resueltos de ángulos internos de un heptágono
EJEMPLO 1
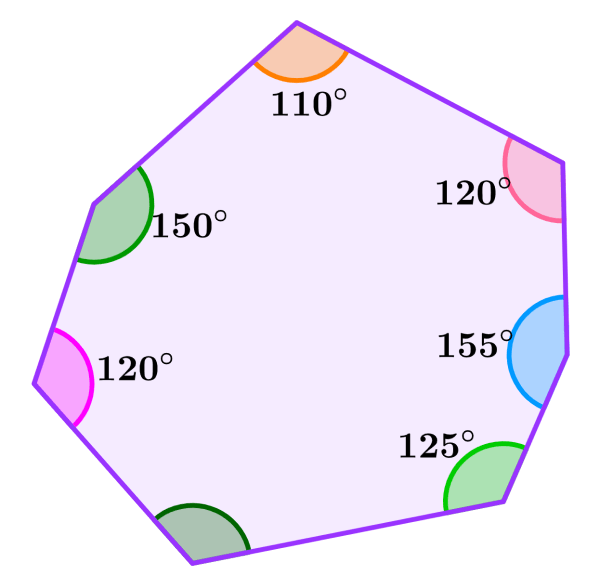
Encuentra la medida del ángulo faltante del heptágono.
Solución: Tenemos las medidas de los ángulos 110°, 150°, 120°, 125°, 155° y 120°. Entonces, sumamos estos ángulos:
110°+150°+120°+125°+155°+120°=780°
Ahora, encontramos el ángulo faltante al restar el valor obtenido de 900°:
900°-780°=120°
El ángulo faltante mide 120°.
EJEMPLO 2
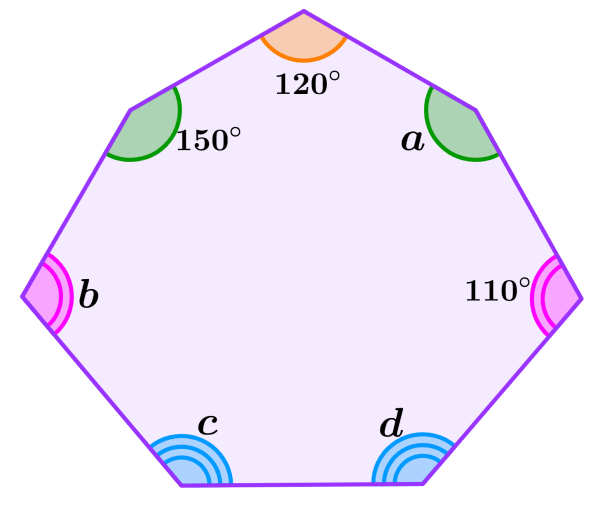
Determina las medidas de los ángulos faltantes en el siguiente heptágono.
Solución: Los ángulos representados con las dos líneas son iguales. Entonces, tenemos a=150°.
De igual forma, los ángulos b y 110° también son iguales, ya que ambos están representados con doble línea. Entonces, tenemos b=110°. Finalmente, podemos encontrar la medida de los ángulos c y d al empezar sumando los ángulos conocidos:
120°+150°+150°+110°+110°=640°
Ahora, restamos el valor obtenido de 900° y tenemos:
900°-640°=260°
Esto es igual a la suma de los dos ángulos faltantes. Dado que ambos ángulos son iguales, dividimos el resultado por 2 para obtener el valor de cada ángulo. Entonces, tenemos c=130° y d=130°.
Véase también
¿Interesado en aprender más sobre ángulos interiores de polígonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
