Calculadora de Seno (Grados y Radianes)
Respuesta:
Gráfica del seno
Con esta calculadora, puedes obtener el seno de cualquier ángulo ingresado. Al ingresar un ángulo, la calculadora mostrará el seno de ese ángulo inmediatamente. Es posible usar tanto grados como radianes.
A continuación, encontrarás información adicional con respecto al uso de la calculadora. Además, podrás conocer más sobre el coseno de un ángulo en general. Encontrarás la definición del seno, su gráfica y los valores del seno de ángulos importantes.
¿Cómo usar la calculadora de seno?
Paso 1: Haz clic en el botón azul para seleccionar el tipo de ángulo que vas a ingresar. Tienes la opción de usar grados, radianes o π radianes.
Paso 2: Ingresa el ángulo en la casilla «Ángulo». Es posible usar tanto números positivos como negativos.
Paso 3: El seno del ángulo será mostrado inmediatamente en el panel derecho.
Diferencia entre grados, radianes y π radianes en la calculadora
Un círculo completo tiene un total de 360°, lo cual es equivalente a 2π radianes. Entonces, podemos deducir que 180° son equivalentes a π radianes.
Ahora, recordando que π tiene un valor aproximado de 3.1415…, podemos deducir que π radianes es aproximadamente 3.1415 radianes. Entonces, dependiendo del ángulo que queremos ingresar, debemos seleccionar entre las tres opciones disponibles.
Por ejemplo, si es que queremos encontrar el seno del ángulo 60°, podemos realizar cualquiera de las tres opciones equivalentes:
- Podemos seleccionar «grados» e ingresar 60.
- Podemos seleccionar «π radianes» e ingresar 0.3333 (180° es igual a π radianes, por lo que 60° es igual a 1/3 π radianes).
- Podemos seleccionar «radianes» e ingresar 1.0472 (0.3333π radianes es igual a 1.0472 radianes).
¿Qué es el seno de un ángulo?
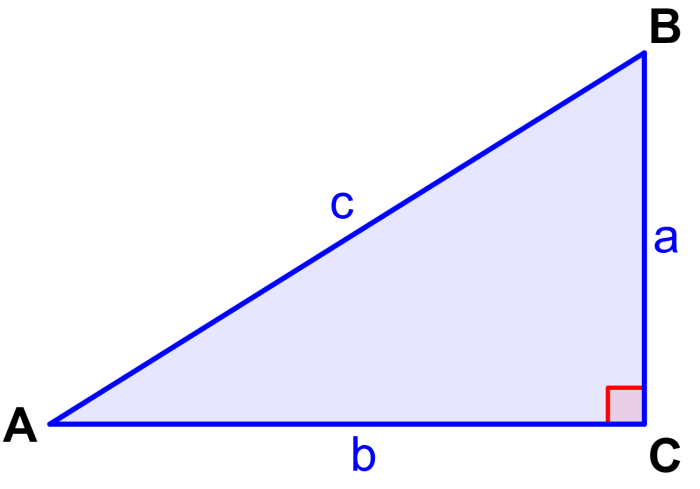
El seno es una de las funciones trigonométricas fundamentales junto con el coseno y la tangente. Podemos definir al seno de un ángulo usando un triángulo rectángulo. Entonces, el seno es igual a la longitud del lado opuesto al ángulo dividida por la longitud de la hipotenusa del triángulo.
Por ejemplo, usando el siguiente triángulo rectángulo, podemos definir al seno del ángulo A como la longitud del lado a (lado opuesto a A) dividida por la longitud del lado c (hipotenusa y opuesto al ángulo de 90°).
Además, podemos definir al seno del ángulo B como la longitud del lado b (lado opuesto a B) dividida por la longitud del lado c (hipotenusa).
Si quieres aprender más sobre el seno de un ángulo, visita nuestro artículo Seno de un Ángulo – Fórmulas y Ejercicios.
Gráfica del seno de un ángulo
El seno de un ángulo puede ser extendido para usar ángulos que están fuera de un triángulo rectángulo. Esto significa que la función seno puede tomar ángulos mayores de 180° tanto positivos como negativos.
La función seno es periódica, es decir, esta función se repite a sí misma después de un intervalo constante. En el caso del seno, su periodo es igual a 360° o 2π.
Dominio del seno de un ángulo
De la gráfica del seno, podemos deducir que cualquier valor puede ser usado como entrada. Es decir, podemos usar cualquier ángulo tanto positivo como negativo sin importar qué tan grande sea.
Por lo tanto, el dominio de la función seno es igual a todos los números reales.
Rango del seno de un ángulo
De la gráfica del seno, podemos concluir que los valores de salida van desde -1 hasta 1. La función seno no puede resultar en valores que sean mayores que 1, por lo que su rango es igual a -1 ≤ cos(α) ≤ 1.
Tabla del seno de ángulos comunes
| Grados | Radianes | Seno |
|---|---|---|
| -90° | -π/2 | -1 |
| -60° | -π/3 | -√3/2 |
| -45° | -π/4 | -√2/2 |
| -30° | -π/6 | -1/2 |
| 0° | 0 | 0 |
| 30° | π/6 | 1/2 |
| 45° | π/4 | √2/2 |
| 60° | π/3 | √3/2 |
| 90° | π/2 | 1 |
Calculadoras relacionadas:
- Calculadora de Coseno (Grados y Radianes)
- Calculadora de Tangente (Grados y Radianes)
- Calculadora de Secante (Grados y Radianes)
- Calculadora de Cosecante (Grados y Radianes)
- Calculadora de Cotangente (Grados y Radianes)
Puedes explorar otras calculadoras aquí.
