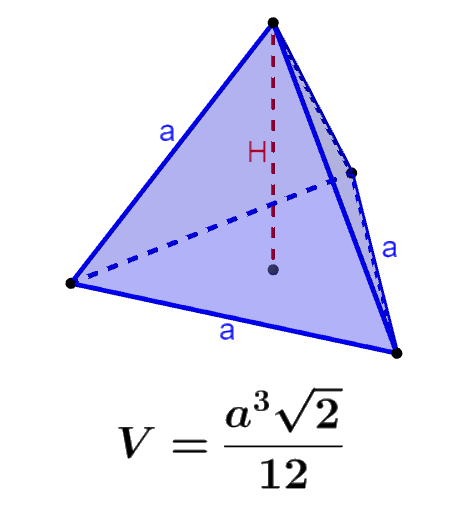
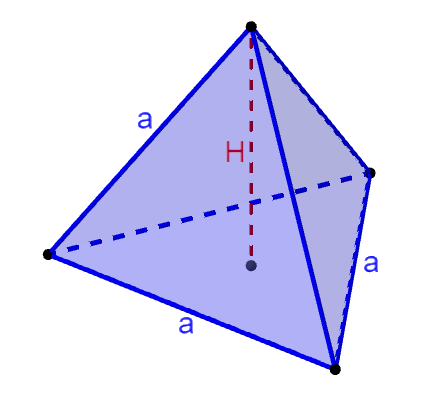
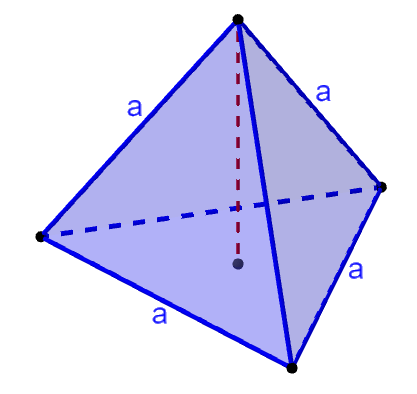
Un tetraedro es una pirámide regular que tiene cuatro caras triangulares. Esto significa que podemos calcular su volumen al multiplicar el área de su base por la altura del tetraedro y dividir por tres. Además, su área superficial es calculada al sumar las áreas de las cuatro caras triangulares.
A continuación, conoceremos las fórmulas para encontrar el volumen y el área superficial de un tetraedro. Aprenderemos a derivar estas fórmulas y las usaremos para resolver algunos ejercicios de práctica.
¿Cómo encontrar el volumen de un tetraedro?
Dado que el tetraedro es una pirámide triangular, podemos calcular su volumen al multiplicar el área de su base por la longitud de su altura y dividir por 3.
La fórmula del volumen de un tetraedro regular es:
| $latex V=\frac{{{a}^3}\sqrt{2}}{12}$ |
Demostración de la fórmula del volumen de un tetraedro
Como mencionamos anteriormente, los tetraedros son pirámides triangulares. Además, el área de cualquier pirámide puede ser calculada al multiplicar el área de su base por la altura de la pirámide y dividir por tres. Entonces, tenemos:
$latex V=\frac{1}{3}A_{b}H$
en donde, $latex A_{b}$ es el área de la base y H es la altura del tetraedro.
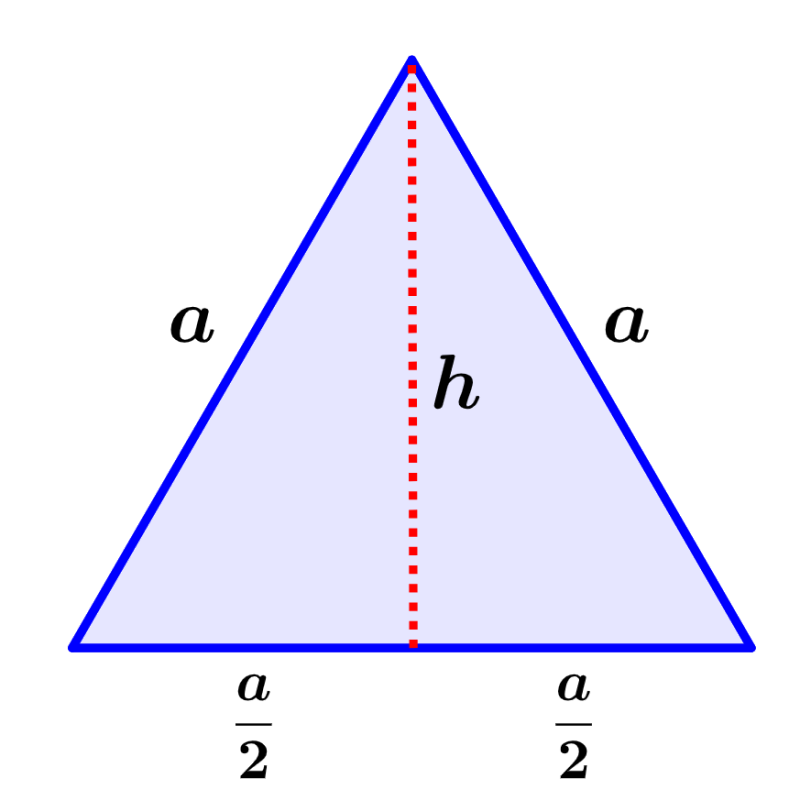
La base de un tetraedro es un triángulo equilátero y sabemos que el área de cualquier triángulo es igual a un medio de la base multiplicada por la altura. Entonces, tenemos:
$latex A_{b}=\frac{1}{2}bh$
La base del triángulo es igual a uno de los lados del tetraedro, a. Además, la altura de un triángulo equilátero es igual a $latex \frac{\sqrt{3}}{2}a$, en donde a es la longitud de uno de los lados. Entonces, tenemos
$latex A_{b}=\frac{1}{2}bh$
$latex A_{b}=\frac{1}{2}a\left( \frac{\sqrt{3}}{2}a\right)$
$latex A_{b}=\frac{\sqrt{3}}{4}{{a}^2}$
Finalmente, tenemos que la altura de un tetraedro es igual a:
$latex H=\frac{\sqrt{6}}{3}a$
Sustituyendo todo esto en la fórmula del volumen de un tetraedro, tenemos:
$latex V=\frac{1}{3}A_{b}H$
$latex V=\frac{1}{3}\left(\frac{1}{2}bh\right)\left(\frac{\sqrt{6}}{3}a\right)$
$latex V=\frac{{{a}^3}\sqrt{18}}{36}$
$latex V=\frac{{{a}^3}\sqrt{9\times 2}}{36}$
$latex V=\frac{3{{a}^3}\sqrt{2}}{36}$
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
¿Cómo encontrar el área superficial de un tetraedro?
Los tetraedros están formados de cuatro caras congruentes. Esto significa que podemos calcular su área superficial al sumar las áreas de las cuatro caras.
La fórmula del área superficial de un tetraedro regular es:
| $latex A_{s}=\sqrt{3} ~{{a}^2}$ |
Demostración de la fórmula del área superficial de un tetraedro
Dado que los tetraedros son pirámides triangulares, sus cuatro caras son congruentes. Esto significa que todas sus caras tienen la misma forma y la misma figura. Entonces, podemos calcular el área superficial si es que conocemos el área de una de las caras del tetraedro.
Esto significa que tenemos:
$latex A_{s}=4A_{t}$
en donde, $latex A_{s}$ es el área superficial del tetraedro y $latex A_{t}$ es el área de una de las caras triangulares.
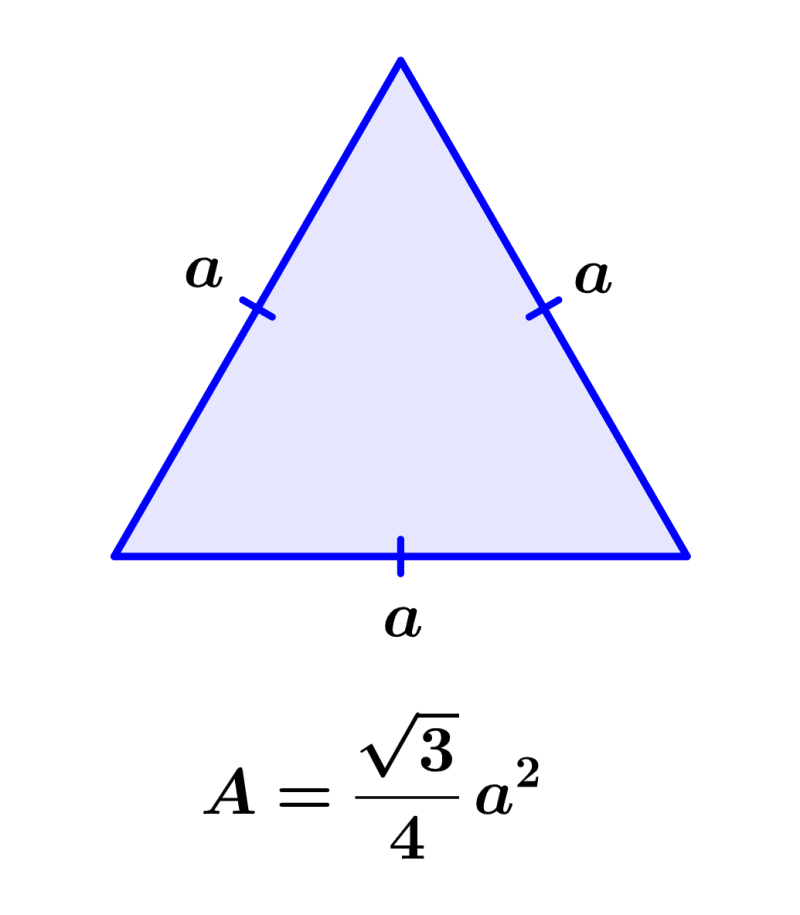
Ahora, podemos calcular el área de una de las caras al recordar que las caras de un tetraedro son triángulos equiláteros. Entonces, usamos la fórmula del área de un triángulo equilátero:
en donde, a es la longitud de uno de los lados.
Sustituyendo esto en la fórmula del área superficial del tetraedro, tenemos:
$latex A_{s}=4A_{t}$
$latex A_{s}=4\frac{\sqrt{3}}{4}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{a}^2}$
Volumen y área de un tetraedro – Ejercicios resueltos
EJERCICIO 1
Si es que un tetraedro tiene lados con una longitud de 3 m, ¿cuál es su volumen?
Solución
Para encontrar el volumen del tetraedro dado, simplemente podemos aplicar la fórmula del volumen sustituyendo a=3. Entonces, tenemos:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{3}^3}\sqrt{2}}{12}$
$latex V=\frac{9\sqrt{2}}{12}$
$latex V=1.06$
El volumen del tetraedro es $latex 1.06 {{m}^3}$.
EJERCICIO 2
¿Cuál es el área superficial de un tetraedro que tiene lados con una longitud de 5 m?
Solución
Vamos a usar la fórmula del área superficial dada arriba sustituyendo a=5. Entonces, tenemos:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{5}^2}$
$latex A_{s}=\sqrt{3}~25$
$latex A_{s}=43.3$
El área superficial del tetraedro es $latex 43.3 {{m}^2}$.
EJERCICIO 3
Un tetraedro tiene lados con una longitud de 20 cm. Calcula su volumen.
Solución
Tenemos que a=20. Entonces, usamos la fórmula del volumen de un tetraedro sustituyendo la longitud dada:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{20}^3}\sqrt{2}}{12}$
$latex V=\frac{8000\sqrt{2}}{12}$
$latex V=942.8$
El volumen del tetraedro es $latex 942.8 {{cm}^3}$.
EJERCICIO 4
Si es que un tetraedro tiene lados con una longitud de 6 m, ¿cuál es su área superficial?
Solución
Usando a=6 en la fórmula del área superficial, tenemos:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{6}^2}$
$latex A_{s}=\sqrt{3}~36$
$latex A_{s}=62.35$
El área superficial del tetraedro es $latex 62.35 {{m}^2}$.
EJERCICIO 5
¿Cuál es el volumen de un tetraedro que tiene lados con una longitud de 10 m?
Solución
Usamos la fórmula del volumen sustituyendo el valor de la longitud de los lados. Entonces, tenemos:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{10}^3}\sqrt{2}}{12}$
$latex V=\frac{1000\sqrt{2}}{12}$
$latex V=117.9$
El volumen del tetraedro es $latex 117.9 {{m}^3}$.
EJERCICIO 6
¿Cuál es el área superficial de un tetraedro que tiene lados con una longitud de 12 cm?
Solución
Usando la fórmula del área superficial con a=12, tenemos:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{12}^2}$
$latex A_{s}=\sqrt{3}~144$
$latex A_{s}=249.4$
El área superficial del tetraedro es $latex 249.4 {{m}^2}$.
EJERCICIO 7
Si es que el volumen de un tetraedro es igual a $latex 1000 {{m}^3}$, ¿cuál es la longitud de sus lados?
Solución
En este caso, tenemos el valor del volumen y queremos obtener la longitud de uno de sus lados. Entonces, podemos usar la fórmula del volumen del tetraedro y resolver para a:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 1000=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 12000={{a}^3}\sqrt{2}$
$latex 12000={{a}^3}\sqrt{2}$
$latex 8485.3={{a}^3}$
$latex a=20.4$
Entonces, los lados del tetraedro miden 20.4 m.
EJERCICIO 8
Si es que el área superficial de un tetraedro es igual a $latex 300 {{m}^2}$, ¿cuál es la longitud de sus lados?
Solución
En este caso, tenemos que encontrar la longitud de uno de los lados del tetraedro. Entonces, podemos usar la fórmula del área superficial y resolver para a:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex 300=\sqrt{3}~{{a}^2}$
$latex 173.2={{a}^2}$
$latex a=13.16$
La longitud de uno de los lados del tetraedro es 16.16 m.
EJERCICIO 9
El volumen de un tetraedro es igual a $latex 400 {{m}^3}$. ¿Cuál es la longitud de sus lados?
Solución
Similar al problema anterior, vamos a usar la fórmula del volumen de un tetraedro y luego resolveremos para a:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 400=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 4800={{a}^3}\sqrt{2}$
$latex 4800={{a}^3}\sqrt{2}$
$latex 3394.1={{a}^3}$
$latex a=15.03$
Entonces, los lados del tetraedro miden 15.03 m.
EJERCICIO 10
Si es que el área superficial de un tetraedro es igual a $latex 1000 {{m}^2}$, ¿cuál es la longitud de sus lados?
Solución
Nuevamente, usamos la fórmula del área superficial y resolvemos para a. Entonces, tenemos:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex 1000=\sqrt{3}~{{a}^2}$
$latex 577.35={{a}^2}$
$latex a=24.03$
La longitud de los lados del tetraedro es 24.03 m.
Volumen y área de un tetraedro – Ejercicios para resolver
El área superficial de un tetraedro es igual a 180.2 m2, ¿cuál es la longitud de sus lados?
Escribe la respuesta a un lugar decimal.
Véase también
¿Interesado en aprender más sobre tetraedros? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
