Las redes geométricas son formadas cuando extendemos a una figura 3D. En general, una red geométrica puede ser definida como una figura bidimensional que puede ser modificada para formar una figura tridimensional.
A continuación, conoceremos las redes geométricas de cubos, conos, cilindros, tetraedros y octaedros. Además, conoceremos algunas de sus características importantes.
Redes geométricas de un cubo
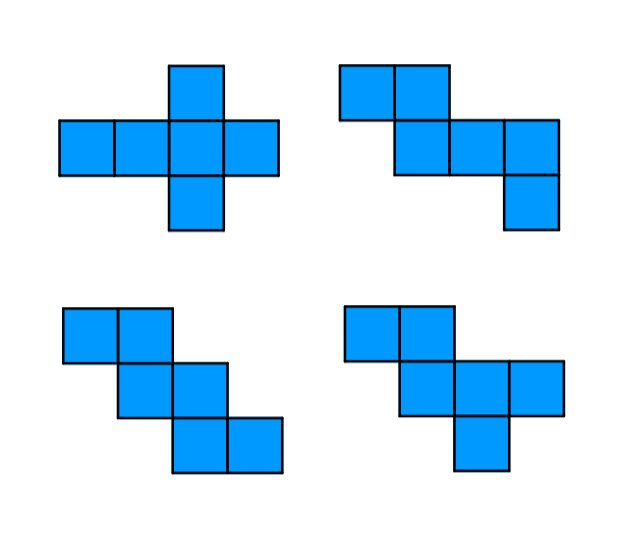
Un cubo es un poliedro regular de seis caras. Esto significa que todas las caras de un cubo son cuadrados. La siguiente es la red geométrica de un cubo más común:
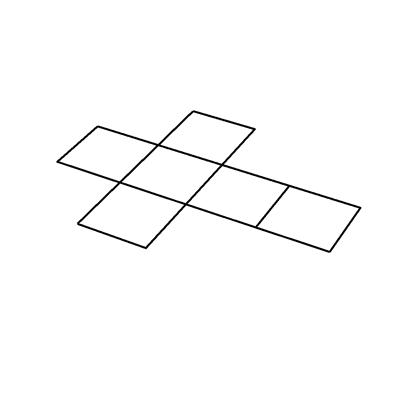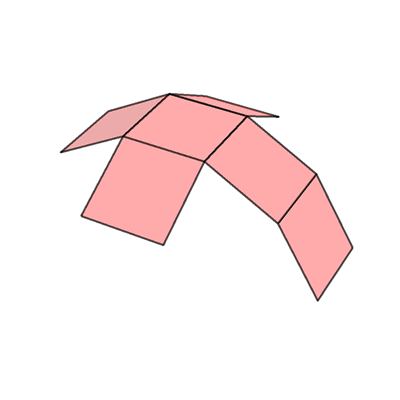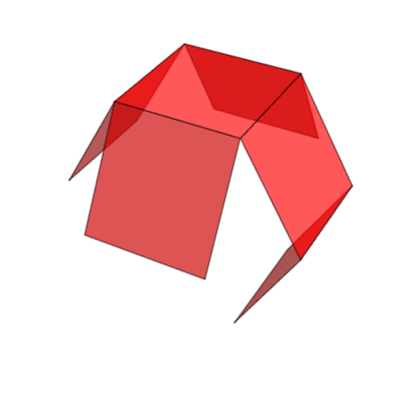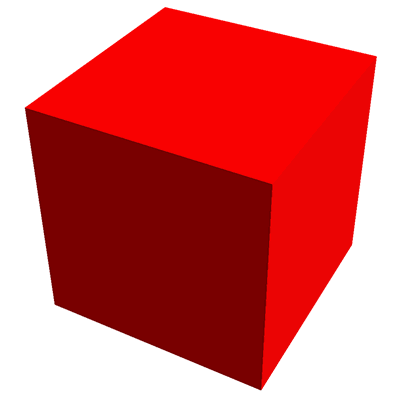
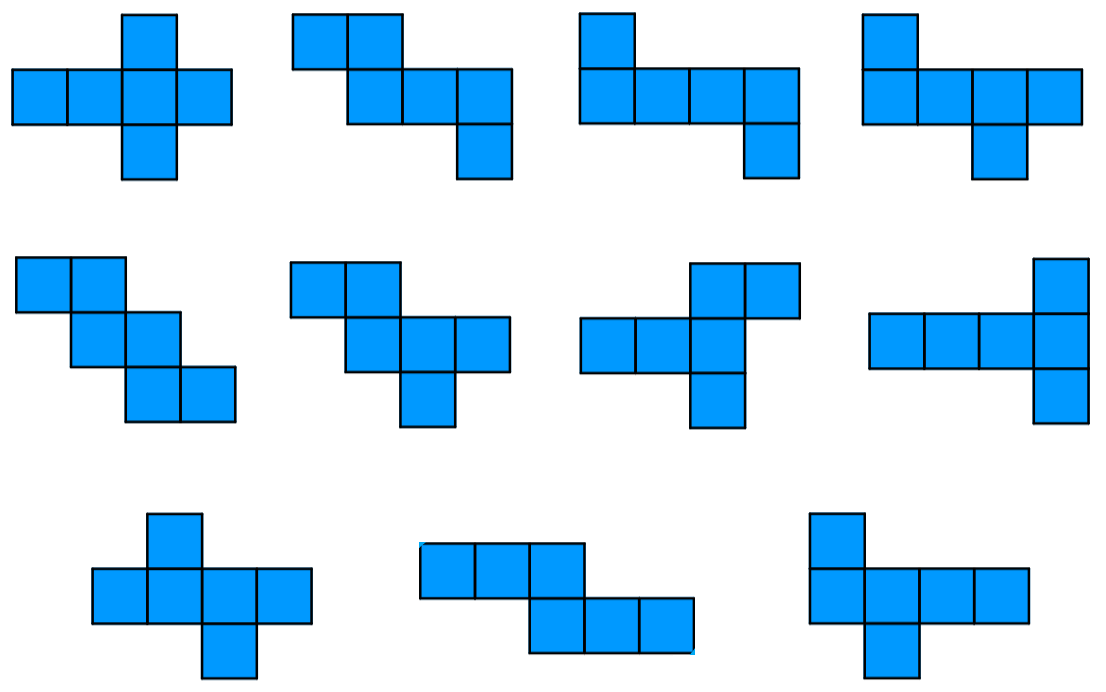
Adicionalmente, también existen otras formas de formar redes geométricas de un cubo. Las siguientes son todas las posibilidades. Observa que si es que doblamos cualquiera de estas redes, podemos formar un cubo.
Redes geométricas de un cono
Un cono es una figura tridimensional que tiene una base circular y una superficie lateral con una parte superior puntiaguda. Esto significa que la red geométrica debe incluir a la base circular y una superficie curva. En la siguiente animación, podemos observar cómo la red geométrica de un cono es formada.
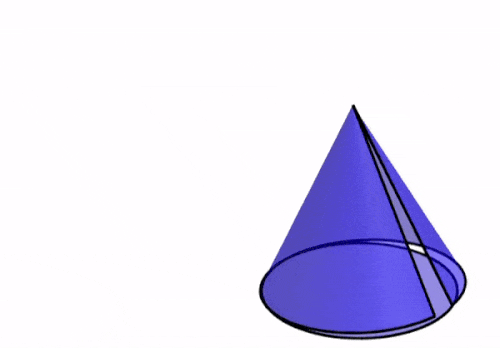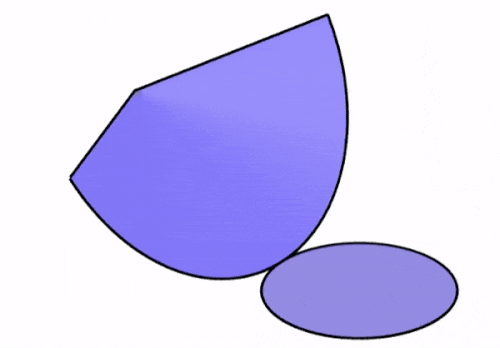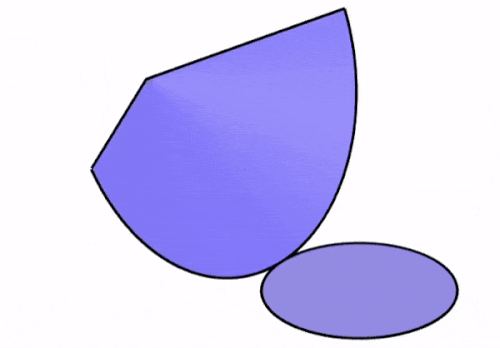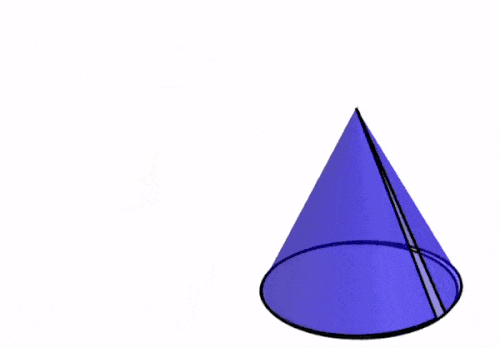
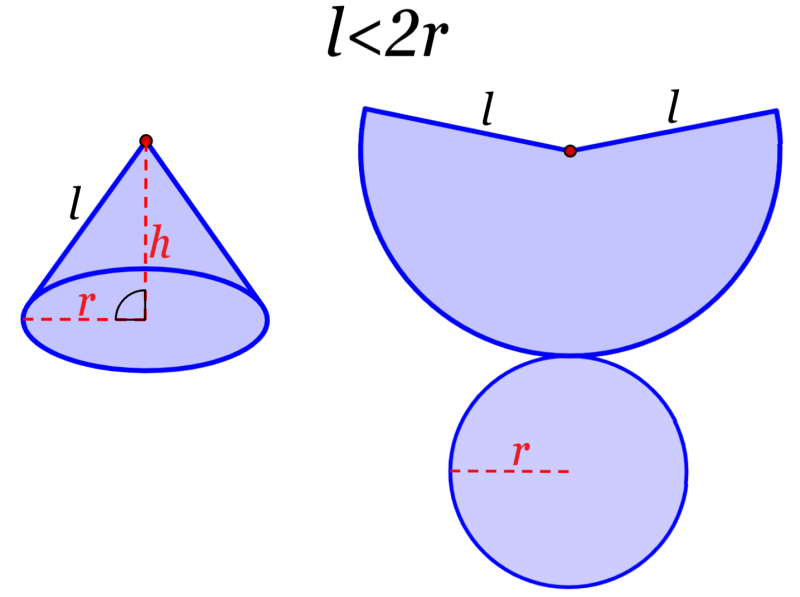
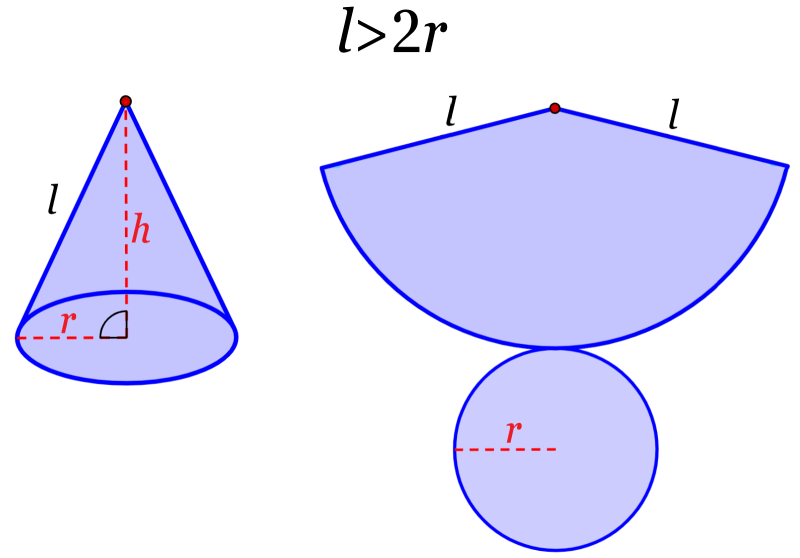
Dependiendo de la relación entre el radio y la altura del cono, podemos obtener tres variaciones de su red geométrica, las cuales son mostradas en el siguiente diagrama.
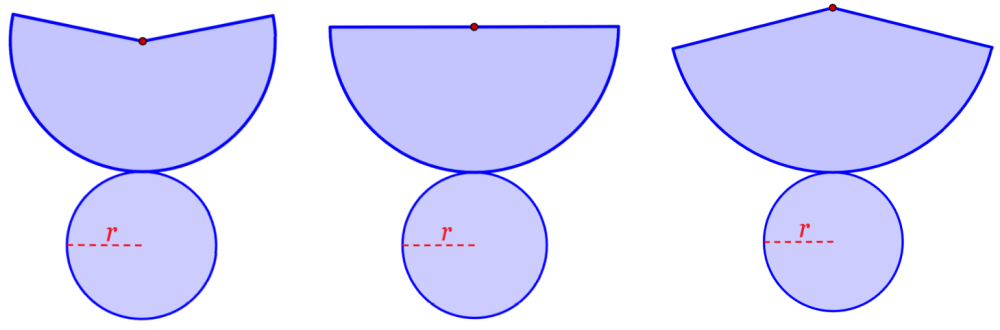
Para determinar cuál de las tres redes corresponde a un determinado cono, tenemos que comparar las longitudes del radio y del lado lateral del cono. Entonces, tenemos lo siguiente:
1. Si es que el lado lateral tiene una longitud igual a 2r (equivalente al diámetro), el cono formará la siguiente red geométrica:
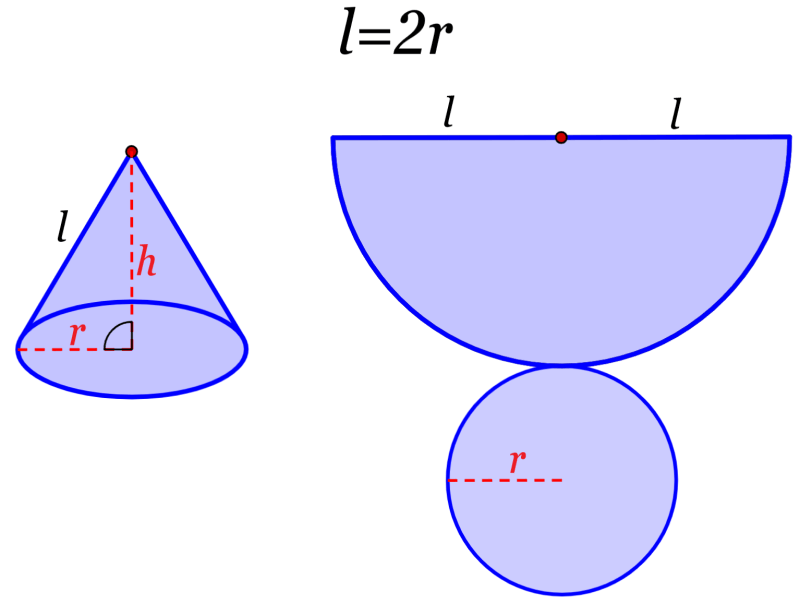
2. Si es que el lado lateral tiene una longitud menor a 2r, el cono formará la siguiente red geométrica:
3. Si es que el lado lateral tiene una longitud mayor a 2r, el cono formará la siguiente red geométrica:
Red geométrica de un cilindro
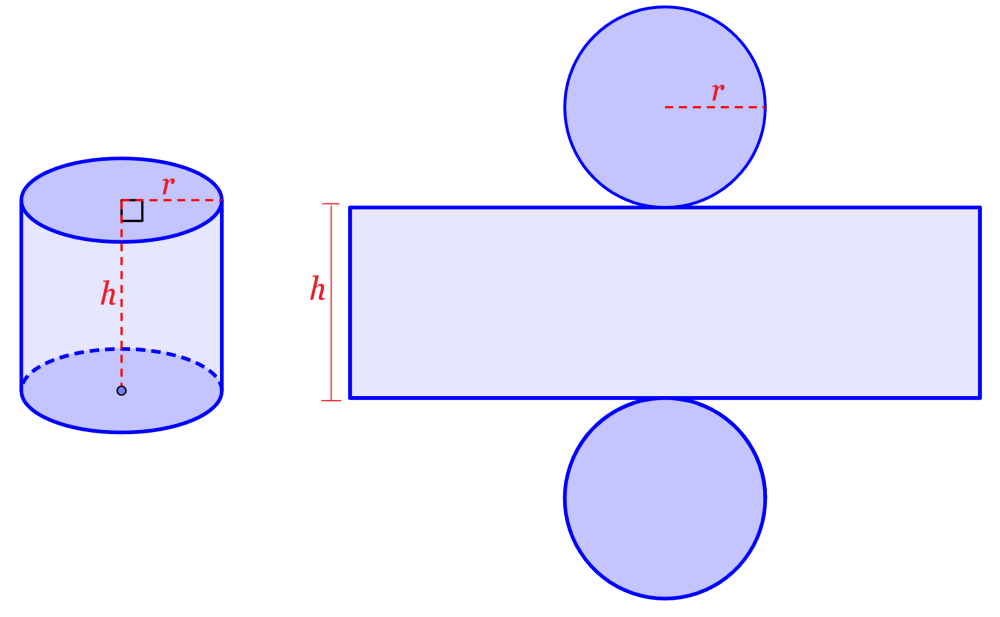
Un cilindro es una figura tridimensional compuesta de dos bases circulares y una superficie que conecta a las dos bases. La red geométrica de un cilindro contiene a las dos bases circulares y a un rectángulo, el cual forma la superficie curva al ser doblado.
En la siguiente animación, podemos observar cómo la red geométrica de un cilindro es formada.
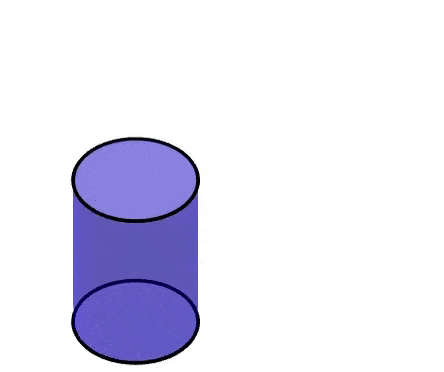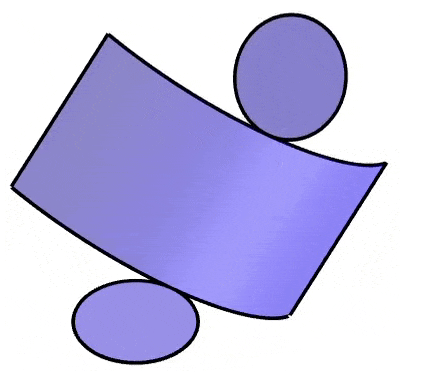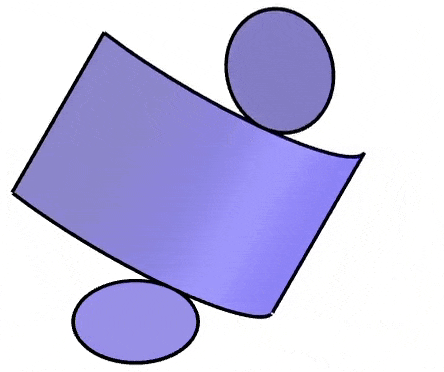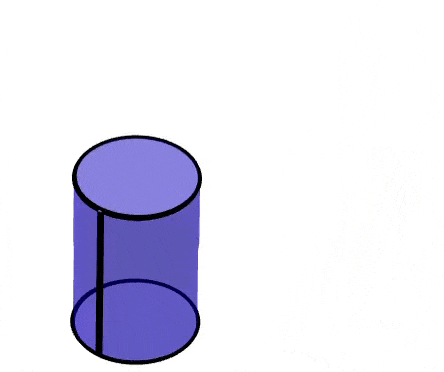
Podemos observar que las bases permanecen sin ningún cambio. El radio y por lo tanto el área de las bases circulares es la misma en el cilindro y en su red geométrica.
Sin embargo, la superficie curva del cilindro se extiende para formar un rectángulo. La altura del rectángulo es igual a la altura del cilindro.
La longitud del rectángulo corresponde a la circunferencia de las bases circulares. Entonces, la longitud del rectángulo es igual a 2πr, en donde r es el radio de las bases.
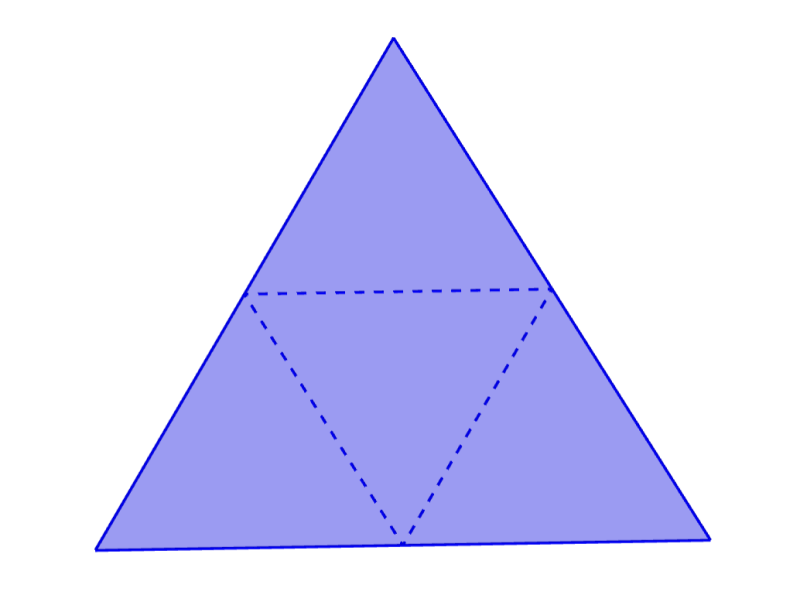
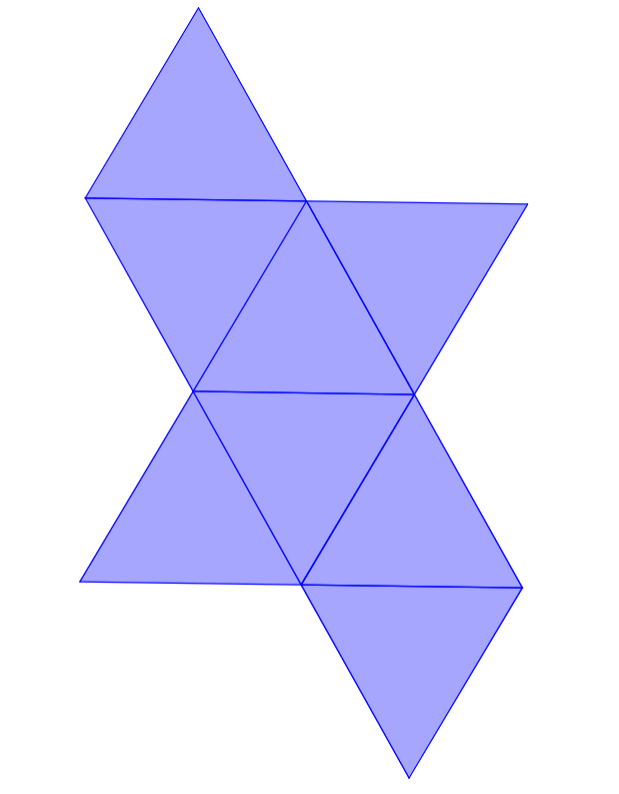
Red geométrica de un tetraedro
Los tetraedros son figuras tridimensionales formadas por cuatro caras triangulares. Una cara triangular es la base y las otras tres caras forman la superficie lateral que conectan en el vértice superior. Esto significa que la red geométrica debe incluir cuatro caras triangulares.
En la siguiente animación, podemos observar cómo se dobla la red geométrica de un tetraedro para formar al tetraedro tridimensional.
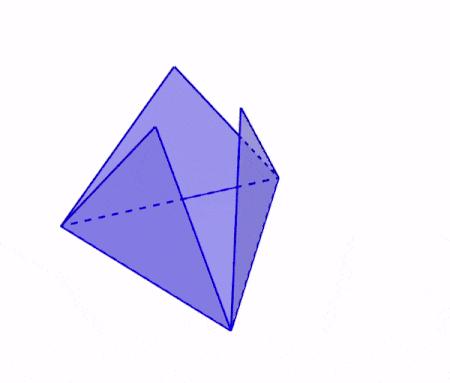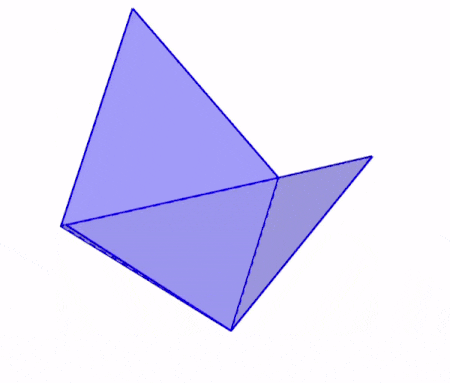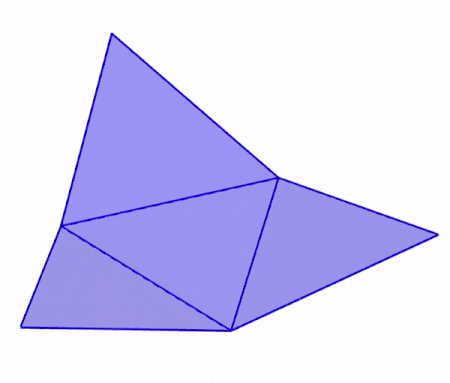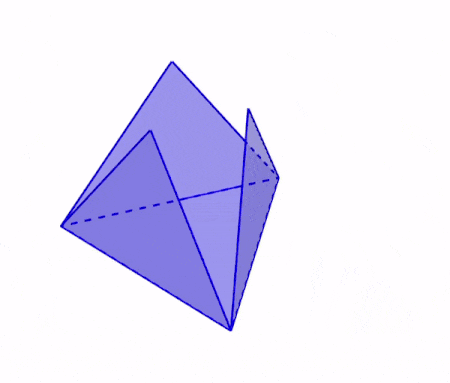
Podemos observar que la base del tetraedro permanece sin ningún cambio. Cada cara lateral se dobla en cada arista de la base hasta conectar en el vértice superior.
Cuando hablamos de tetraedros, normalmente nos referimos a un tetraedro regular, por lo que las cuatro caras serán triángulos equiláteros congruentes.
Red geométrica de un octaedro
Los octaedros son uno de los cinco sólidos Platónicos. Estas figuras tridimensionales tienen ocho caras triangulares congruentes. Es decir, las caras tienen la misma forma y las mismas dimensiones.
Esto significa que la red geométrica de un octaedro debe incluir ocho caras triangulares congruentes.
En la siguiente animación, podemos observar cómo se dobla la red geométrica de un octaedro para formar al octaedro tridimensional.
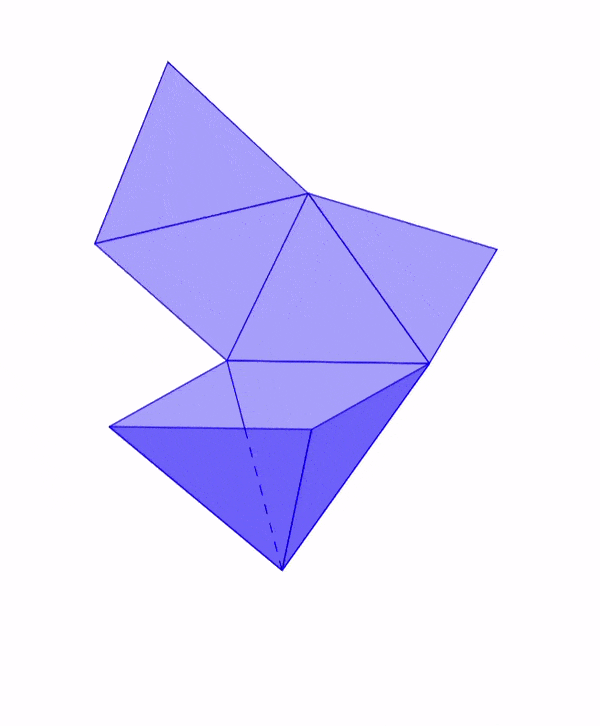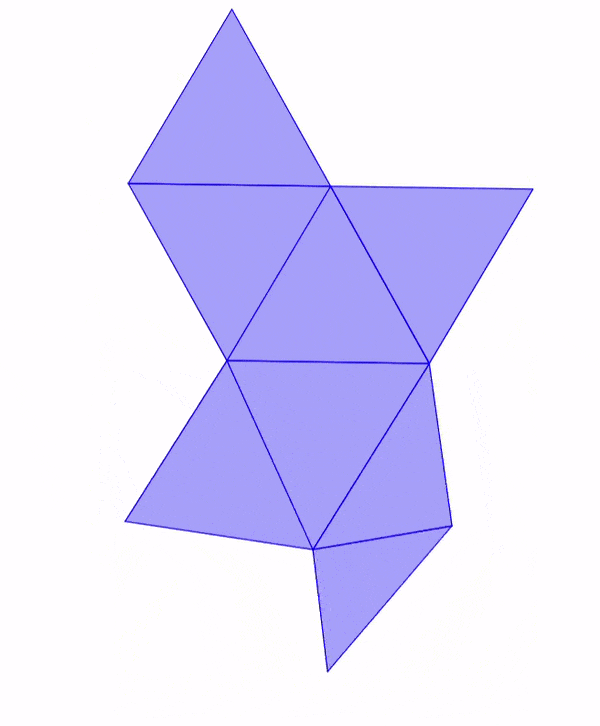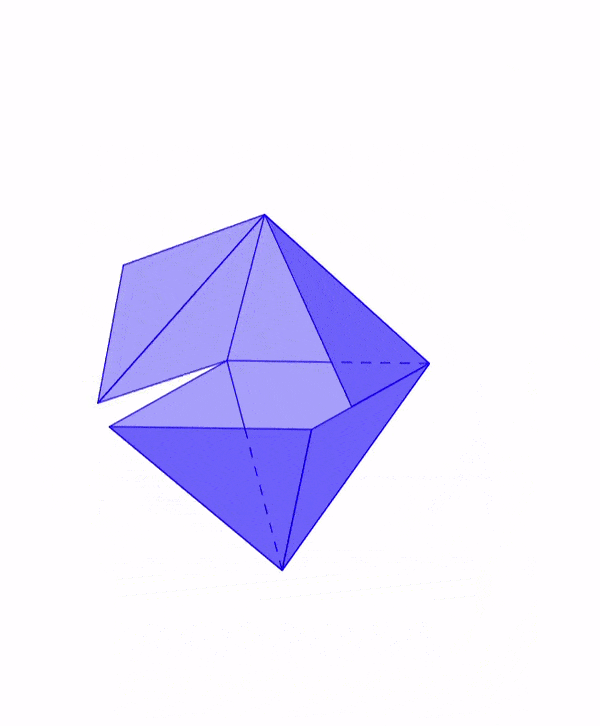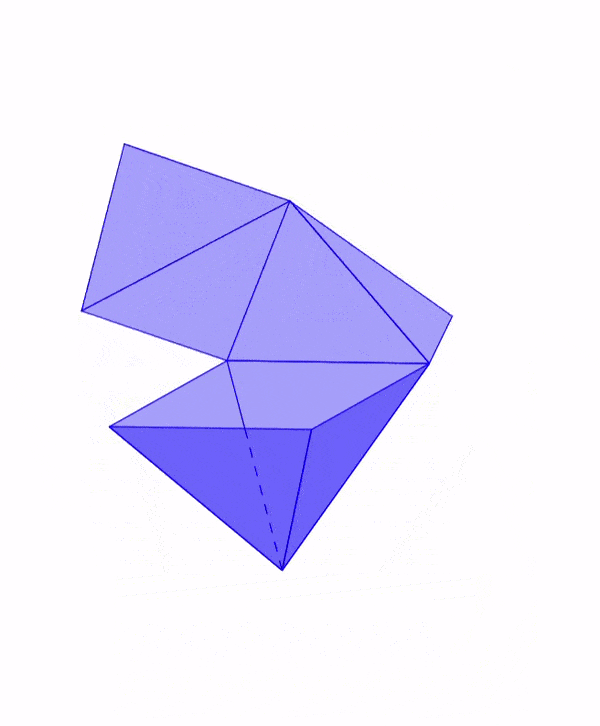
Dado que el octaedro consiste de dos pirámides cuadradas unidas en su base, podemos doblar cada una de estas pirámides separadamente. En el diagrama, vemos que las caras laterales de cada pirámide son dobladas alrededor de las caras que actúan como bases temporales.
Cuando hablamos de octaedros, normalmente nos referimos a un octaedro regular, por lo que las ocho caras serán triángulos equiláteros congruentes.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
