El área de figuras geométricas representa a la región cubierta por la figura en el espacio. El área es una de las medidas más importantes de las figuras geométricas. El área es una medida bidimensional, por lo que tiene unidades cuadradas, como m², cm², etc. Podemos calcular el área tanto de figuras bidimensionales, como de figuras tridimensionales. La fórmula del área depende de la forma de la figura y de sus dimensiones.
A continuación, conoceremos las fórmulas de las áreas de las figuras geométricas más importantes. Luego, aplicaremos estas fórmulas para resolver algunos ejercicios.
Definición del área
El área de una figura geométrica es definida como la región ocupada por una figura en el espacio. El área es una de las medidas más importantes de las figuras geométricas. Dado que el área es una medida bidimensional, usamos unidades cuadradas para medirla. Por ejemplo, podemos usar m², cm², etc.
El área puede ser calculada de una figura 2D, así como también de una figura 3D. En el caso de la figura 3D, el área es denominada área superficial y es el área de todas las caras de la figura. Para que dos figuras tengan la misma área, su forma y sus dimensiones deben ser las mismas.
Fórmulas del área de figuras 2D
Las fórmulas del área dependen de la forma de la figura 2D. Las figuras 2D más importantes son el cuadrado, el triángulo, el rectángulo, el círculo, el paralelogramo, el trapecio y la elipse.
Área de un rectángulo
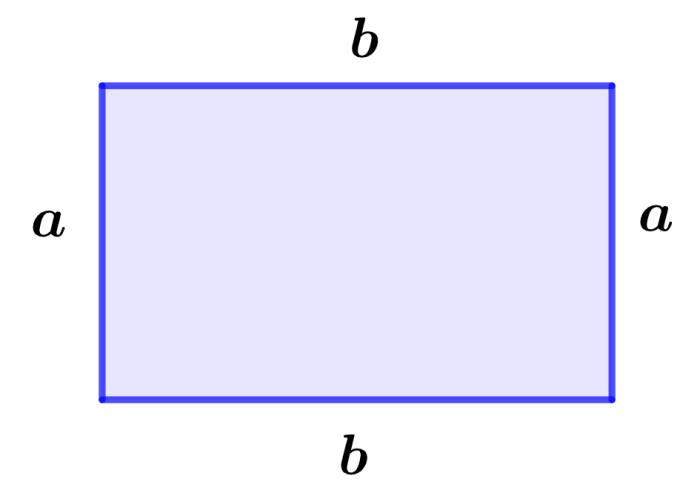
Un rectángulo es una figura que tiene cuatro ángulos internos de 90°. Los lados opuestos de un rectángulo tienen la misma longitud.
Área de rectángulo = a×b
en donde, a representa al ancho del rectángulo y b representa a su longitud.
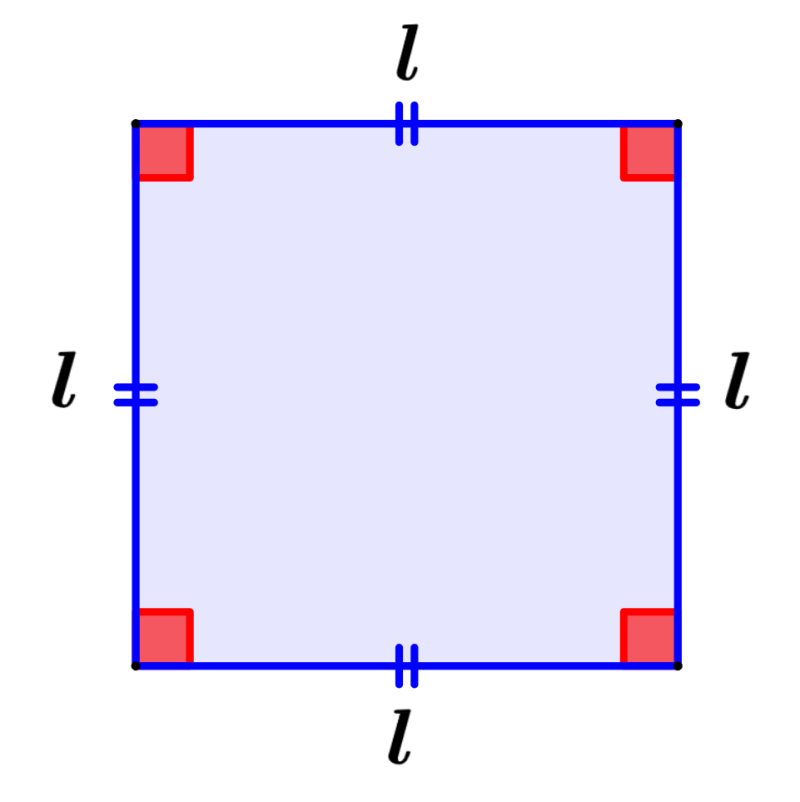
Área de un cuadrado
Un cuadrado es definido como un tipo especial de rectángulo que tiene todos sus lados con la misma longitud.
Área de un cuadrado = l²
en donde, l representa a la longitud de uno de los lados del cuadrado.
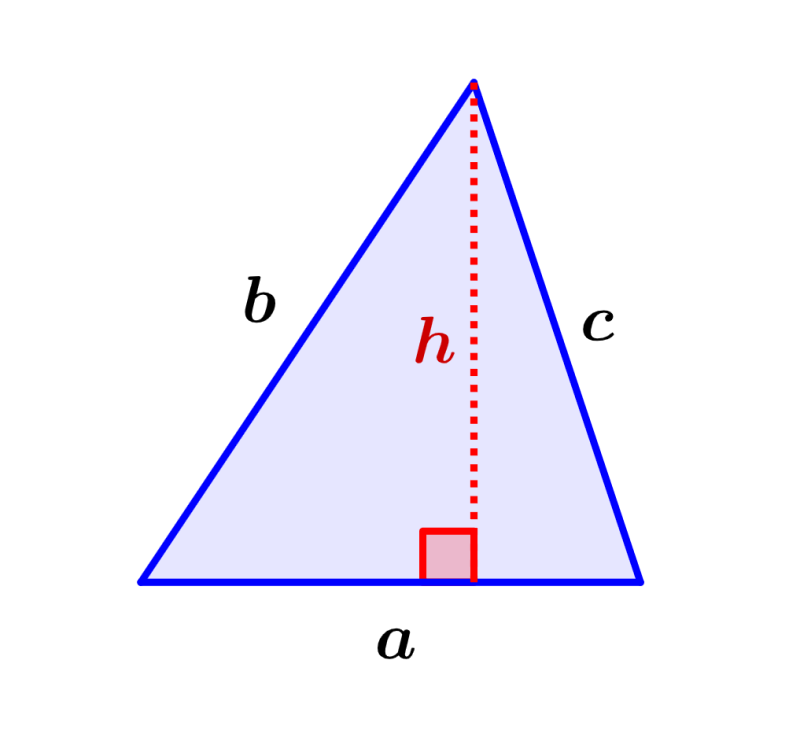
Área de un triángulo
Un triángulo es definido como un polígono de tres lados. Existen tres tipos principales de triángulos: equilátero, isósceles y escaleno. Sin embargo, la fórmula del área aplica para cualquier tipo de triángulo.
Área de un triángulo = ½ha
en donde, h representa a la altura y a representa a la base del triángulo.
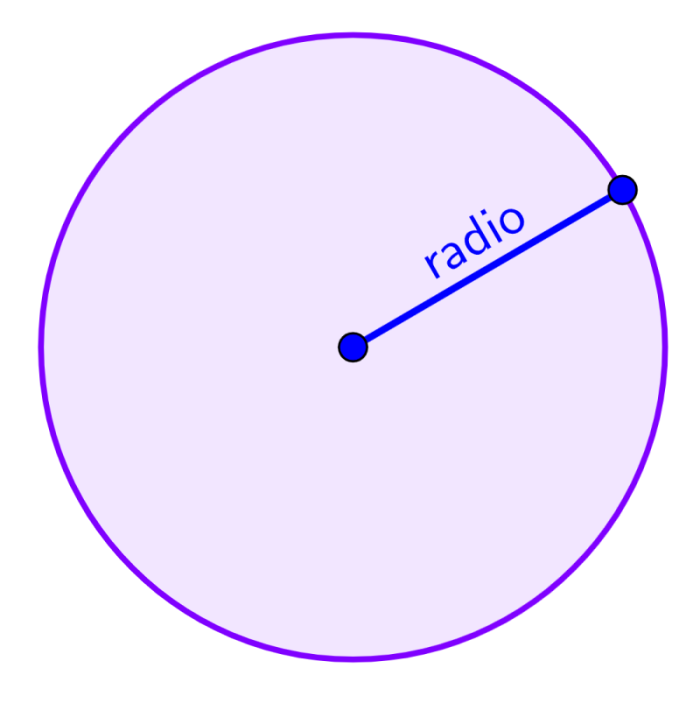
Área de un círculo
El círculo es definido como el conjunto de puntos que se ubican a la misma distancia desde un punto central. Esa distancia es denominada el radio y es usado para calcular el área del círculo.
Área del círculo = πr²
en donde, r representa al radio y π es una constante numérica con un valor aproximado de 3.1415…
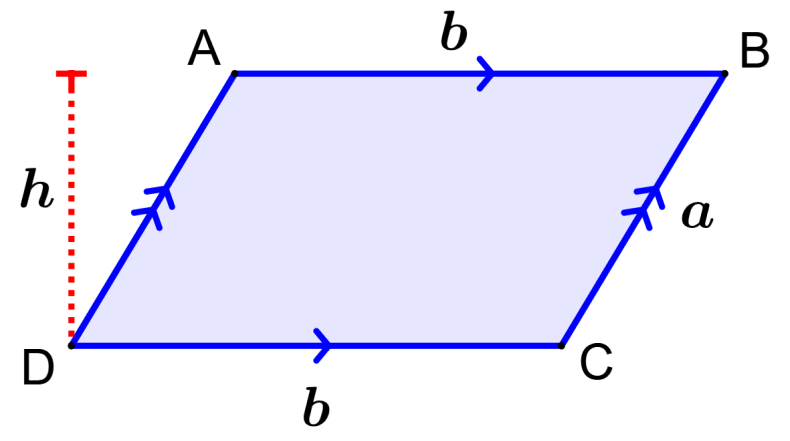
Área de un paralelogramo
El paralelogramo es una figura en la que sus lados opuestos son paralelos el uno con el otro. La altura del paralelogramo es usada para calcular su área.
Área de un paralelogramo: bh
en donde, b es la longitud de la base y h es la longitud de la altura.
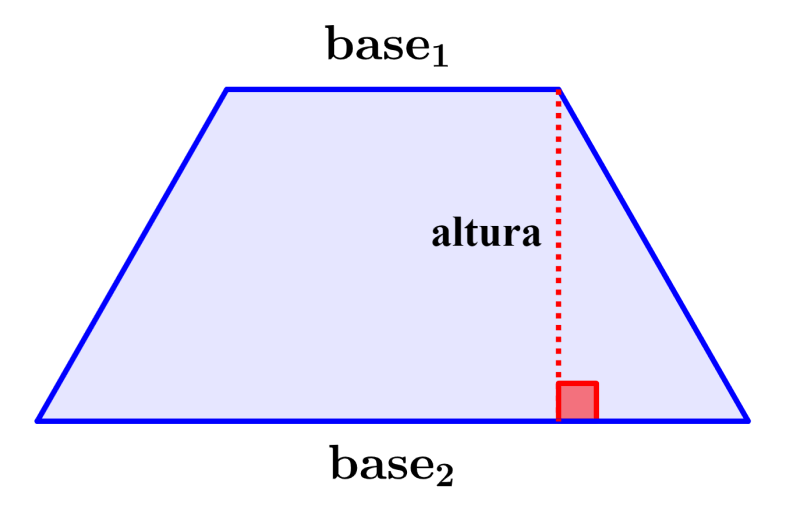
Área de un trapecio
El trapecio es una figura de cuatro lados en la que al menos dos de sus lados son paralelos. Los lados paralelos son llamados las bases del trapecio.
Área de un trapecio: $latex \frac{a+b}{2}h$
en donde, a y b son las longitudes de ambas bases y h es la altura del trapecio.
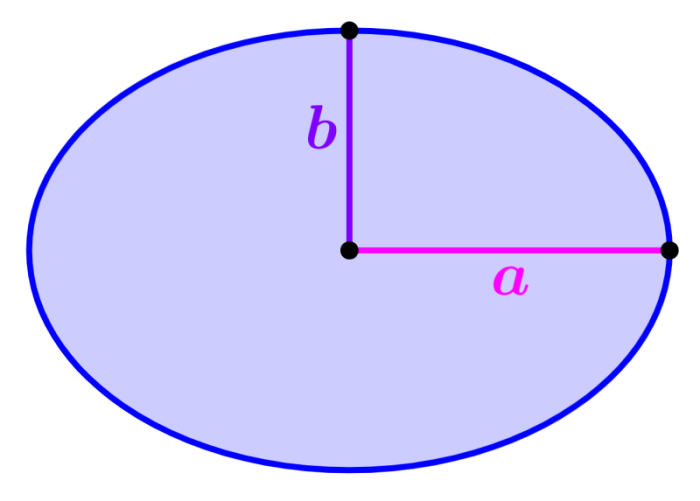
Área de una elipse
Una elipse es una figura que tiene una forma circular elongada.
Área de una elipse: πab
en donde, a es la mitad de la longitud del eje mayor y b es la mitad de la longitud del eje menor.
| Figura | Área | Términos |
| Círculo | A = πr² | r=radio |
| Triángulo | A = ½ bh | b=base, h=altura |
| Cuadrado | A = l² | l=longitud de un lado |
| Rectángulo | A = ab | a=ancho, b=base |
| Paralelogramo | A = bh | b=base, h=altura |
| Trapecio | A = $latex \frac{a+b}{2}h$ | a y b=bases, h=altura |
| Elipse | A = πab | a=½eje mayor, b=½eje menor |
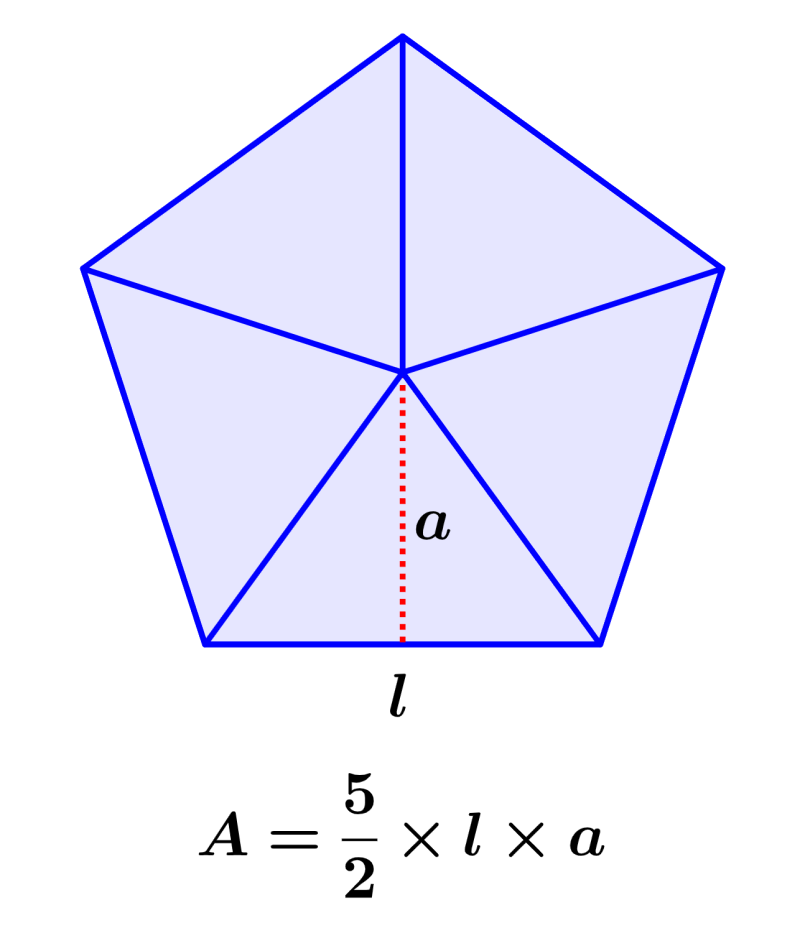
| Polígono regular | A = ½ nla | n=n° de lados, l=longitud de un lado, a=apotema |
Fórmulas del área de figuras 3D
En el caso de figuras 3D, su área es denominada área superficial. Las figuras 3D más importantes son el cubo, el prisma rectangular, el cilindro, el cono, la esfera, la pirámide triangular y la pirámide rectangular.
Área de un cubo
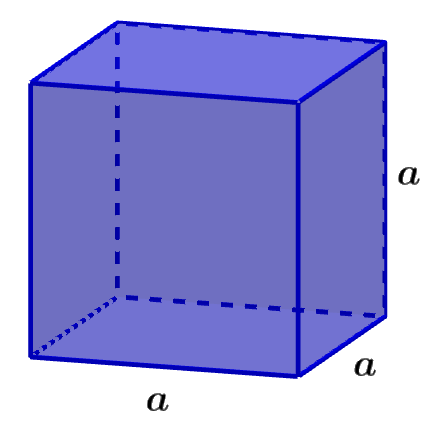
Un cubo es una figura tridimensional que tiene todos sus lados de igual longitud. Un cubo tiene un total de seis caras cuadradas y su área es igual a la suma de todas las caras.
Área de un cubo = 6a²
en donde, a es la longitud de uno de los lados del cubo.
Área de un prisma rectangular
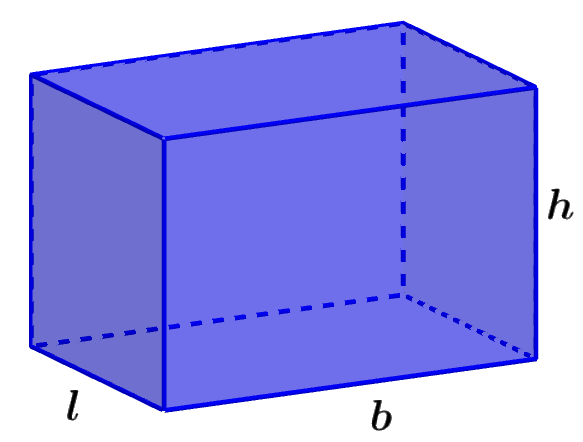
El prisma rectangular es una figura 3D con seis caras rectangulares. Las caras opuestas de un prisma rectangular son iguales.
Área de un prisma rectangular = 2(lb+lh+hb)
en donde, l es la longitud del ancho, b es la longitud de la base y h es la longitud de la altura.
Área de un cilindro
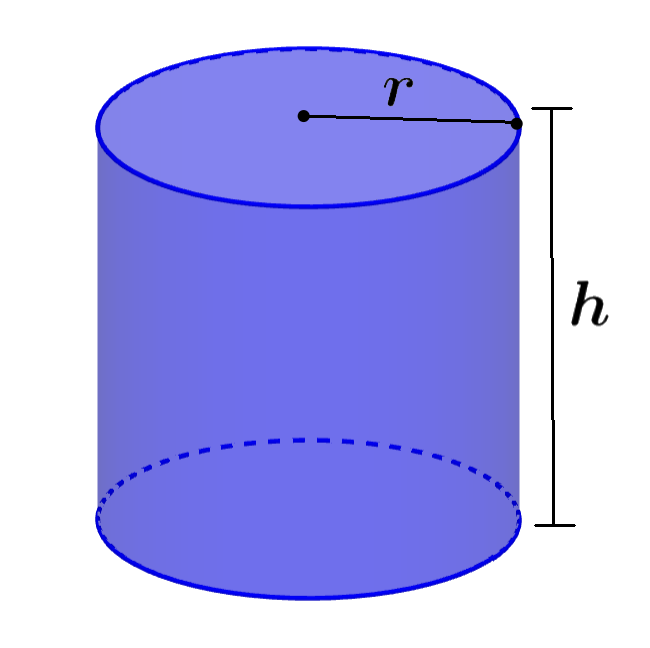
Un cilindro es una figura tridimensional que tiene dos bases circulares, las cuales son unidas y están cubiertas por una superficie.
Área de un cilindro = 2πr(r+h)
en donde, r es el radio de una de las caras del cilindro, h es la altura y π es una constante matemática con un valor aproximado a 3.1415…
Área de una pirámide triangular
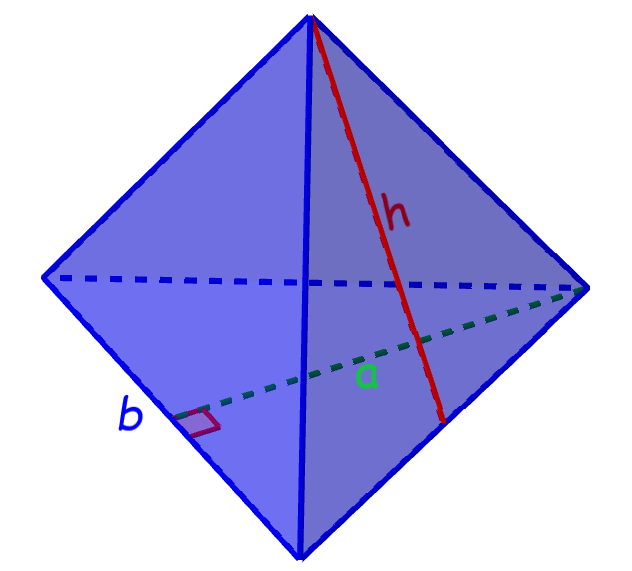
Una pirámide triangular es una figura tridimensional que tiene cuatro caras triangulares, por lo que también es denominada tetraedro.
Área de una pirámide triangular = $latex \frac{1}{2}ba+\frac{3}{2}bh$
en donde, b es la longitud de uno de los lados de la base, a es la altura del triángulo en la base y h es la altura de uno de los triángulos laterales.
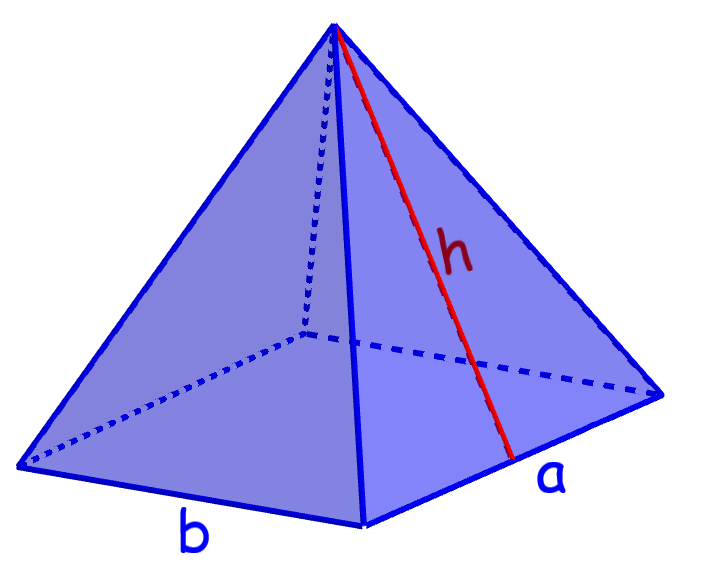
Área de una pirámide rectangular
Una pirámide rectangular es una figura que tiene una base rectangular y cuatro caras triangulares laterales.
Área de una pirámide rectangular = ba+bh+ah
en donde, a y b son las longitudes de la base rectangular y h es la altura de una cara lateral triangular.
Área de una esfera
Una esfera es una figura tridimensional que es perfectamente redonda. Cada punto en la esfera está ubicado a una misma distancia desde el centro.
Área de una esfera= 4πr²
en donde, r es el radio de la esfera y π es una constante numérica que tiene un valor de 3.1415…
| Figura | Área | Términos |
| Cubo | A = 6a² | a=longitud de un lado |
| Prisma rectangular | A = 2(lb+lh+hb) | l=ancho, b=base, h=altura |
| Cilindro | A = 2πr(r+h) | r=radio de bases, h=altura |
| Pirámide triangular | A = $latex \frac{1}{2}ba+\frac{3}{2}bh$ | b=lados de base, a=altura de base, h=altura de caras laterales |
| Pirámide rectangular | A = ba+bh+ah | a y b=lados de base, h=altura de caras laterales |
| Cono | A = πr(r+l) | r=radio de base, l=altura inclinada |
| Esfera | A = 4πr² | r=radio |
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
