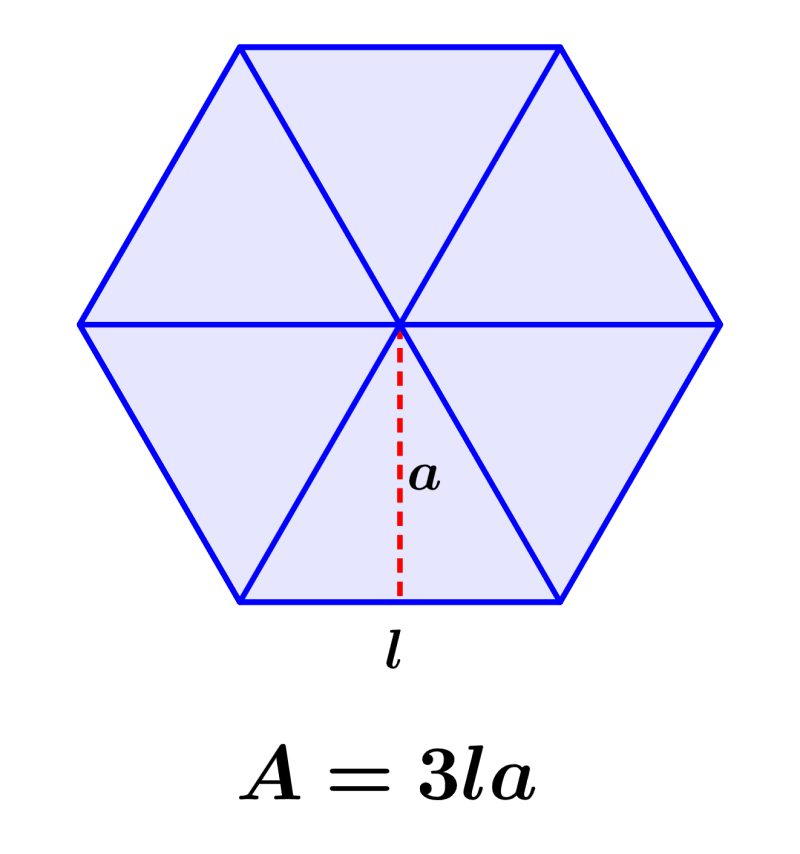
El área de los polígonos regulares es usada para medir la región cubierta por el polígono en el espacio bidimensional. Dado que es una región bidimensional, usamos unidades cuadradas para medir el área. El área de un polígono regular puede ser calculada usando la longitud de su apotema y la longitud de uno de sus lados. Sin embargo, también es posible calcular el área de polígonos regulares usando simplemente la longitud de uno de sus lados.
A continuación, conoceremos las fórmulas que podemos usar para calcular el área de estos polígonos. Luego, aplicaremos estas fórmulas para resolver algunos ejercicios.
Calcular el área de polígonos regulares usando la apotema y los lados
El área de cualquier polígono regular puede ser calculada usando la longitud de su apotema y la longitud de uno de sus lados. La fórmula del área en estos casos es:
$latex A=\frac{1}{2}nal$
en donde, a es la longitud de la apotema y l es la longitud de uno de los lados y n es el número de lados del polígono.
Esta fórmula es derivada del hecho que podemos dividir en triángulos congruentes a cualquier polígono regular. Por ejemplo, consideremos al siguiente hexágono regular:
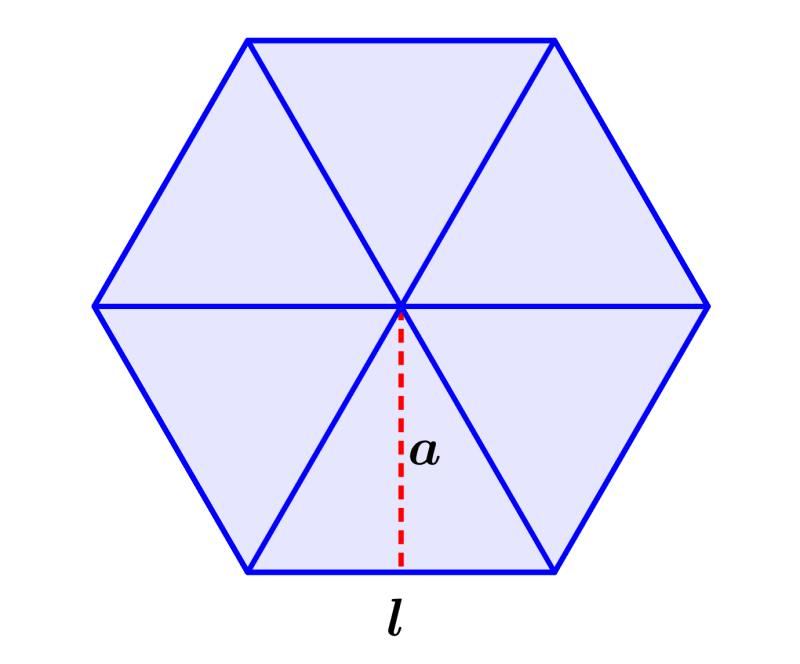
Podemos dividir a este hexágono en seis triángulos congruentes. Sabemos que el área de un triángulo es igual a un medio de su base multiplicada por su altura. En este caso, la altura del triángulo es la apotema y la base es igual a uno de los lados del hexágono. Entonces, el área de cada triángulo es:
$latex A_{t}=\frac{1}{2}al$
Ahora, vemos que tenemos seis de estos triángulos (lo cual es igual al número de lados del hexágono). Entonces, el área del hexágono es:
$latex A=\frac{1}{2}(6)al$
$latex A=3al$
Calcular el área de polígonos regulares usando solo los lados
El área de polígonos regulares también puede ser calculada usando solamente la longitud de uno de sus lados. Para lograr esto, podemos usar la fórmula del área que vimos anteriormente. Sin embargo, necesitamos encontrar una expresión para la apotema en términos de sus lados.
Una expresión puede ser encontrada usando trigonometría. Podemos usar a la función tangente para encontrar a la apotema. Entonces, la fórmula resultante es la siguiente:
$latex A=\frac{{{a}^2}n}{4\tan(\frac{180}{n})}$
en donde, a es la longitud de uno de los lados del polígono y n es el número de lados.
Ejercicios de área de polígonos regulares resueltos
Las áreas de los siguientes polígonos regulares son encontradas usando las fórmulas vistas arriba. Cada ejercicio tiene su respectiva solución, en donde puedes observar el proceso usado.
EJERCICIO 1
Si es que un pentágono tiene lados de longitud de 8 m y una apotema de 5.5 m, ¿cuál es su área?
Solución
Un pentágono es un polígono regular de cinco lados. Usamos la fórmula del área para polígonos regulares con las longitudes $latex l=8$ y $latex a=5.5$. Entonces, tenemos:
$latex A=\frac{1}{2}nla$
$latex A=\frac{1}{2}(5)(8)(5.5)$
$latex A=110$
Entonces, el área del pentágono es 110 m².
EJERCICIO 2
¿Cuál es el área de un heptágono que tiene lados de longitud de 8 m y una apotema de 8.3 m?
Solución
El heptágono es un polígono regular de siete lados, por lo que tenemos $latex n=7$. Además, tenemos las longitudes $latex l=8$ y $latex a=8.3$. Entonces, usando la fórmula del área con estos valores, tenemos:
$latex A=\frac{1}{2}nla$
$latex A=\frac{1}{2}(7)(8)(8.3)$
$latex A=232.4$
Entonces, el área del heptágono es 232.4 m².
EJERCICIO 3
Determina el área de un hexágono que tiene lados de 10 m.
Solución
El hexágono es un polígono regular de seis lados, por lo que tenemos $latex n=6$. En este caso, solo tenemos la longitud $latex l=10$. Entonces, usando la segundo fórmula del área:
$latex A=\frac{{{l}^2}n}{4\tan(\frac{180}{n})}$
$latex A=\frac{{{(10)}^2}(6)}{4\tan(\frac{180}{6})}$
$latex A=\frac{600}{4\tan(30)}$
$latex A=\frac{600}{2.31}$
$latex A=259.7$
Entonces, el área del hexágono es 259.7 m².
EJERCICIO 4
Si es que un octágono tiene lados de longitud de 5 m, ¿cuál es su área?
Solución
El octágono es un polígono regular de ocho lados, por lo que tenemos $latex n=8$. Similar al ejercicio anterior, solo tenemos la longitud $latex l=5$. Entonces, usamos estos valores en la segunda fórmula del área:
$latex A=\frac{{{l}^2}n}{4\tan(\frac{180}{n})}$
$latex A=\frac{{{(5)}^2}(8)}{4\tan(\frac{180}{8})}$
$latex A=\frac{200}{4\tan(22.5)}$
$latex A=\frac{200}{1.66}$
$latex A=120.5$
Entonces, el área del octágono es 120.5 m².
Ejercicios de volumen de figuras geométricas para resolver
Aplica las fórmulas del volumen de figuras tridimensionales para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
