El área y el perímetro son dos de las medidas más importantes de figuras geométricas. El perímetro representa a la suma total de las longitudes de los lados de una figura geométrica. Por otra parte, el área representa a la región cubierta por la figura. El perímetro es una medida unidimensional y el área es una medida bidimensional, por lo que el perímetro puede ser medido en m, cm, etc., mientras que el área puede ser medida en m², cm², etc.
A continuación, conoceremos las fórmulas del área y del perímetro de figuras geométricas importantes. Luego, aplicaremos estas fórmulas al resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Conocer las fórmulas del área y perímetro de figuras geométricas.
GEOMETRÍA
Relevante para…
Conocer las fórmulas del área y perímetro de figuras geométricas.
Definición del área
El área de una figura geométrica es definida como la región cubierta por la figura. El área es una medida bidimensional, por lo que usamos unidades cuadradas como m² o cm² para medirla. La fórmula del área depende de la forma de la figura geométrica. Dependiendo de la forma de una figura, necesitaremos diferentes dimensiones para encontrar su área.
Para que dos figuras geométricas tengan la misma área, deben tener la misma forma y las mismas dimensiones. Por ejemplo, podemos imaginar que tenemos a un rectángulo que tiene un ancho de longitud A y una base de longitud B.
Ahora, imaginemos que tenemos a un segundo rectángulo con ancho de longitud C y base de longitud D. Para que el área de estos dos rectángulos sea la misma, debemos tener A=C y B=D.
Definición del perímetro
El perímetro de una figura geométrica es la distancia total alrededor de sus límites. El perímetro es calculado al sumar las longitudes de todos los lados de la figura. Dado que el perímetro es una longitud, usamos unidades unidimensionales como metros o centímetro para medirlo.
Debido a la naturaleza del perímetro, es posible que dos figuras que tienen diferentes formas puedan tener el mismo perímetro dependiendo de las dimensiones de sus lados. Por ejemplo, es posible formar a un círculo usando una cuerda y luego, usar la misma cuerda para formar a un cuadrado.
La fórmula del perímetro es diferente para diferentes figuras geométricas dependiendo en el número de lados y la forma de la figura.
Fórmulas del área y perímetro de varias figuras geométricas
Hay una gran variedad de figuras geométricas, por lo que necesitamos varias fórmulas para calcular su área y perímetro. Sin embargo, podemos familiarizarnos con las fórmulas de las figuras geométricas más comunes, las cuales son el cuadrado, el triángulo, el rectángulo y el círculo.
Fórmulas para un rectángulo
Un rectángulo es definido como una figura 2D de cuatro lados con ángulos rectos. Todos los ángulos internos en un rectángulo miden 90° y sus lados opuestos son paralelos e iguales.
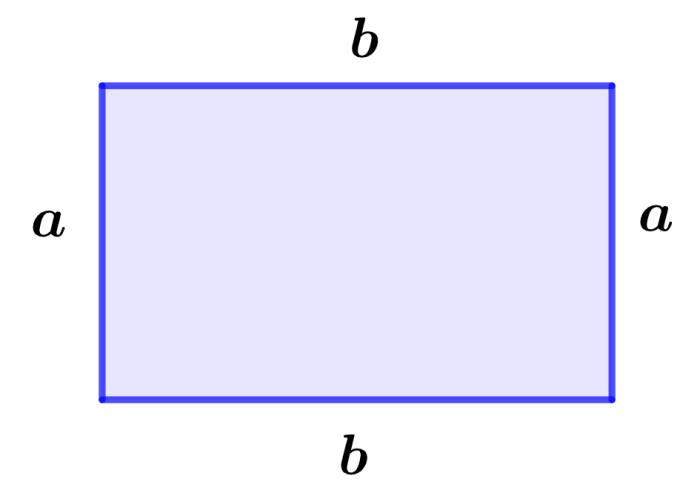
Fórmula del Área = a×b
Fórmula del Perímetro = 2(a+b)
en donde, a representa al ancho del rectángulo y b representa a su base.
Fórmulas para un cuadrado
Un cuadrado es definido como una figura 2D que tiene cuatro lados de igual longitud. Un cuadrado es un tipo especial de rectángulo, ya que todos sus ángulos internos miden 90°.
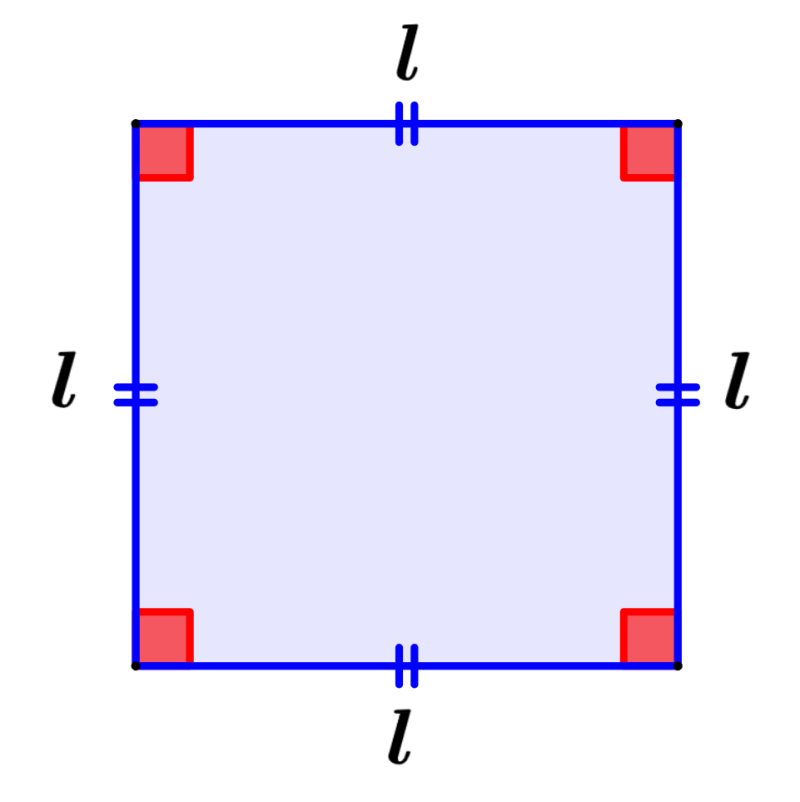
Fórmula del Área = l²
Fórmula del Perímetro = 4l
en donde, l representa a la longitud de uno de los lados del cuadrado.
Fórmulas para un triángulo
El triángulo es una figura 2D con tres lados. Existen tres tipos de triángulos dependiendo en las longitudes de sus lados: el triángulo equilátero, el triángulo isósceles y el triángulo escaleno. Las fórmulas para calcular el área y el perímetro son las mismas para cualquier tipo de triángulos.
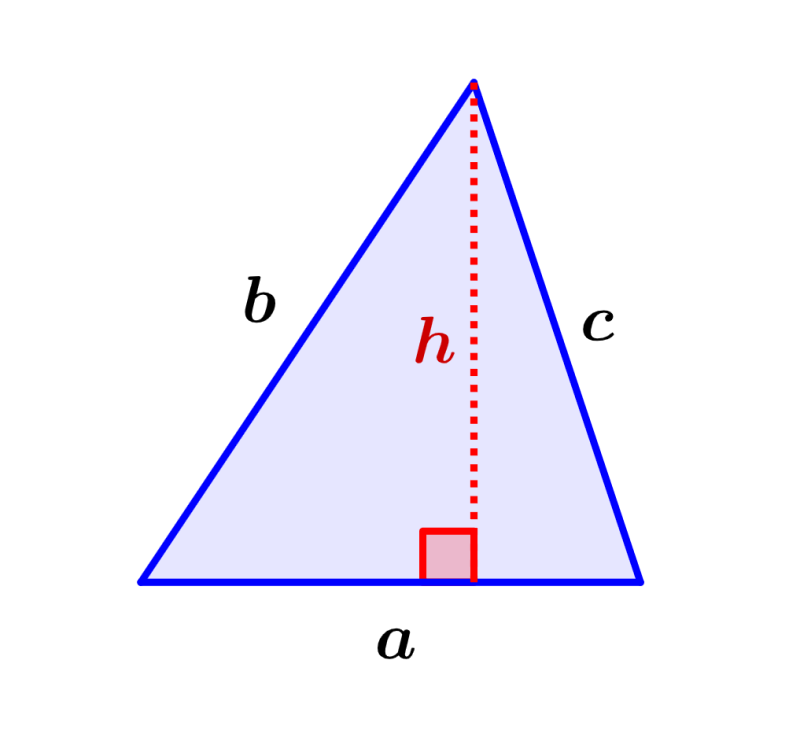
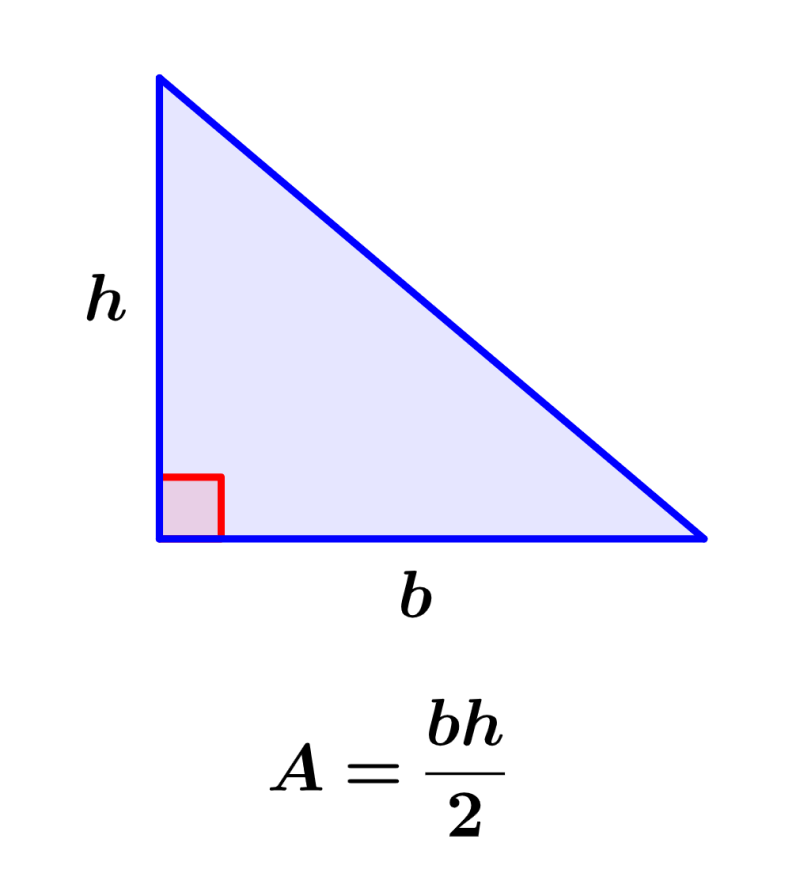
Fórmula del Área = ½ha
Fórmula del Perímetro = a+b+c
en donde, a, b, c representan a las longitudes de los lados del triángulo, h representa la altura y a representa la base del triángulo.
Fórmulas para un círculo
El círculo es una figura 2D que se caracteriza por tener una forma completamente redonda. El radio del círculo es usado para calcular su área y su perímetro.
Fórmula del Área = πr²
Fórmula del Perímetro = 2πr
en donde, r representa al radio del círculo y π es una constante matemática que tiene un valor de 3.1415…
Tabla de fórmulas de área y perímetro
| Figura | Área | Perímetro |
| Círculo | A = πr² | P = 2πr |
| Triángulo | A = ½ bh | P = a+b+c |
| Cuadrado | A = l² | P = 4l |
| Rectángulo | A = ab | P = 2(a+b) |
| Paralelogramo | A = bh | P = 2(a+b) |
| Polígono regular | A = ½ nla | P = nl |
Círculo: r representa al radio y π es la contante matemática con un valor de 3.1415…
Triángulo: b representa a la base, h representa a la altura y a, b, c son las longitudes de los lados.
Cuadrado: l representa a la longitud de uno de los lados.
Rectángulo: a define a la longitud del ancho y b define a la longitud de la base.
Paralelogramo: b representa a la longitud de la base y h representa a la longitud de la altura.
Polígono regular: n define al número de lados del polígono regular, l representa a la longitud de uno de los lados y a representa a la longitud de la apotema. Recordemos que la apotema es la distancia perpendicular desde uno de los lados del polígono hasta el centro.
Ejercicios de área y perímetro de figuras geométricas resueltos
Las fórmulas del área y del perímetro de diferentes figuras geométricas son aplicadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde puedes mirar el proceso usado.
EJERCICIO 1
¿Cuál es el área de un triángulo que tiene una base de 9 m y una altura de 8 m?
Solución
Sabemos que el área de cualquier triángulo puede ser calculada al multiplicar a su base y a su altura y dividir por dos. Entonces, tenemos:
$latex A=\frac{1}{2}bh$
$latex A=\frac{1}{2}(9)(8)$
$latex A=36$
Entonces, el área del triángulo es 36 m².
EJERCICIO 2
¿Cuál es el área y el perímetro de un cuadrado que tiene lados de longitud de 11 m?
Solución
Podemos encontrar el área al elevar al cuadrado a la longitud de uno de los lados. El perímetro es encontrado al multiplicar por cuatro a la longitud de uno de sus lados. Entonces, tenemos:
$latex A={{l}^2}$
$latex A={{11}^2}$
$latex A=121$
$latex p=4l$
$latex p=4(11)$
$latex p=44$
Entonces, el área del cuadrado es 121 m² y el perímetro es 44 m.
EJERCICIO 3
Un rectángulo tiene lados de longitud 12 m y 15 m. ¿Cuál es su perímetro?
Solución
Encontramos el perímetro del rectángulo al sumar las longitudes de los lados y multiplicar por dos:
$latex p=2(a+b)$
$latex p=2(12+15)$
$latex p=2(27)$
$latex p=54$
Entonces, el perímetro del rectángulo es 54 m.
EJERCICIO 4
¿Cuál es la longitud de los lados de un cuadrado que tiene un perímetro de 60 m?
Solución
Tenemos la medida del perímetro y queremos encontrar la longitud de uno de los lados del cuadrado. Simplemente usamos la fórmula del perímetro y resolvemos para uno de los lados:
$latex p=4l$
$latex 60=4l$
$latex l=15$
Entonces, la longitud de un lado del cuadrado es 15 m.
EJERCICIO 5
¿Cuál es el área y el perímetro de un círculo que tiene un radio de 8 m?
Solución
Tanto el área como el perímetro del círculo son calculados usando la longitud del radio:
$latex A=\pi{{r}^2}$
$latex A=\pi{{(8)}^2}$
$latex A=\pi(64)$
$latex A=201.1$
$latex p=2\pi r$
$latex p=2\pi (8)$
$latex p=50.3$
Entonces, el área del círculo es 201.1 m² y el perímetro es 50.3 m.
Ejercicios de área y perímetro de figuras geométricas para resolver
Resuelve los siguientes ejercicios usando lo aprendido sobre el área y el perímetro de figuras geométricas. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
