El volumen de figuras geométricas es una de las medidas más importantes de figuras tridimensionales. El volumen es una medida del espacio ocupado por un objeto en el espacio tridimensional. Dado que el volumen es una medida tridimensional, usamos unidades cúbicas para medirlo. La fórmula del volumen depende de la forma de la figura y de sus diferentes dimensiones.
A continuación, conoceremos las fórmulas de las figuras tridimensionales más importantes. Luego, usaremos estas fórmulas para resolver algunos ejercicios.
Definición del volumen
El volumen de una figura geométrica es definido como la cantidad de espacio ocupado por el objeto o figura en el espacio tridimensional. El volumen es medido en unidades cúbicas, por ejemplo, m³, cm³, etc. El volumen puede ser considerado como la capacidad de un contenedor para mantener una cantidad de fluido (gas o líquido).
El volumen puede ser calculado usando aritmética al multiplicar sus varias dimensiones y, en ciertos casos, usar algunas constantes. Dos figuras geométricas pueden tener el mismo volumen dependiendo en sus dimensiones y su forma.
Fórmulas del volumen de figuras geométricas
La fórmula del volumen de figuras geométricas depende de la forma y de las dimensiones de la figura. Existe una gran cantidad de figuras geométricas tridimensionales, sin embargo, las más importantes son el cubo, el prisma rectangular, el cilindro, la esfera, la pirámide y el tetraedro.
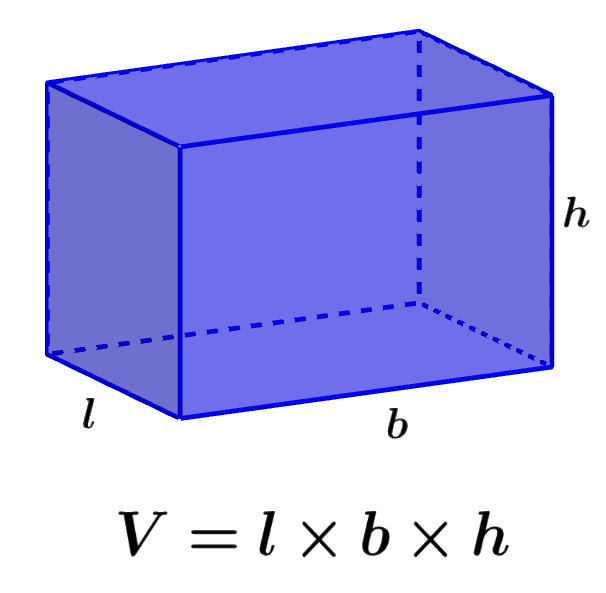
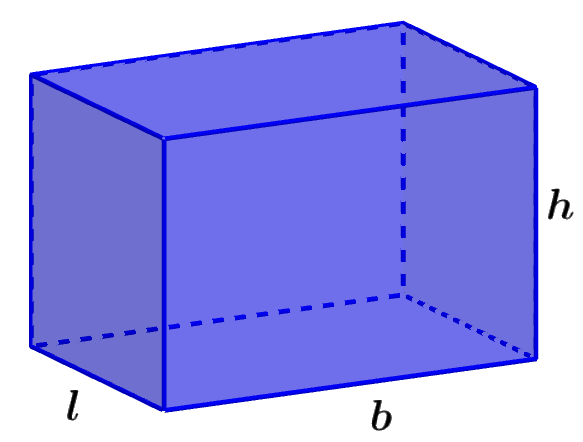
Volumen de un prisma rectangular
Un prisma rectangular es un prisma con bases rectangulares y con caras laterales rectangulares. El volumen de estos prismas depende de sus tres dimensiones.
Fórmula del Volumen= lbh
en donde, l es la longitud del ancho del prisma y b es la longitud de la base y h es la longitud de la altura.
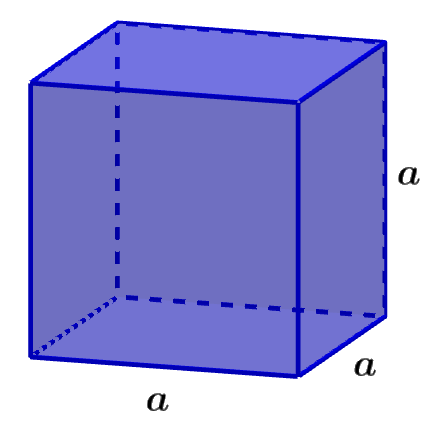
Volumen de un cubo
Un cubo es una figura tridimensional que tiene todos sus lados con la misma longitud. Un cubo tiene un total de seis caras cuadradas.
Fórmula del Volumen = a³
en donde, a es la longitud de uno de los lados del cubo.
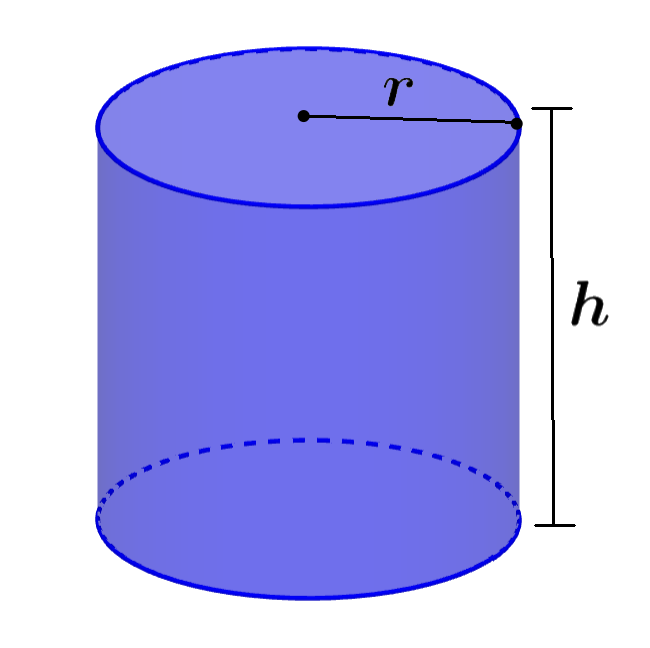
Volumen de un cilindro
Un cilindro se caracteriza por tener dos bases circulares y una superficie que une a las dos bases.
Fórmula del volumen = πr2h
en donde, r es el radio de las bases y h es la altura del cilindro.
Volumen de una esfera
Una esfera es una figura tridimensional completamente redonda. La esfera está definida por el radio.
Fórmula del Volumen = (4⁄3)πr3
en donde, r representa al radio de la esfera y π es una constante matemática con un valor de 3.1415…
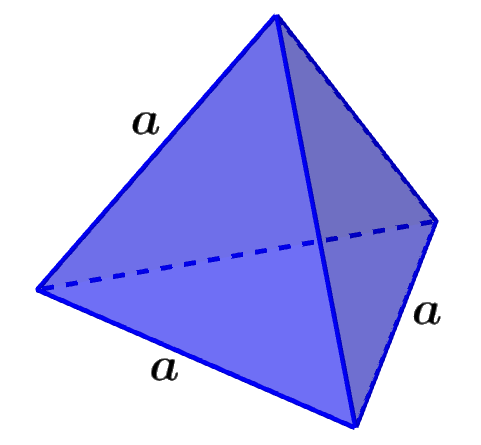
Volumen de un tetraedro
Un tetraedro es una figura tridimensional que tiene cuatro caras triangulares.
Fórmula del Volumen = $latex \frac{{{a}^3}}{6\sqrt{2}}$
en donde, a es la longitud de uno de los lados del tetraedro.
Tabla de fórmulas de volumen de figuras geométricas
| Figura | Volumen |
| Prisma rectangular | V = lbh |
| Cubo | V = a³ |
| Cilindro | V = πr²h |
| Prisma | V = Bh |
| Esfera | V = (4⁄3)πr3 |
| Pirámide | V = (1⁄3) Bh |
| Cono circular | V = (1⁄3)πr2h |
| Tetraedro | V = $latex \frac{{{a}^3}}{6\sqrt{2}}$ |
en donde, r es el radio, a y l representan a las diferentes longitudes de las figuras, h representa a la altura y B representa al área de la base.
Ejercicios de volumen de figuras geométricas resueltos
Las fórmulas del volumen de figuras tridimensionales son usadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde puedes mirar el proceso usado.
EJERCICIO 1
Si es que un cubo tien lados de longitud de 10 m, ¿cuál es su volumen?
Solución
El volumen de un cubo es encontrado al elevar al cubo a la longitud de uno de sus lados. Entonces, tenemos:
$latex V={{a}^3}$
$latex V={{10}^3}$
$latex V=1000$
Entonces, el volumen del cubo es 1000 m³.
EJERCICIO 2
Un cilindro tiene bases con radio de 5 m y una altura de 6 m. ¿Cuál es su volumen?
Solución
Podemos reconocer las dimensiones $latex r=5$ y $latex h=6$. Entonces, usando la fórmula del volumen con estas dimensiones, tenemos:
$latex V=\pi {{r}^2}h$
$latex V=\pi {{(5)}^2}(6)$
$latex V=\pi (25)(6)$
$latex V=471.2$
Entonces, el volumen del cilindro es 471.2 m³.
EJERCICIO 3
¿Cuál es el volumen de una esfera que tiene un radio de 8 m?
Solución
Usamos la fórmula del volumen de la esfera con el radio dado. Entonces, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(8)}^3}$
$latex V=2144.7$
Entonces, el volumen de la esfera es 2144.7 m³.
EJERCICIO 4
¿Cuál es el volumen de un tetraedro que tiene lados de longitud 5 m?
Solución
Usamos la longitud dada en la fórmula del volumen de un tetraedro:
$latex V=\frac{{{a}^3}}{6\sqrt{2}}$
$latex V=\frac{{{5}^3}}{6\sqrt{2}}$
$latex V=\frac{125}{6\sqrt{2}}$
$latex V=14.7$
El volumen del tetraedro es 14.7 m³.
Ejercicios de volumen de figuras geométricas para resolver
Aplica las fórmulas del volumen de figuras tridimensionales para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
