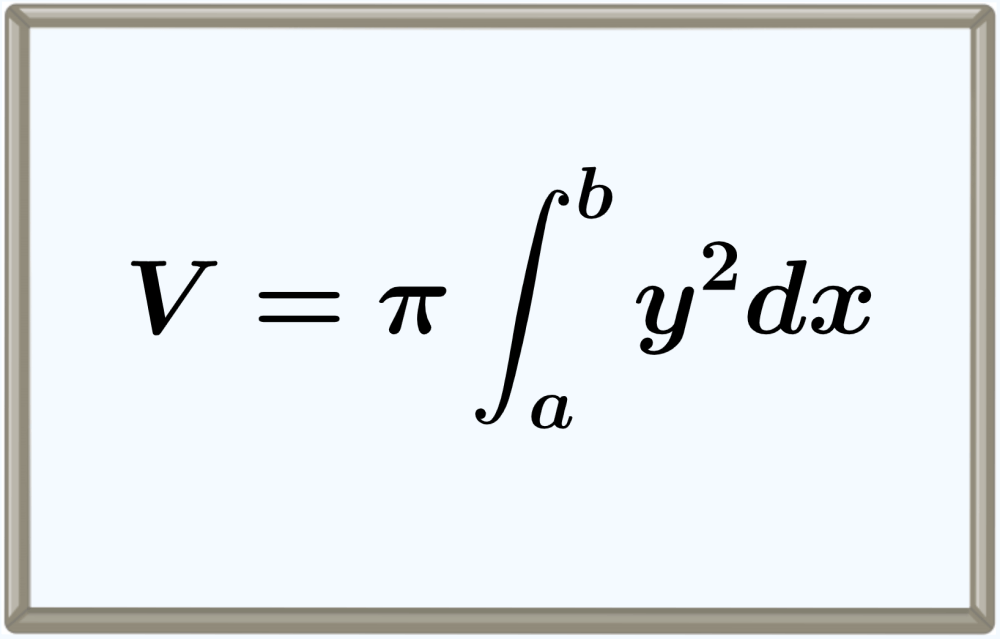El volumen de revolución con respecto al eje x puede ser encontrado al evaluar una integral definida con respecto al cuadrado de la ecuación de la curva y multiplicar el resultado por π. Podemos derivar una fórmula para calcular este volumen usando límites e integrales.
En este artículo, conoceremos cómo calcular el volumen de revolución con respecto al eje x. Aprenderemos a derivar su fórmula y la usaremos en algunos ejemplos prácticos.
Cómo encontrar el volumen de revolución con respecto al eje x
Para encontrar el volumen de revolución de un sólido con respecto al eje x, podemos aplicar la siguiente fórmula:
$$V=\pi \int_{a}^{b} y^2 d x$$
Entonces, podemos seguir el siguiente proceso para usar la fórmula correctamente:
1. Encontrar el cuadrado de la ecuación de la curva que forma el volumen de revolución.
Es decir, empezamos encontrando $latex y^2$.
2. Encontrar el valor de la integral definida $latex \int_{a}^{b} y^2 d x$.
Para esto, reemplazamos la expresión para $latex y^2$ del paso 1.
3. Multiplicar el resultado del paso 2 por π para encontrar el volumen del sólido formado.
Si necesitas hacer una revisión sobre cómo resolver integrales definidas, puedes visitar nuestro artículo: Cómo calcular integrales definidas.
Derivación de la fórmula del volumen de revolución con respecto al eje x
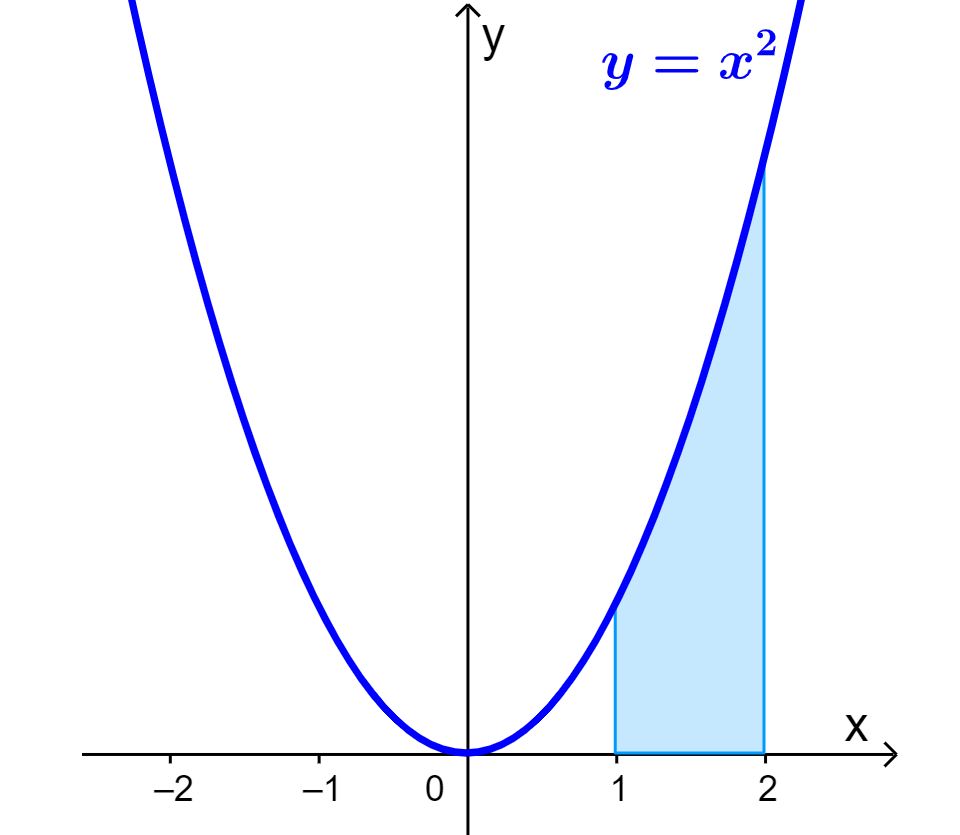
Para encontrar una fórmula para el volumen de revolución con el eje x, empezamos considerando el área bajo la curva $latex y=x^2$ desde $latex x=1$ hasta $latex x=2$, como se muestra en el diagrama:
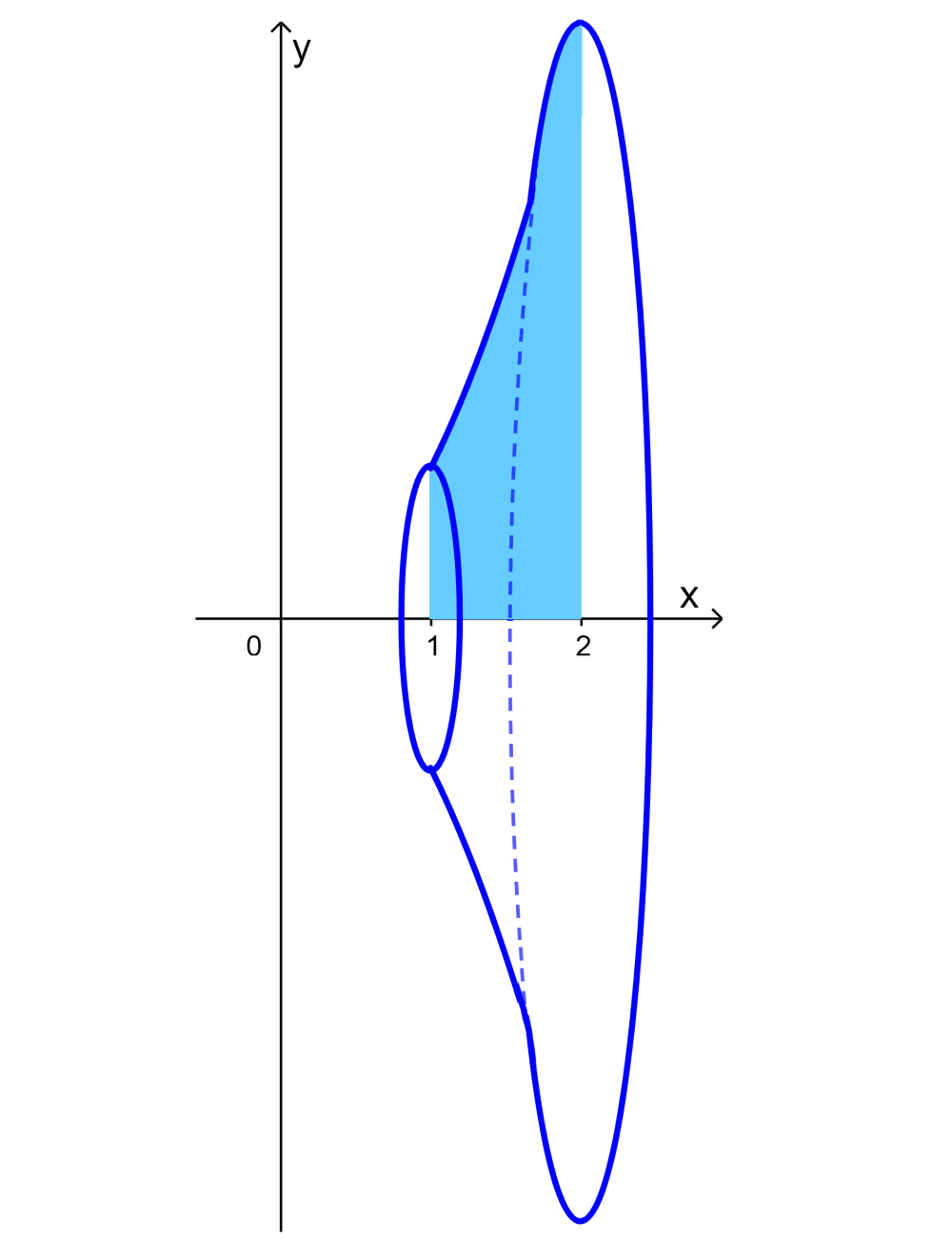
Ahora, consideramos al sólido formado cuando esta área es rotada 2π radianes alrededor del eje x, como se muestra en el siguiente diagrama. Podemos calcular su volumen usando cálculo integral.
Tomamos una tira muy pequeña de longitud $latex \delta x$ bajo la curva $latex f(x)$, como se muestra en el siguiente diagrama:
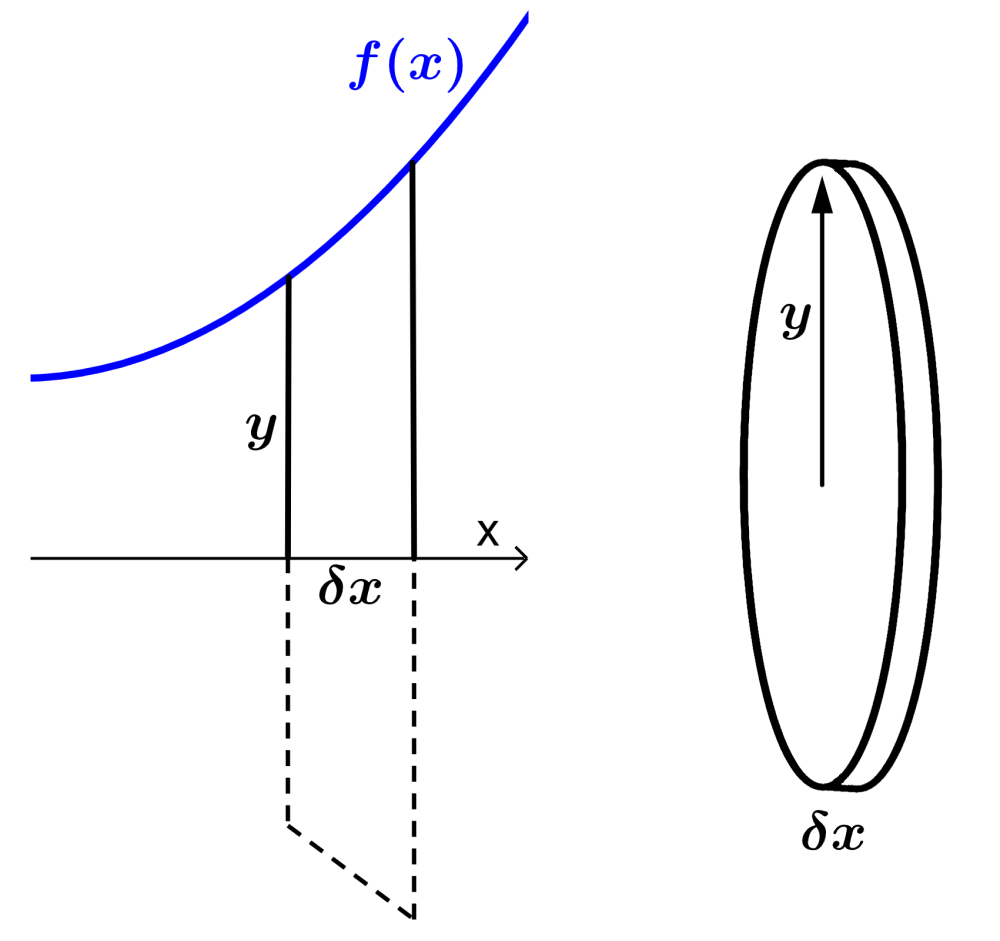
Cuando esta área pequeña es rotada por 2π radianes alrededor del eje x, formamos un disco con un radio igual a $latex y$ y un ancho de $latex \delta x$. El volumen de este disco es:
$latex \delta V= \pi y^2 \delta x$
Para encontrar el volumen de todo el sólido, tenemos que encontrar la suma de todos los discos desde $latex x=a$ hasta $latex x=b$. Entonces, tenemos:
$$V=\sum_{x=a}^{b}\pi y^2 \delta x$$
A medida que $latex \delta \to 0$, esta sumatoria se acerca al valor de $latex V$, por lo que tenemos:
$$V=\lim_{\delta x \to 0} \pi \sum_{x=a}^{b} y^2 \delta x$$
lo cual es igual a
$$V=\pi \int_{a}^{b} y^2 d x$$
Ejercicios resueltos del volumen de revolución con respecto al eje x
EJERCICIO 1
Encuentra el volumen generado cuando el área bajo $latex y=x$ desde $latex x=0$ hasta $latex x=6$ es rotada con respecto al eje x.
Solución
Empezamos escribiendo la fórmula del volumen de revolución:
$$V=\pi \int_{a}^{b} y^2 d x$$
Ahora, sustituimos la expresión para $latex y $, la elevamos al cuadrado y resolvemos la integral definida:
$$V=\pi \int_{0}^{6} x^2 d x$$
$$=\pi \left[ \frac{x^3}{3} \right]_{0}^{6}$$
$$=\pi \left( \frac{216}{3} \right)-(0)$$
$latex V=72 \pi $
EJERCICIO 2
¿Cuál es el volumen generado cuando el área bajo $latex y=x^2$ desde $latex x=0$ hasta $latex x=5$ es rotada con respecto al eje x?
Solución
La fórmula del volumen de revolución con respecto al eje x es:
$$V=\pi \int_{a}^{b} y^2 d x$$
En este caso, tenemos $latex y=x^2$, por lo que sustituimos en la fórmula y evaluamos la integral definida:
$$V=\pi \int_{0}^{5} x^4 d x$$
$$=\pi \left[ \frac{x^5}{5} \right]_{0}^{5}$$
$$=\pi \left( \frac{3125}{5} \right)-(0)$$
$latex V=625 \pi $
EJERCICIO 3
Encuentra el volumen del sólido formado cuando el área bajo $latex y=x^2+2$ desde $latex x=1$ hasta $latex x=3$ es rotada con respecto al eje x.
Solución
El volumen del sólido está dado por la siguiente fórmula:
$$V=\pi \int_{a}^{b} y^2 d x$$
Al elevar a $latex y $ al cuadrado, tenemos $latex y^2=(x^2+2)^2$, lo cual es igual a $latex y^2=x^4+4x^2+4$. Entonces, tenemos:
$$V=\pi \int_{1}^{3} (x^4+4x^2+4) d x$$
$$=\pi \left[ \frac{x^5}{5} + \frac{4x^3}{3}+4x \right]_{1}^{3}$$
$$=\pi \left( \frac{483}{5}- \frac{83}{15} \right)$$
$$ V=\frac{1366 \pi}{15} $$
EJERCICIO 4
Encuentra el volumen de revolución del área bajo $latex y=3\sqrt{x}$ desde $latex x=2$ hasta $latex x=4$ con respecto al eje x.
Solución
Empezamos con la siguiente fórmula para encontrar el volumen:
$$V=\pi \int_{a}^{b} y^2 d x$$
Cuando elevamos a $latex y $ al cuadrado, tenemos $latex y^2=9x$. Entonces, usamos esto en la fórmula para resolver la integral definida:
$$V=\pi \int_{2}^{4} 9x d x$$
$$=\pi \left[ \frac{9x^2}{2} \right]_{2}^{4}$$
$latex =\pi (72 )-( 18)$
$latex V=54\pi $
EJERCICIO 5
Encuentra el volumen de revolución cuando el área bajo $latex y=\sqrt{x^2+3x}$ desde $latex x=2$ y $latex x=6$ es rotado en el eje x.
Solución
Empezamos escribiendo la fórmula del volumen de revolución con el eje x:
$$V=\pi \int_{a}^{b} y^2 d x$$
Cuando elevamos a $latex y $ al cuadrado, tenemos $latex y^2=(\sqrt{x^2+3x})^2$, lo cual es igual a $latex y^2=x^2+3x$. Entonces, tenemos:
$$V=\pi \int_{2}^{6} (x^2+3x) d x$$
$$=\pi \left[ \frac{x^3}{3} + \frac{3x^2}{2} \right]_{2}^{6}$$
$$=\pi [72 + 54 ]-\left[ \frac{8}{3} + 6 \right]$$
$$=\pi \left( \frac{352}{3} \right)$$
$$ V=\frac{352\pi}{3} $$
EJERCICIO 6
El área encerrada entre la curva $latex y=4-x^2$ y la recta $latex y=4-2x$ es rotada con respecto al eje x. Encuentra el volumen del sólido generado.
Solución
En este caso, tenemos un área entre dos curvas. Entonces, podemos trazar una gráfica simple para visualizar esa área:
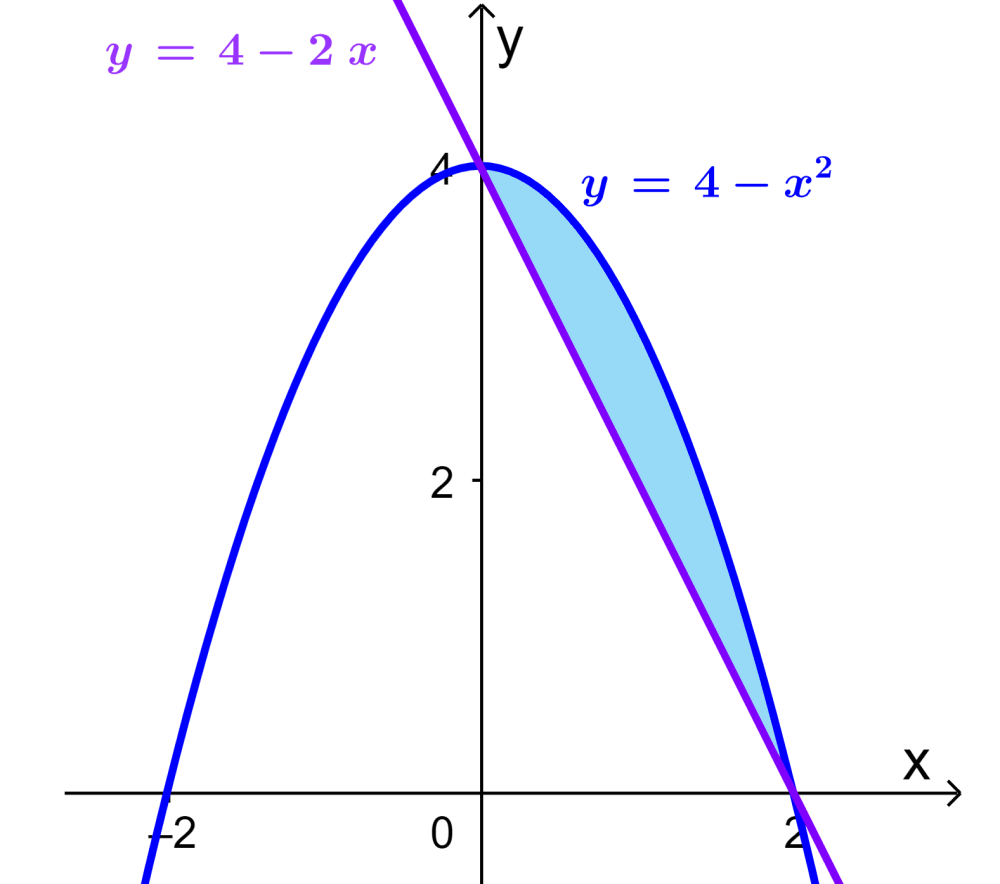
Ahora, podemos ver que el área a ser rotada es un área entre dos curvas. Por lo que resolvemos de la siguiente forma:
$$V=\pi \int_{0}^{2} (4-x^2)^2 d x-\pi \int_{0}^{2} (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (4-x^2)^2 – (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (x^4-12x^2+16x) d x$$
$$=\pi \left[ \frac{x^5}{5}-4x^3+8x^2 \right]_{0}^{2}$$
$$=\pi \left[ \frac{32}{5}-32+32 \right]-[0]$$
$latex V=\frac{32\pi}{5} $
Volumen de revolución con respecto al eje x – Ejercicios para resolver
¿Cuál es el volumen de revolución del área bajo $latex y=\sqrt{3x^2+8}$ desde $latex x=1$ hasta $latex x=3$ con respecto al eje x?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
