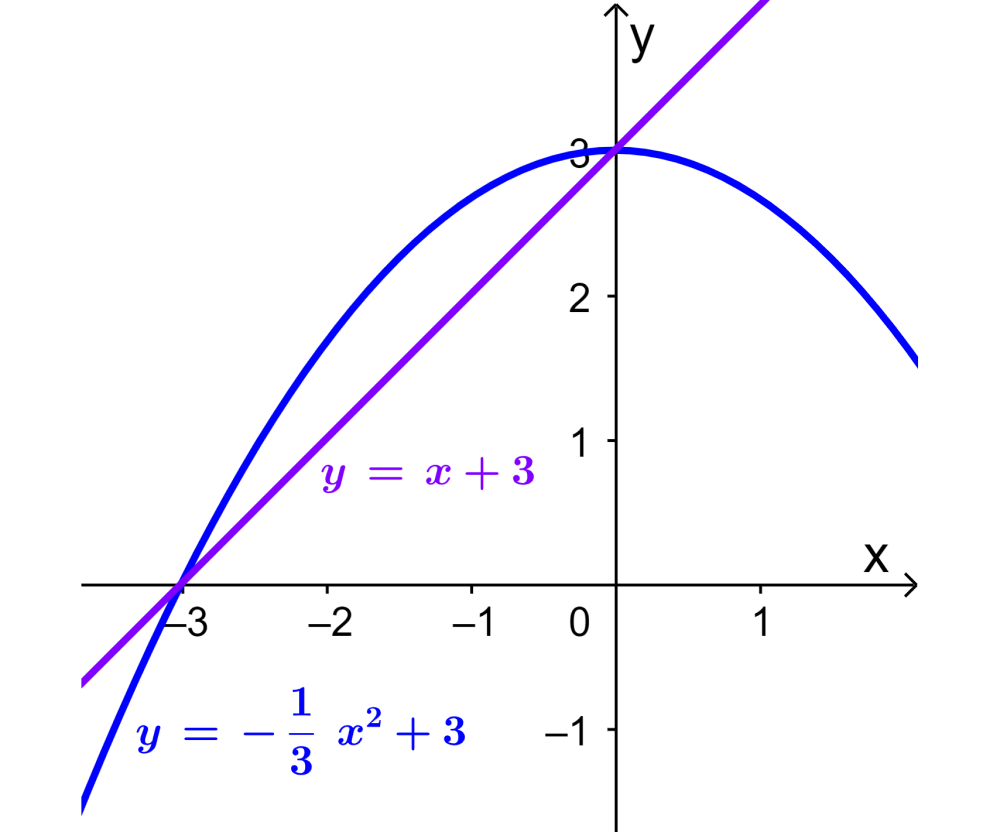Podemos encontrar el área entre dos curvas al encontrar el área bajo cada curva separadamente. Luego, podemos restar estas áreas de modo que obtengamos el área de intersección. Podemos aplicar este principio no solamente con curvas, sino también con los ejes del plano.
A continuación, veremos algunos ejercicios resueltos del área entre dos curvas. Luego, veremos algunos ejercicios en los que puedes practicar lo aprendido.
Cómo encontrar el área entre dos curvas
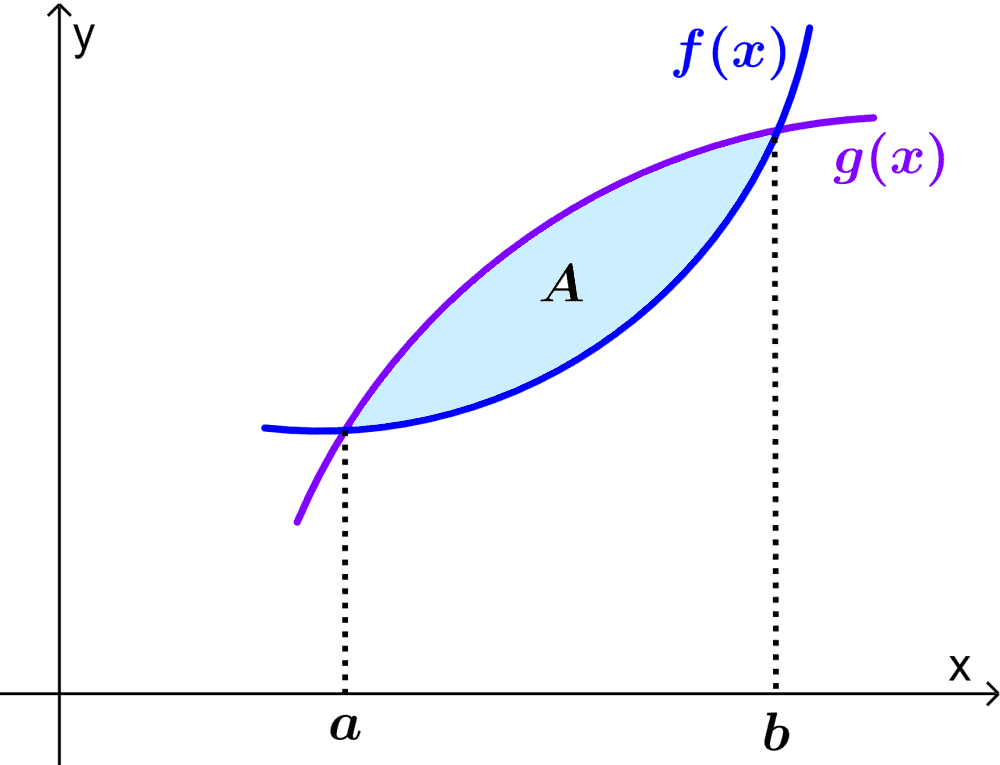
Consideremos a dos curvas intersecantes, $latex f(x)$ y $latex g(x)$, como se muestra en el siguiente diagrama.
Podemos encontrar el área de la región coloreada, es decir, la región de intersección, al restar una curva de la otra, de modo que la diferencia sea igual al área de intersección.
En este caso, el área entre las curvas es obtenida al restar al área bajo la curva $latex f(x)$ del área bajo la curva $latex g(x)$. Es decir, tenemos lo siguiente:
$$A=\int_{a}^{b} g(x)dx-\int_{a}^{b} f(x)dx$$
$$A=\int_{a}^{b} (g(x)-f(x))dx$$
Este principio puede ser aplicado para encontrar el área entre dos o más curvas, rectas o ejes.
Ejercicios resueltos del área entre dos curvas
EJERCICIO 1
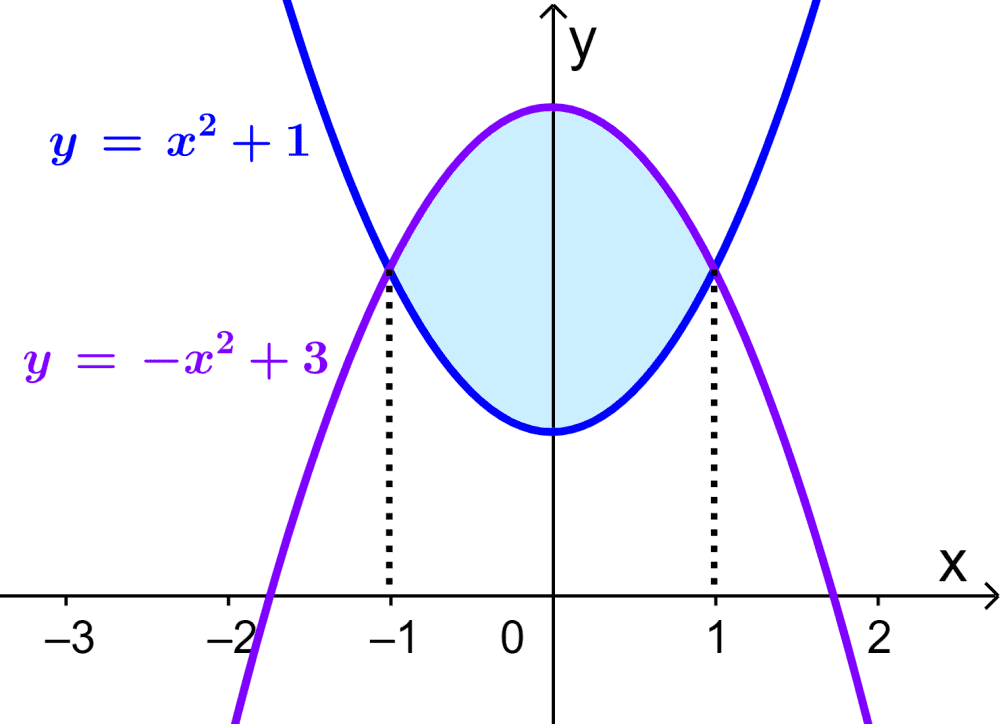
Si es que tenemos las curvas $latex y=x^2+1$ y $latex y=-x^2+3$, ¿cuál es el área de la región de intersección?
Solución
Podemos empezar encontrando los puntos de intersección de las curvas para determinar los límites de la región. Entonces, tenemos:
$latex x^2+1=-x^2+3$
$latex 2x^2=2$
$latex x=\pm 1$
Podemos trazar una gráfica para visualizar el área requerida:
El área de la región puede ser obtenida restando el área bajo la curva $latex y=x^2+1$ del área bajo la curva $latex y=-x^2+3$. Entonces, tenemos:
$$A=\int_{-1}^{1} (-x^2+3) dx-\int_{-1}^{1} (x^2+1) dx$$
$$=\int_{-1}^{1} (-x^2+3) – (x^2+1) dx$$
$$=\int_{-1}^{1} (-2x^2+2) dx$$
$$=\left[ -\frac{2x^3}{3}+2x \right]_{-1}^{1}$$
$$=\left[ -\frac{2}{3}+2 \right]-\left[ \frac{2}{3}-2 \right]$$
$$=\frac{4}{3}+\frac{4}{3}$$
$$=\frac{8}{3}$$
El área de la región de intersección de las dos curvas es $latex \frac{8}{3}$.
EJERCICIO 2
¿Cuál es el área formada por la intersección de $latex y=-\frac{1}{3}x^2+3$ y la recta $latex y=x+3$?
Solución
Similar al ejercicio anterior, tenemos que empezar encontrando los puntos de intersección de la recta y la curva. Entonces, tenemos:
$latex x+3=-\frac{1}{3}x^2+3$
$latex \frac{1}{3}x^2+x=0$
$latex x(\frac{1}{3}x+1)=0$
$latex x=-3~~$ o $latex ~~x=0$
Ahora, podemos trazar una gráfica para visualizar el área requerida:
Entonces, vemos que el área de la región está dada por el área de la recta menos el área de la curva. Es decir, tenemos:
$$A=\int_{-3}^{0} \left(-\frac{1}{3}x^2+3\right)dx-\int_{-3}^{0} (x+3 )dx $$
$$=\int_{-3}^{0} \left(-\frac{1}{3}x^2+3\right) – (x+3)dx$$
$$=\int_{-3}^{0} \left(-\frac{1}{3}x^2-x\right) dx$$
$$=\left[ -\frac{x^3}{9}-\frac{x^2}{2} \right]_{-3}^{0}$$
$$=\left[ -\frac{0^3}{9}-\frac{0^2}{2} \right]-\left[ -\frac{(-3)^3}{9}-\frac{(-3)^2}{2} \right]$$
$$=-\left[ 3-\frac{9}{2} \right]$$
$$=\frac{3}{2}$$
El área de la región de intersección de las dos curvas dadas es 1.5.
EJERCICIO 3
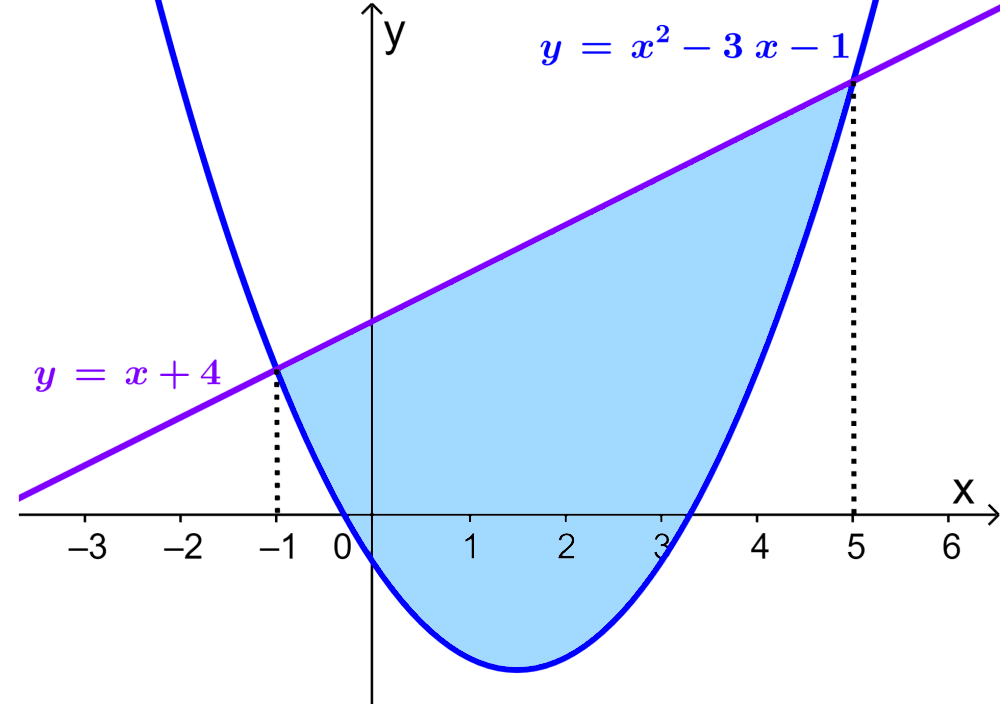
¿Cuál es el área entre la recta $latex y=x+4$ y la curva $latex y=x^2-3x-1$?
Solución
Encontrando los puntos de intersección de la recta y la curva, tenemos:
$latex x+4=x^2-3x-1$
$latex x^2-4x-5=0$
$latex (x-5)(x+1)=0$
$latex x=5~~$ o $latex ~~x=-1$
Cuando trazamos una gráfica, tenemos lo siguiente:
Podemos ver que el área requerida es igual al área bajo la recta menos el área bajo la curva. Entonces, tenemos:
$$A=\int_{-1}^{5} (x+4 )dx-\int_{-1}^{5} (x^2-3x-1) dx$$
$$=\int_{-1}^{5} (x+4)- (x^2-3x-1) dx$$
$$=\int_{-1}^{5} (-x^2+4x+5) dx$$
$$=\left[ -\frac{x^3}{3}+2x^2+5x \right]_{-1}^{5}$$
$$=\left[ -\frac{(5)^3}{3}+2(5)^2+5(5) \right]-\left[ -\frac{(-1)^3}{3}+2(-1)^2+5(-1) \right]$$
$$=\left[ -\frac{125}{3}+50+25 \right]-\left[ \frac{1}{3}+2-5 \right]$$
$$=\frac{100}{3} +\frac{8}{3}$$
$$=\frac{108}{3} $$
$$=36$$
El área entre las dos curvas dadas es 36.
EJERCICIO 4
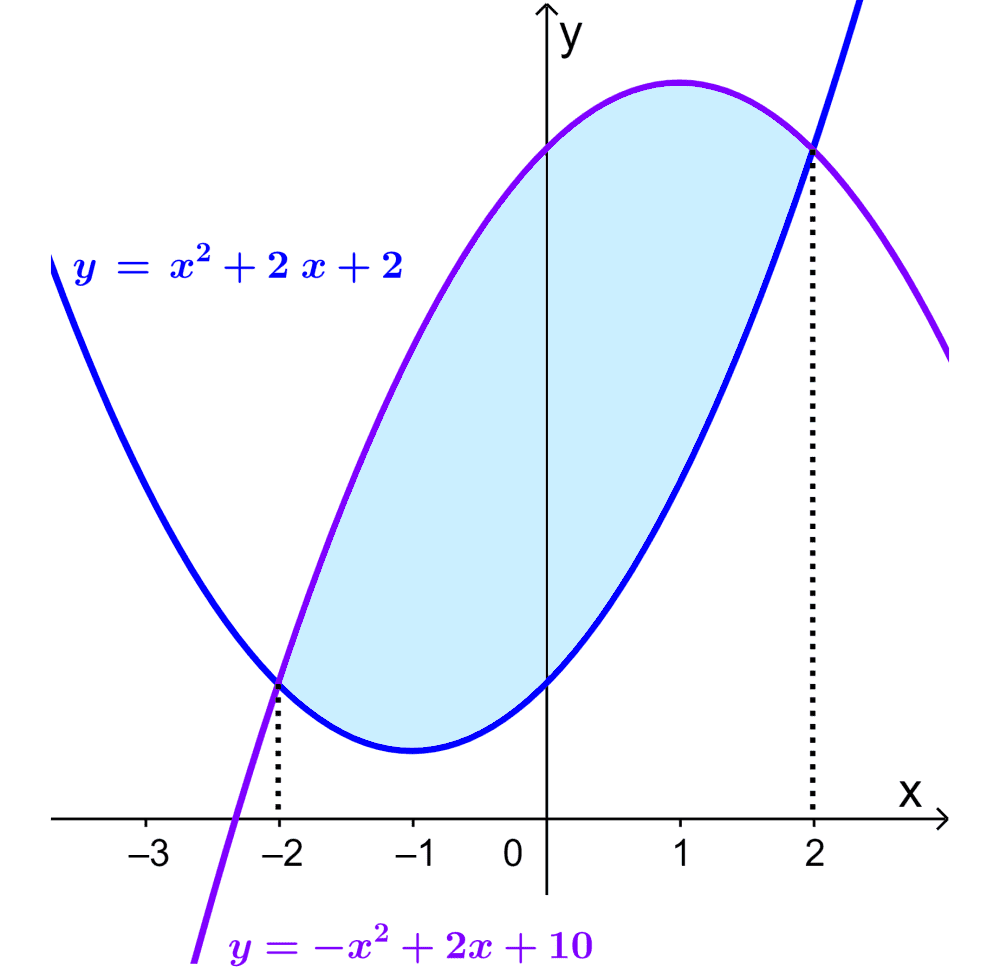
Si es que tenemos las curvas $latex y=x^2+2x+2$ y $latex y=-x^2+2x+10$, ¿cuál es el área de la región de intersección?
Solución
Empezamos encontrando los puntos de intersección:
$$x^2+2x+2=-x^2+2x+10$$
$latex 2x^2-8=2$
$latex x=\pm 2$
Al trazar una gráfica, tenemos:
Podemos encontrar el área de la región requerida de la siguiente forma:
$$A=\int_{-2}^{2} (-x^2+2x+10) dx-\int_{-2}^{2} (x^2+2x+2) dx$$
$$=\int_{-2}^{2} (-x^2+2x+10) – (x^2+2x+2) dx$$
$$=\int_{-2}^{2} (-2x^2+8) dx$$
$$=\left[ -\frac{2x^3}{3}+8x \right]_{-2}^{2}$$
$$=\left[ -\frac{16}{3}-16 \right]-\left[ \frac{16}{3}-16 \right]$$
$$=\frac{32}{3}+\frac{32}{3}$$
$$=\frac{64}{3}$$
El área de la región requerida que se ubica entre las curvas es $latex \frac{64}{3}$.
EJERCICIO 5
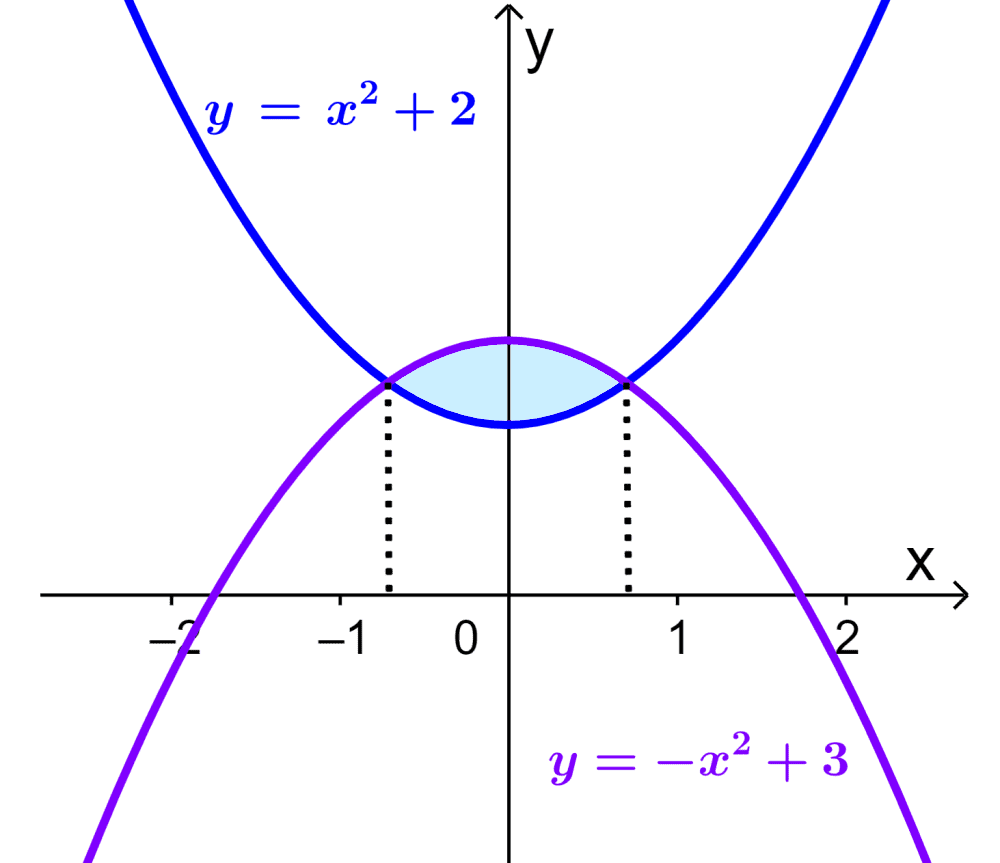
Encuentra el área de la región de intersección de las curvas $latex y=x^2+2$ y $latex y=-x^2+3$.
Solución
Empezamos encontrando los puntos de intersección de las curvas:
$latex x^2+2=-x^2+3$
$latex 2x^2=1$
$latex x=\pm \sqrt{0.5}$
Cuando trazamos una gráfica, tenemos:
Podemos determinar el área de la región requerida de la siguiente forma:
$$A=\int_{-\sqrt{0.5}}^{\sqrt{0.5}} (-x^2+3) dx-\int_{\sqrt{0.5}}^{\sqrt{0.5}} (x^2+2) dx$$
$$=\int_{\sqrt{0.5}}^{\sqrt{0.5}} (-x^2+3) – (x^2+2) dx$$
$$=\int_{\sqrt{0.5}}^{\sqrt{0.5}} (-2x^2+1) dx$$
$$=\left[ -\frac{2x^3}{3}+x \right]_{-\sqrt{0.5}}^{\sqrt{0.5}}$$
$$=\left[ -\frac{\sqrt{0.5}}{3}+\sqrt{0.5} \right]-\left[ \frac{\sqrt{0.5}}{3}-\sqrt{0.5} \right]$$
$$=0.4714+0.4714$$
$$=0.9428$$
El área entre las dos curvas dadas es $latex 0.9428$.
EJERCICIO 6
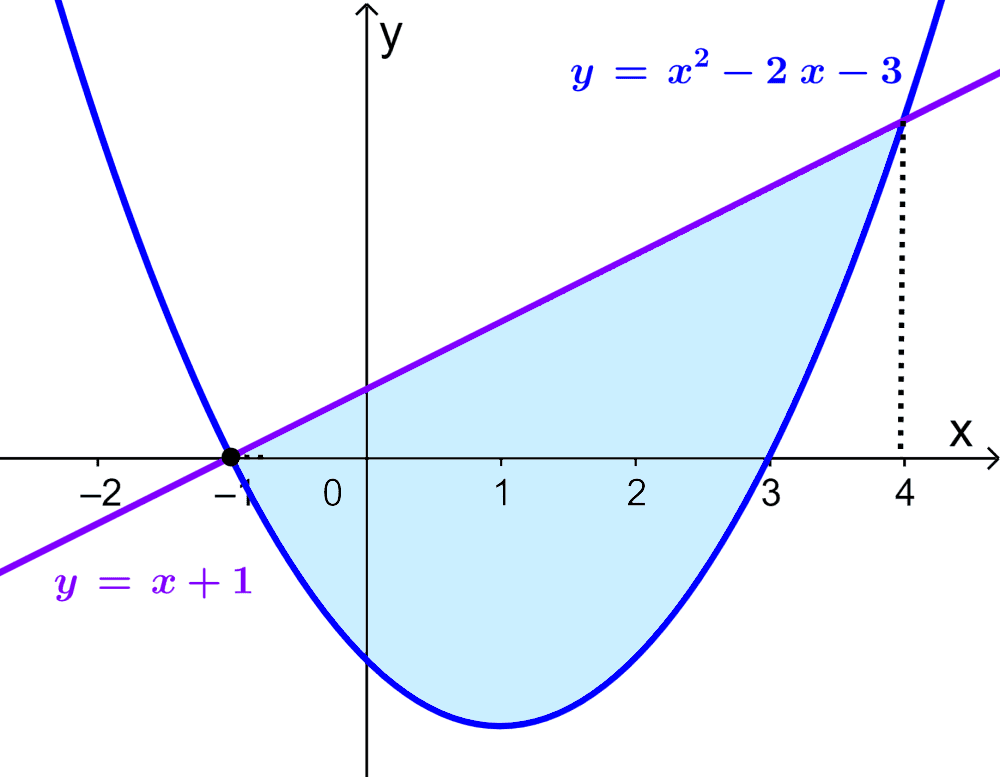
Si es que tenemos la curva $latex y=x^2-2x-3$ y la recta $latex y=x+1$, ¿cuál es el área de la región de intersección?
Solución
Los puntos de intersección son encontrados de la siguiente forma:
$latex x^2-2x-3=x+1$
$latex x^2-3x-4=0$
$latex (x-4)(x+1)=0$
$latex x=4~~$ o $latex ~~x=-1$
Entonces, tenemos la siguiente gráfica:
En este caso, parte del área requerida está bajo el eje x. Sin embargo, el área de la región puede ser calculada usando el mismo método. Entonces, tenemos:
$$A=\int_{-1}^{4} (x+1) dx-\int_{-1}^{4} (x^2-2x-3) dx$$
$$=\int_{-1}^{4} (x+1) – (x^2-2x-3) dx$$
$$=\int_{-1}^{4} (-x^2+3x+4) dx$$
$$=\left[ -\frac{x^3}{3}+\frac{3x^2}{2}+4x \right]_{-1}^{4}$$
$$=\left[ -\frac{64}{3}+24+16 \right]-\left[ \frac{1}{3}+\frac{3}{2}-4 \right]$$
$$=\frac{56}{3}+\frac{13}{6}$$
$$=\frac{125}{6}$$
El área de la región requerida es $latex \frac{125}{6}$.
EJERCICIO 7
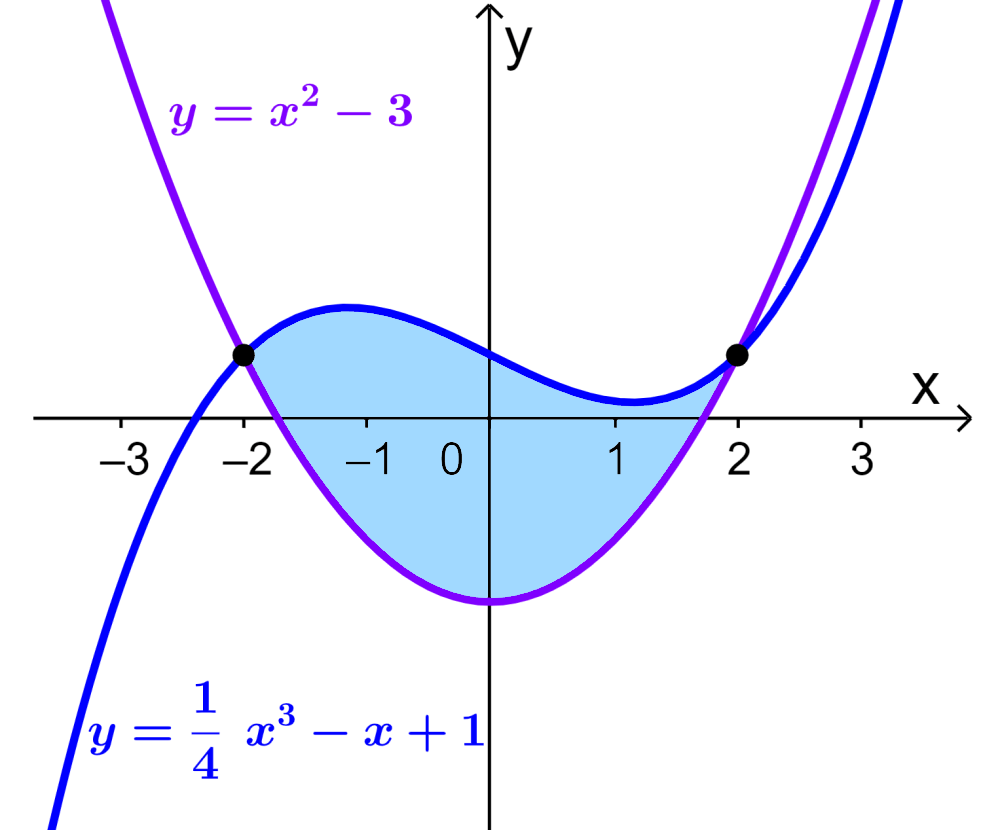
Encuentra el área entre las curvas $latex y=x^2-3$ y $latex y=\frac{1}{4}x^3-x+1$ que va desde $latex x=-2$ hasta $latex x=2$.
Solución
En este caso, no tenemos que encontrar los puntos de intersección, ya que está especificado que tenemos que encontrar el área que va desde $latex x=-2$ hasta $latex x=2$.
Trazando una gráfica, podemos visualizar esta área:
Ahora, vemos que el área requerida está dada por el área de la curva cúbica menos el área de la curva cuadrática:
$$A=\int_{-2}^{2} \left(\frac{1}{4}x^3-x+1\right)dx-\int_{-2}^{2} (x^2-3 )dx $$
$$=\int_{-2}^{2} \left(\frac{1}{4}x^3-x+1\right) – (x^2-3)dx$$
$$=\int_{-2}^{2} \left(\frac{1}{4}x^3-x^2-x+4\right) dx$$
$$=\left[ \frac{x^4}{16}-\frac{x^3}{3}-\frac{x^2}{2}+4x \right]_{-2}^{2}$$
$$=\left[ 1-\frac{8}{3}-2+8 \right]-\left[ 1+\frac{8}{3}-2-8 \right]$$
$$=\frac{13}{3}+\frac{19}{3}$$
$$=\frac{32}{3}$$
El área de la región de intersección de las dos curvas dadas es 10.67.
EJERCICIO 8
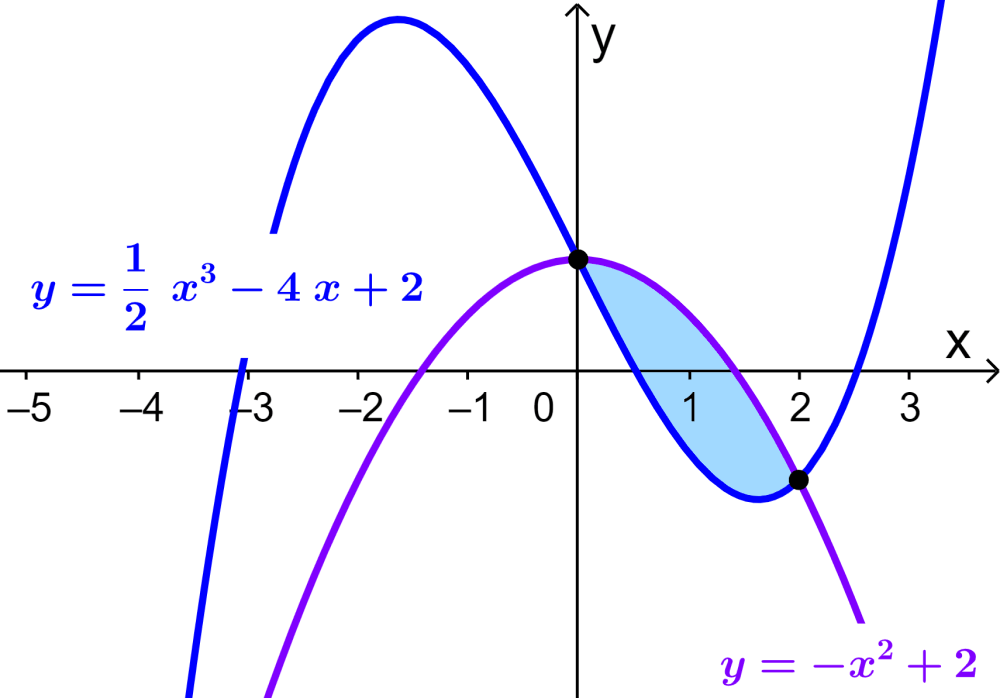
¿Cuál es el área entre las curvas $latex y=-x^2+2$ y $latex y=\frac{1}{2}x^3-4x+2$ que va desde $latex x=0$ hasta $latex x=2$.
Solución
Similar al ejercicio anterior, no tenemos que encontrar los puntos de intersección, ya que conocemos los límites de integración. Entonces, trazando una gráfica, tenemos:
Vemos que el área requerida es igual al área de la curva cuadrática menos el área de la curva cúbica:
$$A=\int_{0}^{2} \left(-x^2+2\right)dx-\int_{0}^{2} \left(\frac{1}{2}x^3-4x+2\right) dx$$
$$=\int_{0}^{2} \left(-x^2+2\right) – \left(\frac{1}{2}x^3-4x+2\right)dx$$
$$=\int_{0}^{2} \left(-\frac{1}{2}x^3-x^2+4x\right) dx$$
$$=\left[ -\frac{x^4}{8}-\frac{x^3}{3}+2x^2 \right]_{0}^{2}$$
$$=\left[ -2-\frac{8}{3}+8 \right]-\left[ 0 \right]$$
$$=\frac{10}{3}$$
El área de la región de intersección de las dos curvas dadas es 3.33.
Ejercicios del área entre dos curvas para resolver
Encuentra el área entre las curvas $latex y=\pm \sqrt{2x+6}$ y $latex y=x-1$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas: