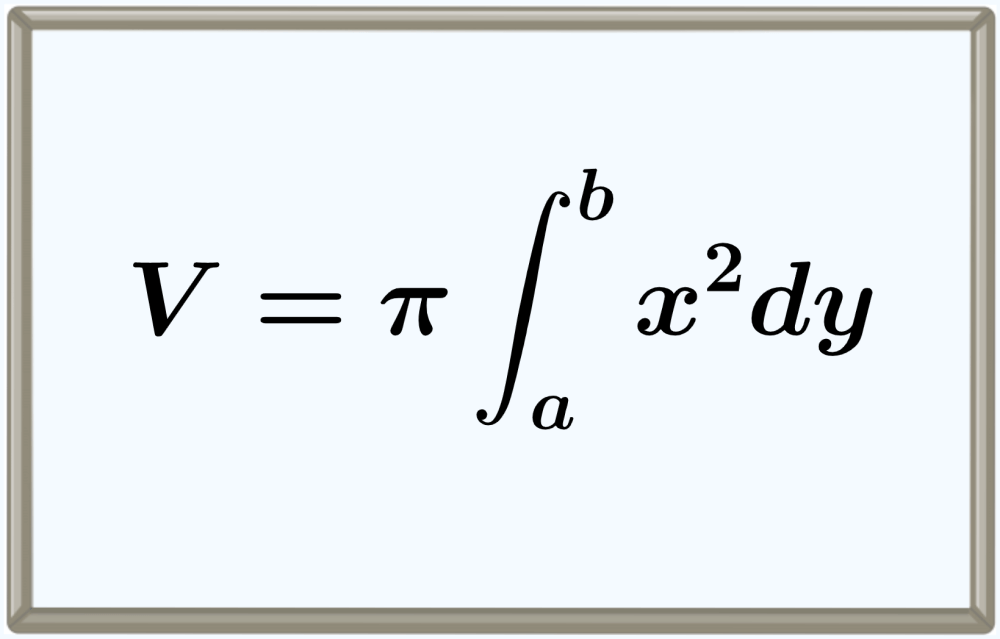El volumen de revolución formado cuando rotamos a un área por 2π con respecto al eje y puede ser encontrado usando una integral definida del cuadrado de la ecuación de la curva y multiplicar el resultado por π. La fórmula para este volumen puede ser derivada usando límites e integrales.
A continuación, aprenderemos cómo calcular el volumen de revolución con respecto al eje y. Conoceremos cómo derivar su fórmula y la aplicaremos en algunos ejemplos.
Cómo encontrar el volumen de revolución con respecto al eje y
El volumen de un sólido de revolución formado al rotar a una área por 2π radianes con respecto al eje y puede ser encontrado en la misma forma que cuando es al respecto del eje x. Entonces, tenemos la siguiente fórmula
$$V=\pi \int_{a}^{b} x^2 d y$$
En este caso, debemos tener en cuenta que $latex dy $ indica que los límites $latex a$ y $latex b$ son límites de $latex y$.
Entonces, seguimos el siguiente proceso para aplicar la fórmula correctamente:
1. Encontramos una expresión para x en términos de y.
Por ejemplo, si $latex y=x^2$, entonces, $latex x=\sqrt{y}$.
2. Elevar al cuadrado a la expresión obtenida en el paso 1.
Es decir, tenemos $latex x^2$.
3. Evaluar la integral definida $latex \int_{a}^{b} x^2 d y$.
Para esto, reemplazamos la expresión para $latex x^2$ del paso 2.
4. Multiplicar por π al resultado del paso 3 para encontrar el volumen del sólido formado.
Puedes hacer una revisión de integrales definidas en este artículo: Cómo calcular integrales definidas.
Ejercicios resueltos del volumen de revolución con respecto al eje y
EJERCICIO 1
Encuentra el volumen generado cuando $latex y=\frac{1}{2}x$ es rotada con respecto al eje y, desde $latex y=0$ hasta $latex y=6$.
Solución
Empezamos recordando la fórmula del volumen de revolución con respecto al eje y:
$$V=\pi \int_{a}^{b} x^2 d y$$
Ahora, tenemos que encontrar una expresión para $latex x $ en términos de y. Podemos lograr esto, resolviendo para x:
$latex y=\frac{1}{2}x$
$latex x=2y$
Sustituimos esta ecuación en la fórmula del volumen y resolvemos la integral definida:
$$V=\pi \int_{0}^{6} (2y)^2 d y$$
$$=\pi \int_{0}^{6} 4y^2 d y$$
$$=\pi \left[ \frac{4y^3}{3} \right]_{0}^{6}$$
$$=\pi \left( \frac{864}{3} \right)-(0)$$
$latex V=288\pi $
EJERCICIO 2
¿Cuál es el volumen generado cuando $latex y=x^2$ es rotada con respecto al eje y, desde $latex y=0$ hasta $latex y=9$?
Solución
La fórmula del volumen de un sólido obtenido al rotar a una curva con el eje y es:
$$V=\pi \int_{a}^{b} x^2 d y$$
Necesitamos una expresión para $latex x $ en términos de y, por lo que la encontramos de la siguiente forma:
$latex y=x^2$
$latex x=\sqrt{y}$
Usando la fórmula del volumen con la expresión encontrada y resolviendo la integral definida, tenemos:
$$V=\pi \int_{0}^{9} (\sqrt{y})^2 d y$$
$$=\pi \int_{0}^{9} y d y$$
$$=\pi \left[ \frac{y^2}{2} \right]_{0}^{9}$$
$$=\pi \left( \frac{81}{2} \right)-(0)$$
$$V=\frac{81\pi}{2} $$
EJERCICIO 3
Si es que tenemos la curva $latex y=x^3$, ¿cuál es el volumen generado al rotarla con respecto al eje y, desde $latex y=1$ hasta $latex y=8$?
Solución
Tenemos la curva $latex y=x^3$. Entonces, $latex x^2$ es igual a:
$latex y=x^3$
$latex x^2=y^{\frac{2}{3}}$
Entonces, cuando sustituimos $latex x^2$ en la fórmula del volumen y resolvemos la integral definida, tenemos:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{1}^{8} y^{\frac{2}{3}} d y$$
$$=\pi \left[ \frac{3y^{\frac{5}{3}}}{5} \right]_{1}^{8}$$
$$=\pi \left[ \frac{3(8)^{\frac{5}{3}}}{5}-\frac{3(1)^{\frac{5}{3}}}{5} \right]$$
$$V=\frac{93\pi}{5} $$
EJERCICIO 4
Encuentra el volumen generado cuando la curva $latex y=\sqrt{x}$ es rotada con respecto al eje y, desde $latex y=0$ hasta $latex y=3$.
Solución
Podemos encontrar una expresión para $latex x$ al elevar a ambos lados de la ecuación al cuadrado:
$latex y=\sqrt{x}$
$latex x=y^2$
Cuando usamos esta expresión en la fórmula del volumen y resolvemos la integral definida, tenemos:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$V=\pi \int_{0}^{3} y^4 d y$$
$$=\pi \left[ \frac{y^5}{5} \right]_{0}^{3}$$
$$=\pi \left( \frac{243}{5}\right)-(0)$$
$$V=\frac{243\pi}{5} $$
EJERCICIO 5
¿Cuál es el volumen generado cuando $latex y=x^4$ es rotada con respecto al eje y, desde $latex y=1$ hasta $latex y=4$?
Solución
En este caso, tenemos la ecuación $latex y=x^4$, por lo que podemos encontrar una expresión para $latex x^2$ sacando la raíz cuadrada de ambos lados:
$latex y=x^4$
$latex x^2=\sqrt{y}$
$latex x^2=y^{\frac{1}{2}}$
Usando esta expresión en la fórmula del volumen, podemos resolver para la integral definida:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{1}^{4} y^{\frac{1}{2}} d y$$
$$=\pi \left[ \frac{2y^{\frac{3}{2}}}{3} \right]_{1}^{4}$$
$$=\pi \left( \frac{16}{3} \right)-\left( \frac{2}{3} \right)$$
$$V= \frac{14\pi}{3} $$
EJERCICIO 6
Encuentra el volumen de revolución de $latex y=x-1$ con respecto al eje x desde $latex y=2$ hasta $latex y=5$.
Solución
Empezamos encontrando una expresión para x en términos de y. Entonces, tenemos:
$latex y=x-1$
$latex x=y+1$
Ahora, usamos esa expresión en la fórmula del volumen de revolución y resolvemos la integral definida:
$$V=\pi \int_{a}^{b} x^2 d y$$
$$=\pi \int_{2}^{5} (y+1)^2 d y$$
$$=\pi \int_{2}^{5} (y^2+2y+1) d y$$
$$=\pi \left[ \frac{y^3}{3}+y^2+y \right]_{2}^{5}$$
$$=\pi \left( \frac{125}{3}+25+5 \right)-\left( \frac{8}{3}+4+2 \right)$$
$$=\pi \left( \frac{215}{3} \right)-\left( \frac{26}{3} \right)$$
$$=\pi \left( \frac{249}{3} \right)$$
$latex V=63\pi $
Volumen de revolución con respecto al eje y – Ejercicios para resolver
Encuentra el volumen del sólido formado al rotar a $latex y=\frac{1}{2}x+3$ con respecto al eje y desde $latex y=4$ y $latex y=6$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
