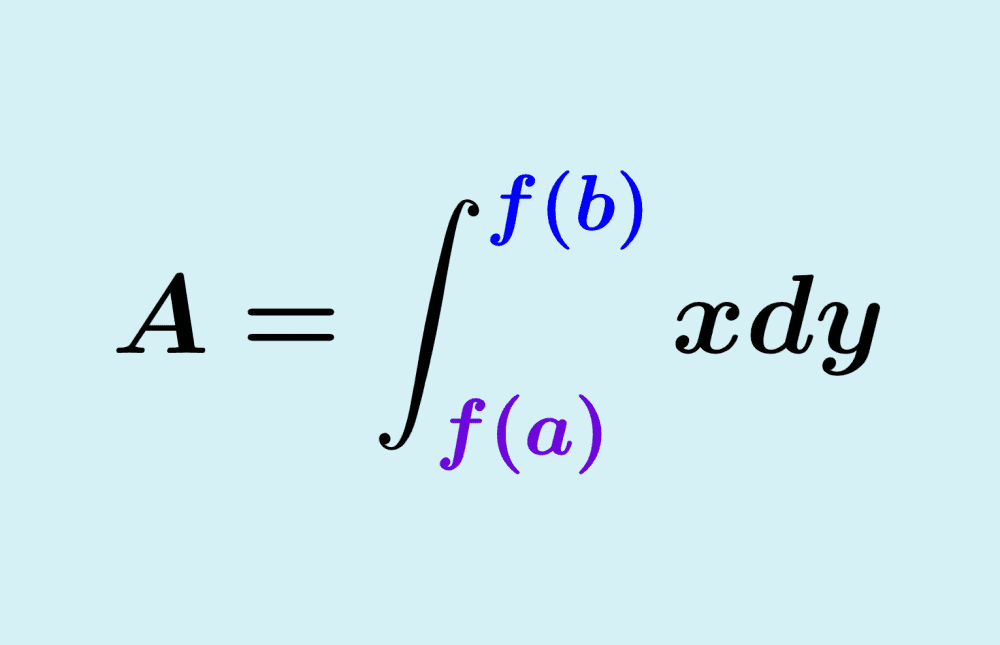El área entre una curva y el eje y puede ser encontrada usando dos métodos principales. El primer método consiste en usar rectángulos y restar sus áreas de modo que obtengamos el área requerida. El segundo método consiste en expresar a x como una función de y para obtener una integral definida.
A continuación, conoceremos los métodos que podemos usar para encontrar el área entre una curva y el eje y. Luego, usaremos estos métodos para resolver algunos ejercicios de práctica.
Encontrar el área entre una curva y el eje y usando rectángulos
Consideremos el área que se muestra en el siguiente diagrama. Esta área está encerrada por la curva $latex y=f(x)$ y el eje y entre $latex y_{1}=f(a)$ y $latex y_{2}=f(b)$.
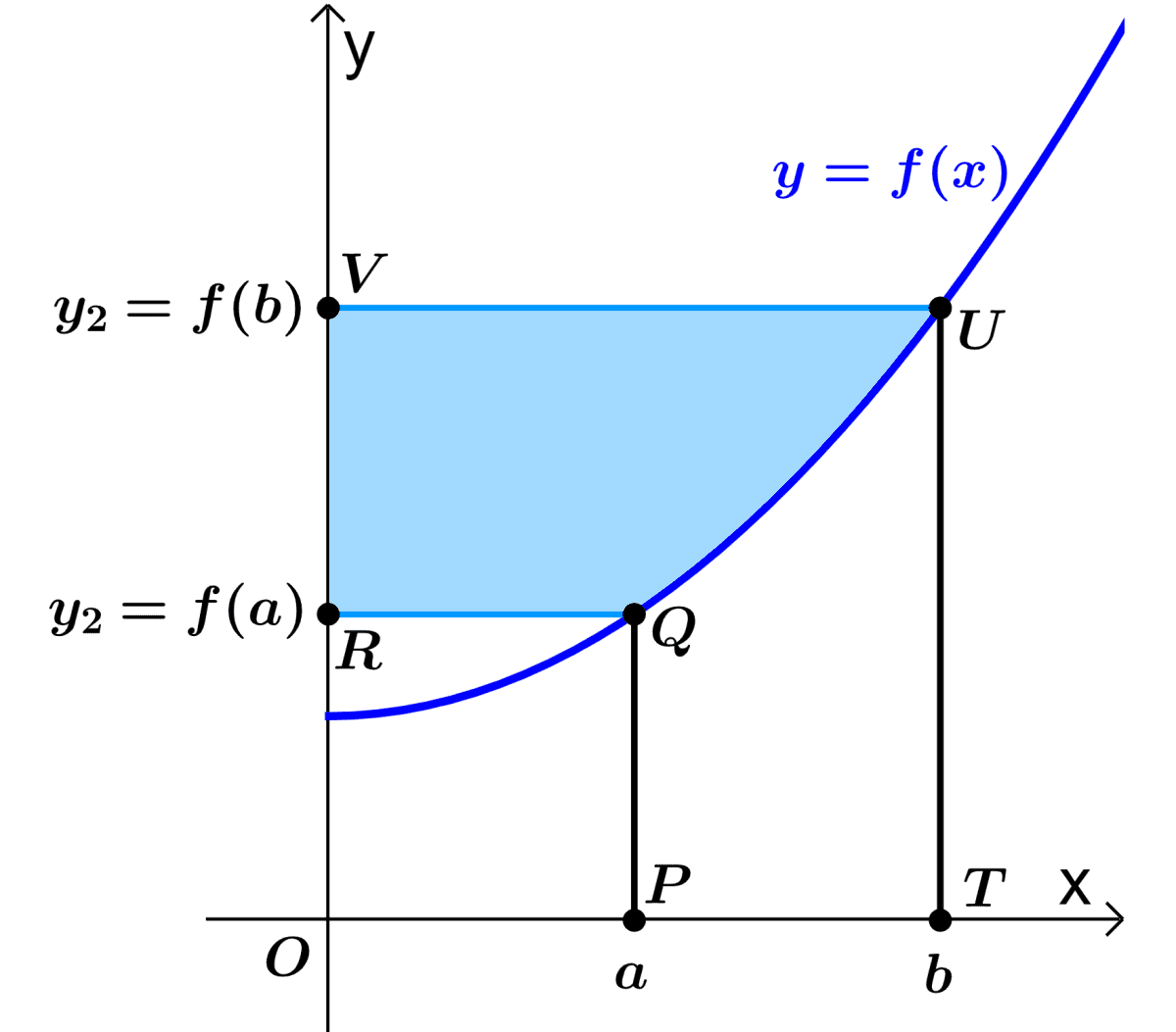
Podemos encontrar esta área usando rectángulos. Entonces, usando el diagrama, podemos determinar que el área $latex A$ es igual a:
$latex A=$(Área de OTUV)$latex -$(Área de OPQR)$latex -$(Área bajo $latex f(x)$ entre $latex x=a$ y $latex x=b$)
Entonces, si es que simplificamos esto, tenemos la siguiente fórmula:
$$A=bf(b)-af(a)-\int_{a}^{b} f(x)dx$$
Encontrar el área entre una curva y el eje y expresando a x como función de y
El área entre una curva y el eje y puede ser calculada al expresar a x como una función de y. Esto significa que tenemos que evaluar lo siguiente:
$$A=\int_{f(a)}^{f(b)} xdy$$
Entonces, consideramos lo siguiente
- $latex dy$ indica que los límites $latex f(a) $ y $latex f(b)$ son límites de y.
- $latex f(a)$ es el límite inferior y es encontrado al usar el valor de $latex a$ en $latex f(x)$. Es decir, encontramos el valor de $latex y_{1}$ del diagrama de arriba.
- $latex f(b)$ es el límite superior y es encontrado al usar el valor de $latex b$ en $latex f(x)$. Es decir, encontramos el valor de $latex y_{2}$.
- $latex x $ es una función de $latex y$. Encontramos esta función al resolver la función original para $latex x$. Por ejemplo, $latex y=3x+1$ se vuelve $latex x=\frac{y-1}{3}$.
Luego, podemos evaluar la integral definida siguiendo los pasos vistos en este artículo.
Ejercicios resueltos del área entre una curva y el eje y
EJERCICIO 1
Encuentra el área entre la curva $latex y=x^2$ y el eje y desde $latex y=1$ y $latex y=4$. Usa rectángulos para resolver.
Solución
Para resolver esto usando rectángulo, podemos observar que el área A está dada por:
$$A=(4\times 2)-(1\times 1)-\int_{1}^{2} x^2 dx$$
Los límites de la integral $latex x=1$ y $latex x=2$ son los equivalentes a $latex y=1$ y $latex y=4$ respectivamente.
Encontrando el valor de la integral definida, tenemos:
$$\int_{1}^{2} x^2 dx=\left[ \frac{x^3}{3} \right]_{1}^{2}$$
$$\int_{1}^{2} x^2 dx=\left[ \frac{8}{3} \right]-\left[ \frac{1}{3} \right]$$
$$\int_{1}^{2} x^2 dx= \frac{7}{3}$$
Entonces, tenemos:
$$A=8-1-\frac{7}{3}$$
$$A=\frac{14}{3}$$
EJERCICIO 2
Usa el segundo método para encontrar el área entre la curva $latex y=x^2$ y el eje y desde $latex y=1$ y $latex y=4$.
Solución
Para usar el segundo método, tenemos que evaluar la siguiente integral definida:
$$A=\int_{1}^{4} x dy$$
Entonces, tenemos que encontrar a x como una función de y. Entonces, tenemos:
$latex y=x^2$
$latex \sqrt{y}=x$
Ahora, sustituimos y resolvemos la integral:
$$\int_{1}^{4} \sqrt{y} dy=\int_{1}^{4} y^{\frac{1}{2}} dy$$
$$=\left[\frac{2y^{\frac{3}{2}}}{3}\right]_{1}^{4}$$
$$=\left[\frac{2(4)^{\frac{3}{2}}}{3}\right]-\left[\frac{2(1)^{\frac{3}{2}}}{3}\right]$$
$$=\frac{16}{3}-\frac{2}{3}$$
$$A=\frac{14}{3}$$
Podemos ver que obtuvimos la misma respuesta que el ejercicio anterior, por lo que ambos métodos son válidos.
EJERCICIO 3
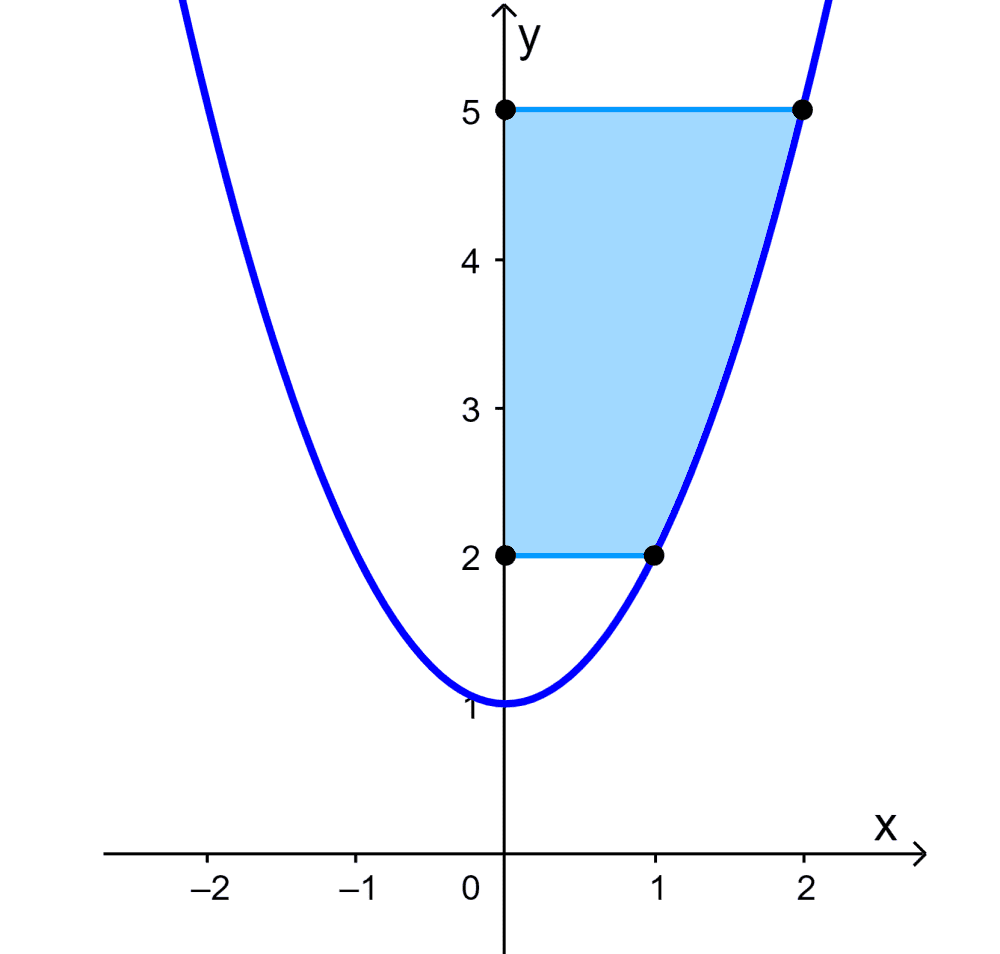
Encuentra el área entre la curva $latex y=x^2+1$ y el eje y desde $latex y=2$ y $latex y=5$ usando el primer método.
Solución
Podemos observar que el área requerida está dada por:
$$A=(5\times 2)-(2\times 1)-\int_{1}^{2} x^2+1 dx$$
Ahora, vamos a encontrar el valor de la integral definida:
$$\int_{1}^{2} x^2+1 dx=\left[ \frac{x^3}{3}+x \right]_{1}^{2}$$
$$=\left[ \frac{8}{3} +2 \right]-\left[ \frac{1}{3} +1 \right]$$
$$= \frac{10}{3}$$
Entonces, tenemos:
$$A=10-2-\frac{10}{3}$$
$$A=\frac{14}{3}$$
EJERCICIO 4
Determina el área entre la curva $latex y=x^2+1$ y el eje y desde $latex y=2$ y $latex y=5$ usando el segundo método.
Solución
Para resolver el ejemplo usando el segundo método, tenemos que resolver la siguiente integral
$$A=\int_{2}^{5} x dy$$
Ahora, vamos a encontrar a una ecuación de x como función de y. Entonces, tenemos:
$latex y=x^2+1$
$latex \sqrt{y-1}=x$
Sustituyendo esta expresión y resolviendo la integral definida, tenemos:
$$\int_{2}^{5} \sqrt{y-1} dy=\int_{2}^{5} (y-1)^{\frac{1}{2}} dy$$
$$=\left[\frac{2}{3}(y-1)^{\frac{3}{2}}\right]_{2}^{5}$$
$$=\left[\frac{2}{3}(5-1)^{\frac{3}{2}}\right]-\left[\frac{2}{3}(2-1)^{\frac{3}{2}}\right]$$
$$=\left[\frac{2}{3}(4)^{\frac{3}{2}}\right]-\left[\frac{2}{3}(1)^{\frac{3}{2}}\right]$$
$$=\left[\frac{2}{3}(8)\right]-\left[\frac{2}{3}(1)\right]$$
$$=\frac{16}{3}-\frac{2}{3}$$
$$A=\frac{14}{3}$$
EJERCICIO 5
Encuentra el área entre la curva $latex y=x^3+1$ y el eje y desde $latex y=1$ y $latex y=4$ usando cualquier método.
Solución
En este caso, el método 2 puede resultar más simple, por lo que vamos a usar ese método. Entonces, tenemos que evaluar la siguiente integral definida:
$$A=\int_{1}^{4} x dy$$
Ahora, encontramos una ecuación para x en términos de y:
$latex y=x^3+1$
$latex \sqrt[3]{y-1}=x$
Podemos sustituir la expresión encontrada y resolver la integral definida:
$$\int_{1}^{4} \sqrt[3]{y-1} dy=\int_{1}^{4} (y-1)^{\frac{1}{3}} dy$$
$$=\left[\frac{3}{4}(y-1)^{\frac{4}{3}}\right]_{1}^{4}$$
$$=\left[\frac{3}{4}(4-1)^{\frac{4}{3}}\right]-\left[\frac{3}{4}(1-1)^{\frac{4}{3}}\right]$$
$$=\left[\frac{3}{4}(4.327)\right]-[0]$$
$$A=3.245$$
Área entre una curva y el eje y – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
