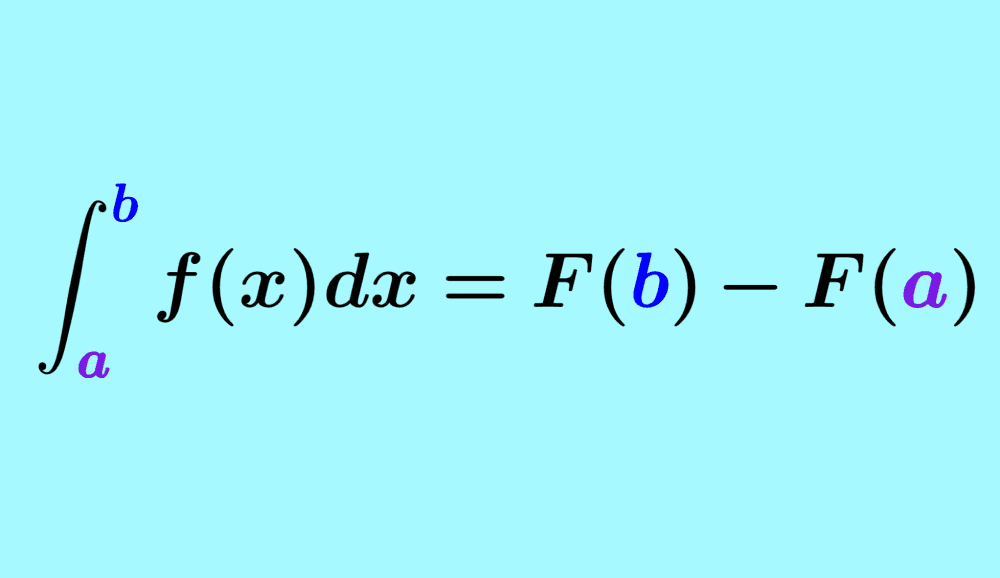Las integrales definidas se caracterizan por resultar en un valor específico o definido. Para encontrar la integral definida de una función, tenemos que evaluar a la integral usando los límites de integración. La integral en el límite inferior es restada de la integral en el límite superior.
A continuación, resolveremos 10 ejercicios de integrales definidas de funciones. Luego, veremos algunos ejercicios prácticos para aplicar todo lo aprendido sobre este tipo de integrales.
Proceso usado para encontrar la integral definida de una función
Supongamos que tenemos la integral $latex F=\int f(x) dx$. Cuando resolvemos esta integral, no obtenemos un valor específico, sino que obtenemos una función de x.
Si es que queremos obtener un valor específico para $latex F$, tenemos que evaluarla en intervalos específicos. Entonces, tenemos:
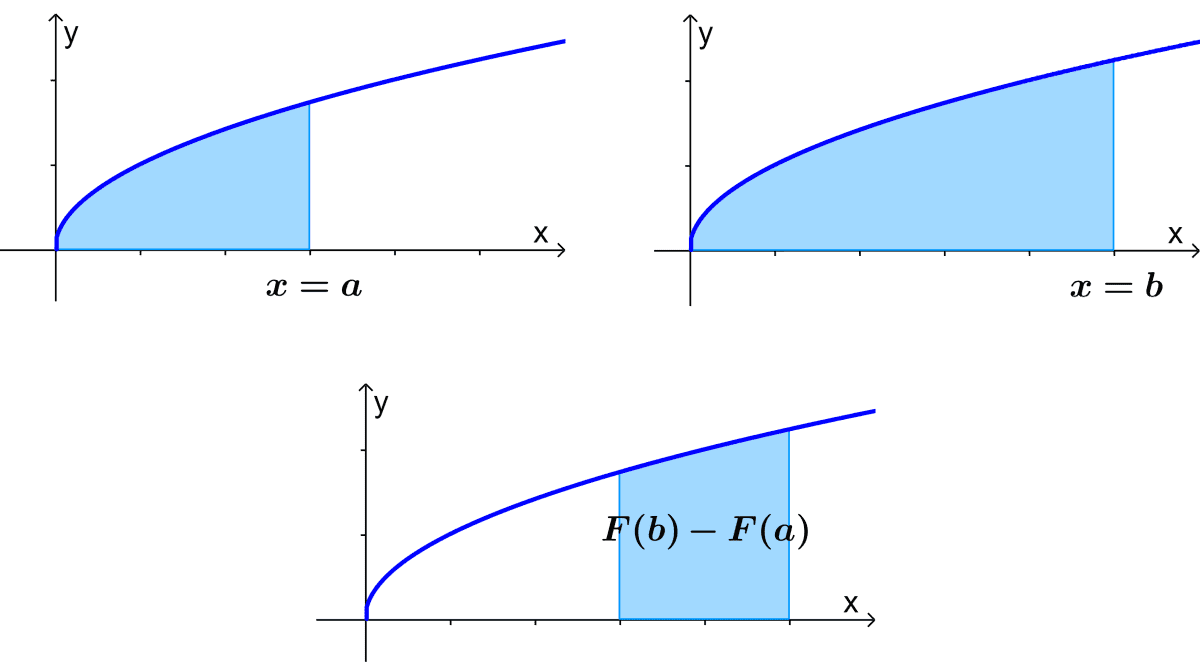
$$ F= (\text{Área hasta }x=b)-(\text{Área hasta }x=a)$$
$latex =F(b)-F(a)$
Esto se escribe como
$$F= \int_{a}^{b} f(x)dx$$
$latex F= \int_{a}^{b} f(x)dx$ es una integral definida, ya que nos da una respuesta definitiva.
- $latex dx$ indica que la función debe integrarse con respecto a x.
- La constante $latex a$ es el límite inferior de la integral.
- La constante $latex b$ es el límite superior de la integral.
Entonces, si es que queremos resolver la integral $latex \int_{0}^{1} 2xdx$, seguimos los siguientes pasos:
Paso 1: Encontrar la integral de la función y usar corchetes para encerrar a la expresión integrada y para expresar los límites de integración. En este caso, tenemos:
$latex \int_{0}^{1} 2xdx=[x^2+c]_{0}^{1}$
Paso 2: Evaluar a la función en sus límites superior e inferior. La función en el límite superior es restada de la función en el límite inferior. Entonces, tenemos:
$latex [x^2+c]_{0}^{1}=[(1)^2+c]-[(0)^2+c]$
Paso 3: Simplificar hasta obtener un único valor numérico:
$latex =[(1)^2+c]-[(0)^2+c]$
$latex =[1+c]-[0+c]$
$latex =1$
Observamos que las constantes de integración fueron canceladas. Por esta razón, es normal excluir las constantes de integración cuando estamos trabajando con integrales definidas.
10 Ejercicios resueltos de integrales definidas
EJERCICIO 1
Encuentra el resultado de la integral definida $latex \int_{0}^{2} 4x^3dx$.
Solución
Para resolver esta integral definida, tenemos que empezar integrando la expresión y usar corchetes para indicar los límites de integración:
$$\int_{0}^{2} 4x^3dx=[x^4+c]_{0}^{2}$$
Ahora, podemos evaluar los límites. La expresión evaluada en el límite inferior es restada de la expresión evaluada en el límite superior:
$$[x^4+c]_{0}^{2}=[(2)^4+c]-[(0)^4+c]$$
Cuando simplificamos esto tenemos:
$latex =[(2)^4+c]-[(0)^4+c]$
$latex =[16+c]-[0+c]$
$latex =16$
Podemos observar que la constante de integración fue eliminada, por lo que podemos omitirla cuando estamos trabajando con integrales definidas.
EJERCICIO 2
Resuelve la integral definida $latex \int_{2}^{3} (6x^2-1) dx$.
Solución
Empezamos encontrando la integral a ser evaluada. Mantenemos los límites de integración usando corchetes e ignoramos la constante de integración:
$$\int_{2}^{3} (6x^2-1)dx=[2x^3-x]_{2}^{3}$$
Ahora que tenemos la integral, podemos evaluarla en los límites dados de la siguiente forma:
$$[2x^3-x]_{2}^{3}=[2(3)^3-(3)]-[2(2)^3-(2)]$$
Por último, simplificamos de la siguiente forma:
$latex =[2(3)^3-(3)]-[2(2)^3-(2)]$
$latex =[54-3]-[16-2]$
$latex =[51]-[14]$
$latex =37$
EJERCICIO 3
Encuentra el valor de la integral $latex \int_{4}^{5} (4x+3)dx$.
Solución
Integrando la expresión dada y manteniendo los límites de integración, tenemos:
$$\int_{4}^{5} (4x+3)dx=[2x^2+3x]_{4}^{5}$$
Evaluando los límites, tenemos:
$$[2x^2+3x]_{4}^{5}=[2(5)^2+3(5)]-[2(4)^2+3(4)]$$
Por último, simplificamos para obtener:
$latex =[2(5)^2+3(5)]-[2(4)^2+3(4)]$
$latex =[50+15]-[32+12]$
$latex =[65]-[44]$
$latex =21$
EJERCICIO 4
¿Cuál es el valor de la integral definida $latex \int_{2}^{3} (4-3x^2)dx$?
Solución
Para encontrar el valor de la integral, tenemos que empezar integrando la expresión mientras mantenemos los límites de integración:
$$\int_{2}^{3} (4-3x^2)dx=[4x-x^3]_{2}^{3}$$
Ahora, vamos a evaluar los límites. Restamos el límite inferior del límite superior:
$$[4x-x^3]_{2}^{3}=[4(3)-(3)^3]-[4(2)-(2)^3]$$
Podemos simplificar para obtener un valor único:
$latex =[4(3)-(3)^3]-[4(2)-(2)^3]$
$latex =[12-27]-[8-8]$
$latex =[-15]-[0]$
$latex =-15$
EJERCICIO 5
Encuentra el resultado de la integral definida $latex \int_{2}^{8} \frac{1}{x^2} dx$.
Solución
Tenemos que empezar encontrando la integral de la expresión dada. En este caso, vamos a usar las leyes de los exponentes para escribir de la siguiente forma:
$$\int_{2}^{8} \frac{1}{x^2} dx=\int_{2}^{8} x^{-2} dx$$
$$=[-x^{-1}]_{2}^{8}$$
Ahora que tenemos la integral, vamos a evaluar los límites:
$$[-x^{-1}]_{2}^{8}=[-(8)^{-1}]-[-(2)^{-1}]$$
Finalmente, simplificamos para obtener un valor definido:
$latex =[-(8)^{-1}]-[-(2)^{-1}]$
$$=-\frac{1}{8}+\frac{1}{2}$$
$$=\frac{3}{8}$$
EJERCICIO 6
Encuentra el valor de la integral $latex \int_{1}^{2} \frac{4}{x^3} dx$.
Solución
Para integral esta expresión, tenemos que usar las leyes de los exponentes para escribirla sin la fracción. Entonces, tenemos:
$$\int_{1}^{2} \frac{4}{x^3} dx=\int_{1}^{2} 4x^{-3} dx$$
$$=[-2x^{-2}]_{1}^{2}$$
Ahora, vamos a evaluar a la expresión dada con los límites de integración dados:
$$[-2x^{-2}]_{1}^{2}=[-2(2)^{-2}]-[-2(1)^{-2}]$$
Cuando simplificamos esto tenemos:
$latex =[-2(2)^{-2}]-[-2(1)^{-2}]$
$$=-\frac{1}{2}+2$$
$$=\frac{3}{2}$$
EJERCICIO 7
Si es que tenemos la integral definida $latex \int_{4}^{9} \sqrt{x} dx$, ¿cuál es su valor?
Solución
En este caso, tenemos una raíz cuadrada. Entonces, la escribimos con un exponente numérico usando las leyes de los exponentes:
$$\int_{4}^{9} \sqrt{x} dx=\int_{4}^{9} x^{\frac{1}{2}} dx$$
$$=\left[\frac{2}{3} x^{\frac{2}{3}}\right]_{4}^{9}$$
Ahora, evaluamos a la expresión usando los límites de integración:
$$=\left[\frac{2}{3} (9)^{\frac{3}{2}}\right]-\left[\frac{2}{3} (4)^{\frac{3}{2}}\right]$$
Podemos simplificar considerando que el exponente $latex \frac{3}{2}$ es equivalente a sacar la raíz cuadrada y elevar el resultado al cubo.
$$=\left[\frac{2}{3} (9)^{\frac{3}{2}}\right]-\left[\frac{2}{3} (4)^{\frac{3}{2}}\right]$$
$$=\left[\frac{2}{3} (27)\right]-\left[\frac{2}{3} (8)\right]$$
$$=18-\frac{16}{3}$$
$$=\frac{38}{3}=12~\frac{2}{3}$$
EJERCICIO 8
Encuentra el resultado de la integral definida $latex \int_{1}^{4} \left( 3- \frac{1}{\sqrt{x}}\right) dx$.
Solución
Empezamos escribiendo a la expresión con un exponente numérico para encontrar su integral:
$$\int_{1}^{4} \left( 3- \frac{1}{\sqrt{x}}\right)dx=\int_{1}^{4} ( 3- x^{-\frac{1}{2}})dx$$
$$=\left[ 3x-2 x^{\frac{1}{2}}\right]_{0}^{2}$$
Al evaluar a la expresión usando los límites de integración, tenemos:
$$=\left[ 3(4)-2 (4)^{\frac{1}{2}}\right]-\left[ 3(1)-2 (1)^{\frac{1}{2}}\right]$$
Finalmente, podemos simplificar considerando que el exponente $latex \frac{1}{2}$ es equivalente a la raíz cuadrada:
$$=\left[ 3(4)-2 (4)^{\frac{1}{2}}\right]-\left[ 3(1)-2 (1)^{\frac{1}{2}}\right]$$
$$=[ 12-4]-\left[ 3-2\right]$$
$latex =8-1$
$latex =7$
EJERCICIO 9
¿Cuál es el valor de la integral $latex \int_{\frac{1}{2}}^{1} 1+\frac{1}{x^2} dx$?
Solución
Reescribimos a los exponentes usando las leyes de exponentes y encontramos la integral de la expresión:
$$\int_{\frac{1}{2}}^{1} 1+\frac{1}{x^2} dx=\int_{\frac{1}{2}}^{1} 1+x^{-2} dx$$
$$=\left[x-x^{-1} \right]_{\frac{1}{2}}^{1}$$
Ahora, evaluamos a la expresión obtenida usando los límites de integración:
$$=\left[1-(1)^{-1} \right]-\left[\frac{1}{2}-(\frac{1}{2})^{-1} \right]$$
Al simplificar, podemos obtener un único valor:
$$=\left[1-1 \right]-\left[\frac{1}{2}-2 \right]$$
$$=-\left[\frac{1}{2}-2 \right]$$
$$=\frac{3}{2}$$
EJERCICIO 10
Resuelve la integral definida $latex \int_{1}^{8} \sqrt[3]{x} dx$.
Solución
Vamos a encontrar la integral de la expresión al escribir a la raíz cúbica como un exponente numérico:
$$\int_{1}^{8} \sqrt[3]{x} dx=\int_{1}^{8} x^{\frac{1}{3}} dx$$
$$=\left[\frac{3}{4}x^{\frac{4}{3}} \right]_{1}^{8}$$
Evaluando los límites de integración, tenemos:
$$=\left[\frac{3}{4}(8)^{\frac{4}{3}} \right]-\left[\frac{3}{4}(1)^{\frac{4}{3}} \right]$$
Podemos simplificar esto al considerar que el exponente $latex \frac{4}{3}$ es equivalente a sacar la raíz cúbica del número y elevar el resultado a la cuarta:
$$=\left[\frac{3}{4}(16) \right]-\left[\frac{3}{4}(1) \right]$$
$$=12-\frac{3}{4}$$
$$=\frac{45}{4}=11~\frac{1}{4}$$
Ejercicios de integrales definidas para resolver
Encuentra el resultado de la siguiente integral definida: $$\int_{1}^{4} 4x^3-6x^2+x^{-\frac{1}{2}} dx$$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
